Soutenons l’utilisation des doigts en maths

Utiliser ses doigts pour calculer après le CP ? Hérésie ! Et pourtant… Les auteurs font le point des recherches sur la question et proposent un dispositif adapté à des élèves présentant une déficience intellectuelle.

Benoît Bonnet, Nathalie Bonneton-Botté, Hélène Hili, Sonia Jarry, Claire Labesse, Fanny Ollivier, Nolwenn Quelaudren & Nadège Saliot

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Introduction

L’utilisation des doigts a toujours été une préoccupation des enseignants et des enseignants spécialisés. Il est en effet observé une incapacité de certains élèves à s’en servir ; certains élèves de CP, par exemple, ne se représentent pas correctement leur main. Parfois, ils ne peuvent pas dire que leur main a 5 doigts sans la regarder et compter leurs doigts. De même, si on leur demande de faire 3 avec une main et 4 avec l’autre main, ils n’y arrivent pas directement car ils sont obligés de tenir avec l’autre main les doigts pliés de la main « qui fait 3 » ou montrent la même quantité sur les deux mains. Ces élèves sont très souvent repérés par les enseignants comme étant en difficulté dans l’utilisation du nombre. La capacité à représenter ses doigts et à les mobiliser impacte ainsi potentiellement le recours à l’utilisation des doigts en situation mathématique.

Améliorer les apprentissages de base en mathématiques et réduire les écarts entre les élèves dans l’école inclusive sont des enjeux de société cruciaux. Par conséquent, le rôle des doigts dans les apprentissages mathématiques se pose à la fois sous l’angle de leur utilité et des apprentissages inhérents à cette utilisation. Ainsi, cette recherche a pour objectif de déterminer l’efficience de l’utilisation des doigts en situation mathématique ainsi que celle d’un dispositif pédagogique d’enseignement explicite de l’utilisation des doigts chez les élèves présentant une déficience intellectuelle.

Nous allons dans un premier temps exposer les éléments théoriques qui ont guidé notre travail ; nous nous centrerons ensuite sur notre recherche participative menée par des chercheuses en psychologie, une formatrice en mathématiques, une conseillère pédagogique de circonscription et des enseignants spécialisés, en apportant un éclairage particulier sur certaines situations de notre dispositif.

Utilisation des doigts en mathématiques

Des tensions existent entre le point de vue de la neurocognition et le point de vue de la didactique des mathématiques sur l’utilisation des doigts [1]. Ces deux disciplines convergent sur le rôle des doigts aux prémices de la construction du nombre mais divergent encore sur leur utilisation à long terme. En didactique des mathématiques, il est avancé la nécessité d’abandonner au plus tôt les stratégies basées sur les doigts dans le comptage et le calcul pour favoriser des représentations symboliques sur lesquelles le calcul va s’appuyer. Mais des études en neurocognition ont mis en évidence que l’usage des doigts apporte un bénéfice aux enfants comme aux adultes, indépendamment de leur niveau de maîtrise mathématique [1]. En effet, pour soutenir un calcul comme par exemple, le traitement d’une multiplication posée, le fait de maintenir ses retenues sur la main qui n’écrit pas est assez pratique pour alléger la mémoire de travail.

Le recours aux doigts est aujourd’hui reconnu comme déterminant dans la construction des premières habiletés de calcul [2, 3]. L’utilisation des doigts permettrait au jeune enfant de représenter les quantités de façon analogique avant que les représentations symboliques ne soient disponibles et d’effectuer des calculs sur ces représentations [4].

Dans une perspective d’apprentissage, en situation de scolarisation inclusive, il est intéressant de prendre en compte un certain nombre d’études qui pointent diverses utilisations des doigts en distinguant différents profils d’élèves. Jordan, Kaplan, Ramineni et Locuniak [5] ont montré que, avant 6 ans, les enfants qui utilisent le plus souvent les doigts pour calculer sont ceux qui effectuent le mieux les tâches arithmétiques. Ils ont étudié les trajectoires développementales du recours aux doigts au cours de tâches de calcul de la maternelle à la fin de la deuxième année d’école élémentaire chez des enfants issus de milieux socio-économiques faibles ou moyens. Les résultats montrent une association entre réussite en calcul et milieux socio-économiques, mais également entre utilisation des doigts et milieux socio-économiques. Les enfants de maternelle issus de milieux à faibles revenus n’utilisent presque jamais leurs doigts spontanément contrairement aux enfants issus de milieux à revenus moyens. En outre, les enfants issus de milieux à faibles revenus commencent à utiliser leurs doigts quand cette stratégie diminue progressivement chez les enfants issus de milieux à revenus moyens et montrent des stratégies moins élaborées que leurs pairs. Plus récemment, Dupont-Boime et Thevenot [6] ont également montré que les enfants suisses romands âgés de 5 à 6 ans qui comptent sur leurs doigts réussissent mieux une tâche d’addition que les enfants qui ne le font pas.

Utilisation des doigts en mathématiques dans l’école inclusive aux cycles 1 et 2

Depuis 2015, l’usage des doigts est mentionné dans les programmes. Dans le programme de cycle 1 [7] au domaine « Acquérir les premiers outils mathématiques », il est mentionné : « Entre deux et quatre ans, stabiliser la connaissance des petits nombres (jusqu’à cinq) demande des activités nombreuses et variées portant sur la décomposition et recomposition des petites quantités […], la reconnaissance et l’observation des constellations du dé, la reconnaissance et l’expression d’une quantité avec les doigts de la main, la correspondance terme à terme avec une collection de cardinal connu. Ultérieurement, au-delà de cinq, la même attention doit être portée à l’élaboration progressive des quantités. »

On retrouve le rôle des doigts dans le programme en cycle 2 [8] dans la partie « Nommer, écrire, représenter des nombres entiers » où il est spécifié : « Utiliser diverses représentations des nombres (écritures en chiffres et en lettres, noms à l’oral, graduations sur une demi-droite, constellations sur des dés, doigts de la main…). »

Dans le guide Pour enseigner les nombres, le calcul et la résolution de problème au CP [9], l’utilisation des doigts lors d’un décomptage est décrite, appuyant ainsi son intérêt.

Cela dit, sur l’ensemble des documents institutionnels, l’apprentissage de l’utilisation des doigts lui-même n’est pas explicité et il n’est pas fait mention des élèves avec trouble du développement intellectuel.

Construire une pratique pédagogique pour des élèves présentant une déficience intellectuelle

L’organisation mondiale de la santé définit la déficience intellectuelle comme la capacité sensiblement réduite de comprendre une information nouvelle ou complexe, et d’apprendre et d’appliquer de nouvelles compétences (trouble de l’intelligence). Il s’ensuit une aptitude diminuée à faire face à toute situation de manière indépendante (trouble du fonctionnement social), un phénomène qui commence avant l’âge adulte et exerce un effet durable sur le développement.

Le dernier rapport produit par l’INSERM [10] en 2016 sur les déficiences intellectuelles (DI) indique que 1 à 2 % de la population française présente une déficience intellectuelle et rappelle que « le fonctionnement et/ou les capacités des personnes avec DI à progresser sont fonction de la présence d’opportunités d’apprentissage et d’un enseignement adapté à leur mode de fonctionnement cognitif ». Les élèves avec DI présentent un retard d’acquisition pour les habiletés numériques (Barrody, 1999), ce qui entrave l’insertion scolaire, sociale et professionnelle. Par conséquent, il existe un vrai enjeu à proposer notamment aux enseignants spécialisés des dispositifs qui peuvent permettre pour des élèves avec DI de démarrer l’apprentissage des premiers nombres avec des outils adaptés ; l’outil qui nous intéresse ici, c’est donc les doigts. Il faut à la fois expliciter l’usage de cet outil et donner les ressources pour l’utiliser.

Expliciter l’usage de l’outil, c’est apprendre à en faire usage dans des situations numériques variées en mettant en avant sa disponibilité et son intérêt en tant que ressource pour appuyer sa pensée.

Donner les ressources pour utiliser l’outil amène à considérer le rôle de la motricité dans les apprentissages.

La motricité aux cycles 1 et 2

La motricité fine correspond à des « petits mouvements musculaires nécessitant une coordination étroite œil-main » [11, p.596].

Quelques études indiquent qu’un entraînement de la motricité fine pourrait améliorer les performances en calcul. Ollivier, Noël, Legrand et Bonneton-Botté [12] ont proposé un entraînement en motricité fine associé à un enseignement explicite de l’usage des doigts et ont observé une augmentation du recours spontané aux doigts en situation de calcul, associé à de meilleures performances en calcul chez des enfants âgés en moyenne de 5 ans.

Des études [13,14] indiquent aussi que le développement de la motricité fine est un facteur facilitant pour le recours aux doigts et que l’enseignement explicite de l’usage des doigts dans le cadre des activités numériques pourrait avoir des effets bénéfiques chez les élèves au développement typique¹.

Ces résultats suggèrent aussi qu’une motricité manuelle insuffisamment développée pourrait constituer une charge cognitive problématique en situation d’apprentissages mathématiques qu’il soit formel ou informel [15]. Fischer et al. [16] recommandent également de soutenir le développement de la motricité fine et d’encourager le recours aux doigts chez les jeunes enfants afin, notamment, de développer les premières habiletés mathématiques.

Les habiletés manuelles n’émergent pas spontanément mais sont le résultat d’apprentissages implicites ou explicites requérant différentes stratégies comme les conduites imitatives ou les répétitions [17]. La recherche d’accessibilité pédagogique inhérente au principe d’une école inclusive conduit à se questionner sur la pertinence de ce type d’intervention pour des élèves à besoin éducatif particulier. Et cela d’autant plus que les enfants avec DI présentent un retard de motricité fine de 3 à 4 ans comparativement à leurs pairs au développement typique [18].

Dans cette étude, nous avons cherché à concevoir et à mettre en œuvre un dispositif d’enseignement à l’usage des doigts à destination d’enfants présentant une déficience intellectuelle légère à modérée. Nos objectifs pour ces élèves avec DI ont été de caractériser le recours spontané aux doigts dans la résolution des problèmes à énoncés verbaux et arithmétiques et ensuite de vérifier si l’entraînement de la motricité et de l’utilisation des doigts en calcul produit un effet similaire à celui observé chez les élèves au développement typique.

Présentation globale du dispositif

Notre groupe de recherche a travaillé à la mise en place d’un dispositif d’enseignement explicite de l’utilisation des doigts dans le cadre d’activités mathématiques. Le dispositif d’enseignement, conçu et expérimenté dans le cadre de cette recherche participative, s’inscrit sur une durée de douze semaines consécutives auprès d’un même groupe d’élèves. Ces séances font l’objet, chaque jour de ces douze semaines, d’une activité ritualisée d’une durée de dix à quinze minutes. Lors de l’expérimentation, la plupart des enseignants ont mis en place ces activités dans leurs classes sous forme d’ateliers.

Les activités proposées relèvent de deux champs d’investigation distincts et interdépendants comme l’ont suggéré Suggate et Stoeger [19, 20]. Le premier champ investi est celui des habiletés manuelles à travers ses diverses composantes que sont l’agilité, la dextérité et la coordination manuelle. Le second champ investi relève de la représentation et de la décomposition des nombres avec les doigts.

Les six premières semaines visent à développer trois compétences distinctes : les habiletés digitales, la représentation mentale de la main et la représentation et décomposition des nombres avec les doigts. La deuxième phase propose une évolution dans le dispositif. En effet, les six dernières semaines donnent lieu à des séances centrées sur la coordination et la dissociation des mains, la coordination main-œil ainsi que la représentation et décomposition des nombres avec les doigts sans feedback visuel et en visant une augmentation de la rapidité.

Pour l’ensemble de cette séquence pédagogique, les principes d’un enseignement qui se veut explicite sont adoptés. Il s’agit d’être transparent auprès des élèves, de leur expliquer pourquoi la motricité et la dextérité sont travaillées ; en effet ces situations peuvent leur paraître à première vue assez éloignées de leurs représentations de situations d’entraînement aux mathématiques. Il s’agit alors d’énoncer au début de chaque séance les objectifs poursuivis par la tâche proposée, de passer par la monstration pour clarifier les gestes et compétences à mobiliser, enfin de resituer la séance dans la séquence en rappelant ou en faisant rappeler les objectifs poursuivis par ces douze semaines de rituels.

Vous trouverez ci-dessous un tableau récapitulant la planification des séquences prévues :

DISPOSITIF PÉDAGOGIQUE

Semaine 1	Semaine 2	Semaine 3	Semaine 4	Semaine 5	Semaine 6	Semaine 7	Semaine 8	Semaine 9	Semaine 10	Semaine 11	Semaine 12
Séquence 1: Muscler, délier pour développer les habiletés digitales et l’agilité						Séquence 4: Dissocier et coordonner les mains
Séquence 2: Se représenter mentalement la main						Séquence 5: Coordonner la main et l’oeil
Séquence 3: Représenter, décomposer le nombre avec les doigts						Séquence 6: Représenter, décomposer le nombre avec les doigts sans feedback visuel et avec rapidité

Apports des enseignants pour la classe

Les coordonnateurs ULIS-école et ULIS-collège de notre groupe de recherche vous proposent maintenant de découvrir certaines situations du dispositif qui relèvent :

de la représentation et décomposition du nombre avec ses doigts (séquence 3) ;
de la musculation et du déliement des doigts (séquence 1) ;
de la coordination main-œil (séquence 5).

Chaque séance commence par un rappel de l’objectif du travail en prenant appui sur le poster :

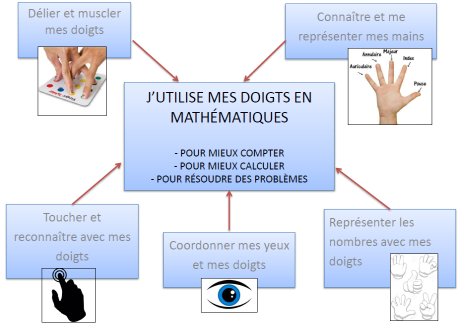
« En apprenant à bien représenter les nombres sur ses doigts, on va pouvoir progresser en calcul mental. »

Activité « Représentation et décomposition du nombre 3 »

L’activité présentée ci-après est une de celles proposées dans la séquence « Représenter et décomposer le nombre avec ses doigts ». Nous allons détailler ici une séance autour du nombre trois ; le même processus a été engagé pour chacun des nombres de un à dix.

Le travail sur un nombre peut, bien sûr, être repris tant que l’enseignant le juge nécessaire.

Les objectifs de la séance
Représenter les nombres de un à dix avec ses doigts de manière « conventionnelle ». Être capable de proposer d’autres représentations des nombres de un à dix avec ses doigts.

Les objectifs de la séance

Représenter les nombres de un à dix avec ses doigts de manière « conventionnelle ».
Être capable de proposer d’autres représentations des nombres de un à dix avec ses doigts.

Le matériel nécessaire à la séance
Le poster « Rappel des objectifs de la séquence » pour le début de la séance. L’affiche de la comptine « Voici ma main » pour le lancement de l’activité. Un appareil photo (ou téléphone portable) pour prendre les photos afin de construire la trace écrite.

Le déroulé de la séance (10-15 minutes) :

Temps 1 : mise en route

La séance débute par la comptine « Voici ma main ».

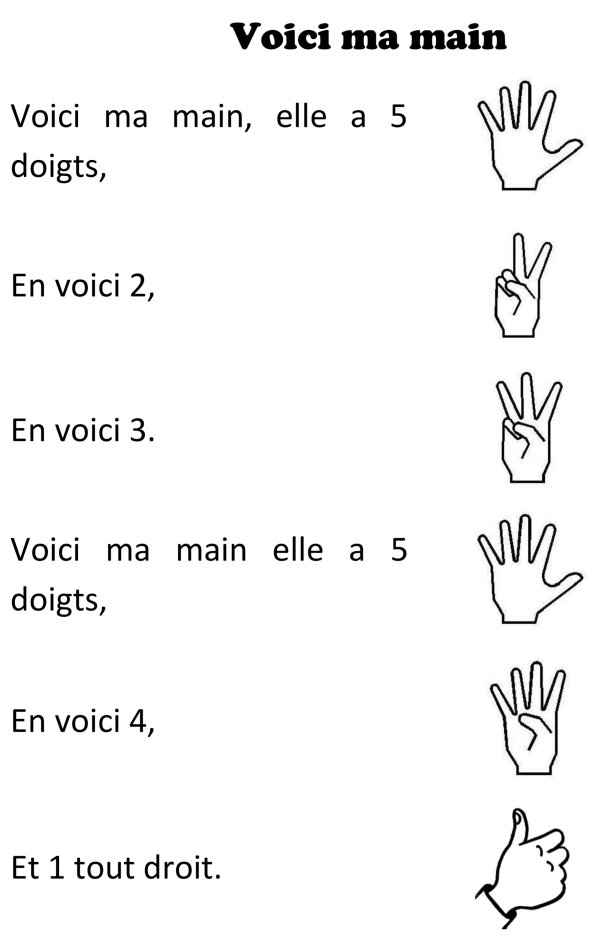
Pour les élèves plus âgés, cette comptine enfantine peut être remplacée par un rappel des représentations des nombres déjà travaillés.

Temps 2 : mobilisation des connaissances

L’enseignant demande aux élèves « de lever 3 doigts ». Très souvent, les élèves lèvent le pouce, l’index et le majeur puisque c’est la représentation conventionnelle du trois dans notre culture et donc à l’école. Ces propositions sont validées par le groupe et les élèves félicités. Les doigts d’un élève sont pris en photo. Dans le cas où la proposition n’est pas juste, l’enseignant demande au groupe de valider ou non. Il faut faire émerger la prise de conscience de l’erreur et la nécessité de reconsidérer le nombre de doigts levés.

Remarque

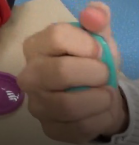
Il est important, pour que l’imprégnation corporelle soit forte, de bien vérifier que les doigts « baissés » le soient très correctement. En effet, parfois cela n’est pas le cas, comme dans cet exemple :

Ici, l’annulaire ne touche pas la paume, par manque de musculation. Parfois les élèves ont besoin d’utiliser l’autre main pour maintenir ces doigts en position pliée. L’enseignant doit être vigilant : les doigts levés doivent être toniques et les doigts baissés collés à la paume de la main.

Sur la photo, il apparaît que l’élève a besoin de muscler, de délier ses doigts. Cela est travaillé à d’autres moments avec d’autres situations, comme celle de « malaxer les balles » ou celle appelée « Les pinces » (proposées dans la suite de cet article).

Temps 3 : recherche élargie

L’enseignant demande alors aux élèves d’autres solutions pour lever 3 doigts. Les mains sont sur les genoux, visibles de l’élève mais invisibles des autres.

Les élèves ont le temps de réfléchir pour sélectionner leurs doigts.

Les élèves montrent alors d’autres propositions. Collectivement chaque proposition est vérifiée et explicitée par les élèves.

Reprise par l’enseignant : « Il y a un doigt, encore un doigt et encore un doigt. Il y a bien 3 doigts ; et tu n’as pas levé le pouce, l’index et le majeur. »

Si l’élève se trompe, son investissement est tout de même valorisé en lui expliquant que sa proposition sera utilisée ultérieurement.

Par exemple si l’élève montre 4 doigts : « Il y a un doigt, encore un doigt, encore un doigt et encore un doigt. Il y a 4 doigts. Garde cette solution en mémoire car bientôt c’est le 4 qui sera travaillé. »

Chaque solution correcte et différente est prise en photo. Cette situation est reprise tant que les élèves ont des idées.

Remarque

Les élèves sont encouragés à utiliser la main non dominante s’ils ne le font pas. De même, les solutions à deux mains sont encouragées si elles ne viennent pas spontanément.

Temps 4 : conclusion / trace écrite

En fin de séance, les solutions trouvées par le groupe sont reprises puis complétées d’une séance à l’autre tant qu’il y a de nouvelles solutions.

Grâce aux photos prises, un affichage est proposé au début de la séance suivante pour rappeler les solutions trouvées. Cet affichage restera en classe dans un espace dédié et constituera la trace écrite ; cet affichage soutiendra la verbalisation des décompositions.

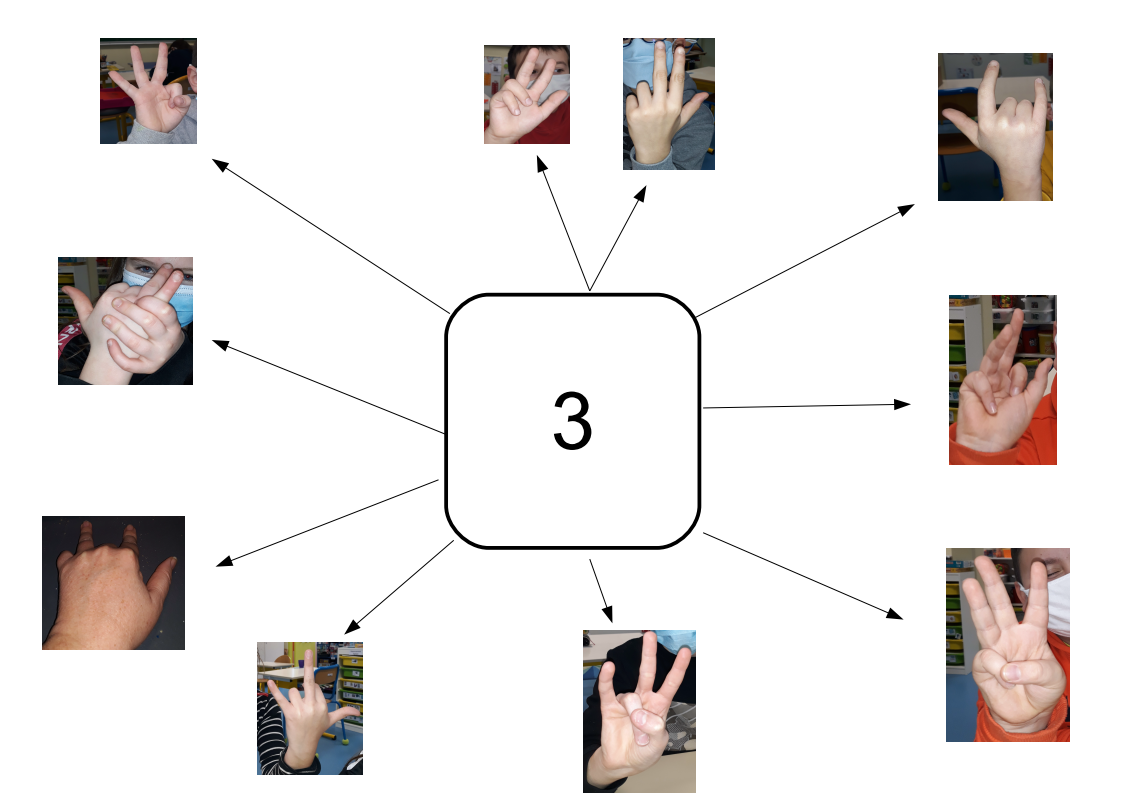
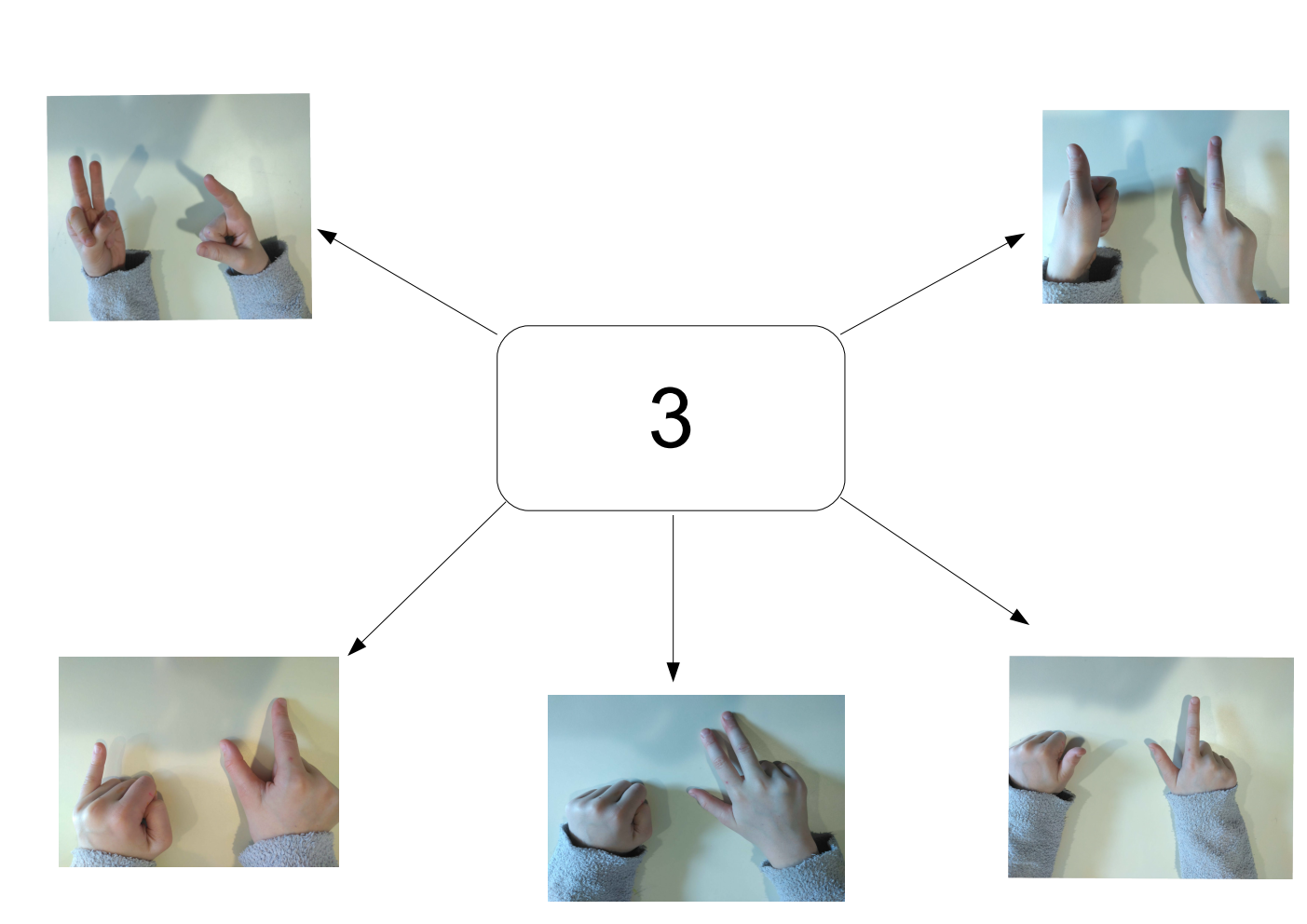
Remarque

Dans la trace écrite, il est intéressant de prendre en photo les mains prises dans les deux sens (côté paume et côté dos). En effet, le côté paume donne davantage d’informations par exemple pour l’apprentissage des compléments à 5 et 10 ; par exemple, si on demande le complément à 5 de 3, on peut lever 3 doigts, et on voit 2 doigts baissés. De plus, l’élève suivant son placement va parfois voir la paume ou le dos des mains de l’enseignant ou d’un autre élève.

Prolongement

Entraîner aussi les élèves à reconnaître le nombre représenté par des doigts levés sous différents angles (dos/paume) : « Combien ai-je de doigts levés ? ».

Activité « Malaxer des balles, de la pâte à modeler »

L’activité présentée ci-après est une de celles proposées dans la séquence « Muscler, délier pour développer les habiletés digitales et l’agilité ».

Les objectifs de la séance
Renforcer la tonicité musculaire des doigts pour les mobiliser plus aisément (main dominante et main non dominante).

Le matériel nécessaire à la séance
Le poster « Rappel des objectifs de la séquence » pour le début de la séance. Des balles de différentes textures. De la pâte à modeler.

Le déroulé de la séance (5 minutes)

Temps 1 : enrôlement

L’enseignant distribue différentes balles (balle farine, anti-stress, en mousse) aux élèves et rappelle le but de l’activité :

« Pourquoi est-ce qu’on va travailler avec des balles ? »

« Pour muscler nos doigts et être plus forts en calcul et en écriture. »

Le poster présenté plus haut est montré.

Temps 2 : mise en route

Il faut être vigilant à bien faire plier les phalanges, à bien saisir la balle par les doigts et non l’écraser dans sa paume.

Il est demandé aux élèves de presser la balle doucement une dizaine de fois, de presser avec l’index seulement, le majeur ensuite, etc.

Les élèves changent de main. Les élèves changent de balle.

Temps 3 : verbalisation des ressentis

Demander aux élèves de parler des ressentis, des sensations quand on presse la balle (« cette balle fait plus mal, là c’est plus mou, etc. ») permet de les centrer sur l’activité et donc de rester actifs dans la tâche.

Remarque

Le fait de ritualiser cette activité permet de faciliter son entrée et permet aussi de faire un brain-break (une pause attentionnelle) suite à des activités plus intenses (comme les temps d’accueil en classe ou les récréations). Les élèves à profil particulier apprécient cette activité tactile et centrée sur leurs sensations qui leur procure de la détente.

Activité « Les pinces »

L’activité présentée ci-après est une de celles proposées dans la séquence « Coordonner la main et l’œil ».

Les objectifs de la séance
Coordonner la main et l’œil. Muscler les doigts.

Le matériel nécessaire à la séance
Le poster « Rappel des objectifs de la séquence » pour le début de la séance. Des bacs. Des pinces diverses (plus ou moins souples, plus ou moins fines ; ex. : pince à épiler, pince à pain grillé, pince double-boule de glace). Divers objets à transvaser (jouer sur les textures, les tailles, les formes). Le tableau de suivi des scores. Un chronomètre. Une ardoise.

Remarque

Ces différents types de matériel obligent des prises en main différentes et donc des actions motrices manuelles différentes.

Le déroulé de la séance (10 minutes)

Temps 1 : enrôlement

Il est expliqué (ou on fait expliciter aux élèves) l’activité :

« Pourquoi est-ce qu’on travaille avec les pinces ? »
« Pour mieux maîtriser nos doigts. »

Le poster présenté plus haut est montré.

Temps 2 : mise en route des ateliers

Différents ateliers sont proposés aux élèves avec différentes pinces et/ou différents objets à transvaser d’un bac à l’autre.

Il est demandé de déménager d’un bac à un autre le maximum d’objets un par un pendant 30 secondes (chronomètre). Quand un objet tombe à côté d’un bac pendant le transvasement, cet objet est écarté du jeu.

Vue d’ensemble du matériel fourni et le score final par élève sur ardoise.

Temps 3 : relevé des résultats

Les résultats sont notés sur l’ardoise par les élèves eux-mêmes ou par l’enseignant, suivant les possibilités des élèves concernés, à la suite de leur passage dans un des quatre ateliers. Tous ces scores seront répertoriés ensuite dans le tableau de suivi de scores (voir ci-dessus) pour garder trace d’une séance à l’autre et générer de la motivation.

Remarque

La motivation se met en place à la faveur de différents types de challenges : l’élève se met au défi d’une séance à l’autre, d’une main à l’autre, d’un type de pince à l’autre ou bien défie un camarade. Cela permet même aux élèves plus âgés de trouver une motivation à cette activité et de la soutenir. Sur ce type de séance, le temps d’activité peut aller jusqu’à 15 ou 20 minutes en fonction de l’engagement des élèves par rapport au challenge proposé.

Conclusion

Les premières analyses des résultats de l’ensemble du dispositif centré sur la motricité manuelle et l’enseignement explicite conçu dans une démarche coopérative vont dans le sens de nos hypothèses. Le dispositif a permis aux élèves présentant une déficience intellectuelle d’augmenter leurs compétences en mathématiques (nombre, résolution de problèmes, addition lacunaire). Cette amélioration des performances s’accompagne d’une augmentation du recours aux doigts seulement pour les problèmes avec énoncé verbal ; cela est probablement dû à la difficulté de ces élèves à maintenir en mémoire les nombres intervenant dans un problème verbal et alors, les doigts sont probablement là pour un soutien à la mémorisation.

D’un point de vue qualitatif, les élèves se sont engagés dans le dispositif et les enseignants ont perçu cet engagement ; cela peut s’expliquer par deux facteurs : l’ensemble des activités proposées rend les élèves actifs et chaque activité s’accompagne de retours verbaux sur les notions impliquées.

Il importe donc de travailler ce lien entre la motricité fine et les mathématiques dès le cycle 1, en objectivant la démarche par rapport aux mathématiques dans les classes ordinaires, et évidemment dans les dispositifs de type ULIS-école et ULIS-collège où les séances proposées ont été testées. Cette démarche permet de poser un regard nouveau sur l’utilisation des doigts en mathématiques. Elle s’inscrit dans une perspective de mise en accessibilité des apprentissages qui permettra au plus grand nombre d’élèves, grâce à l’utilisation des doigts, d’accéder aux situations mathématiques.

Références

K. Moeller et al. « Effects of Finger Counting on Numerical Development – The Opposing Views of Neurocognition and Mathematics Education ». In : Frontiers in Psychology (2011). .
N. Guedin, C. Thevenot et M. Fayol. « Des doigts et des nombres ». In : Psychologie française, n° 63(4) (2018), p. 379-399.
X. Seron et V. Crollen. « Le comptage sur les doigts comme support au développement des capacités numériques et arithmétiques de base ? ». In : ANAE, n° 156 (2018), p. 531-537.
R. Siegler et J. Shrager. Strategy choices in addition and subtraction: How do children know what to do ? Origins of Cognitive Skills ? 1984.
N.C. Jordan et al. « Development of number combination skill in the early school years: When do fingers help ? ». In : Developmental Science, n° 11(5) (2008), p. 662-668. .
J. Dupont-Boime et C. Thevenot. « High working memory capacity favours the use of finger counting in six-year-old children ». In : Journal of Cognitive Psychology, n° 30(1) (2018), p. 35-42 .
« J’enseigne au cycle 1 ». In : BOEN, n° 25 (24 juin 2021). .
« J’enseigne au cycle 2 ». In : BOEN, n° 31 (30 juillet 2020). .
Le guide « Pour enseigner les nombres, le calcul et la résolution de problèmes au CP ». 2021. .
Inserm. Déficiences intellectuelles. Collection Expertise Collective, 2016.
Z. Luo et al. « Fine motor skills and mathematics achievement in East Asian American and European American kindergartners and first graders ». In : British Journal of Developmental Psychology, n° 25(4) (2007), p. 595-614. .
F. Ollivier et al. « A teacher-implemented intervention program to promote finger use in numerical tasks ». In : European Journal of Psychology of Education, n°35 (2020), p. 589-606. .
N. Bonneton-Botté et al. « Évaluation des bénéfices d’un dispositif d’entraînement à l’usage des doigts en mathématiques. ». In : Canadian Journal of School Psychology, n°37(3) (2022), p. 289-303. .
F. Ollivier et al. « Dynamic Interplay between Fingers and Working Memory in Calculation among Adolescents with Mild Intellectual Disability ». In : Learning Disabilities Research and Practice. (soumis).
F. Bara et A. Tricot. « Le rôle du corps dans les apprentissages symboliques. Apports des théories de la cognition incarnée et de la charge cognitive ». In : Recherches sur la philosophie et le langage, n°33 (2017), p. 219-249.
U. Fischer, S.P. Suggate et H. Stoeger. « The Implicit Contribution of Fine Motor Skills to Mathematical Insight in Early Childhood ». In : Frontiers in Psychology, n°11 (2020). .
J.D. Goodway, H. Crowe et P. Ward. « Effects of Motor Skill Instruction on Fundamental Motor Skill Development ». In : Adapted Physical Activity Quarterly, n°20 (2003), p. 298-314. .
P. Rintala et E.M. Loovis. « Measuring Motor Skills in Finnish Children with Intellectual Disabilities ». In : Perceptual & Motor Skills, n°116(1) (2013), p. 294-303. .
S. Suggate et H. Stoeger. « Fine motor skills enhance lexical processing of embodied vocabulary : A test of the nimble-hands, nimble-minds hypothesis ». In : Quarterly Journal of Experimental Psychology, n°70(10) (2017), p. 2169-2187. .
S. Suggate, H. Stoeger et E. Pufke. « Relations between Playing Activities and Fine Motor Development ». In : Early Child Development and Care, n°187(8) (2017), p. 1297-1310.