Tac Tic Maths
Anne Bouchard et Agnès Veyron enseignent les mathématiques en collège. Toutes deux convaincues de l’importance des rituels et des activités flash, elles sont à l’origine de la création du site Tac Tic Maths hébergé par les éditions Didier. Leur enthousiasme donne envie de le tester avec nos élèves !
Anne Bouchard, Agnès Veyron
© APMEP Septembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Nous pratiquons depuis des années, dans toutes nos classes, des rituels de début de cours constitués d’activités rapides projetées, couramment appelées questions flash. Nous avons constaté qu’entraîner les élèves quotidiennement dans les domaines du calcul mental et du raisonnement permettait d’installer une ambiance de travail sereine et aidait chacun à progresser.
En revanche, la création de diaporamas à modifier chaque année en fonction de la classe, de la progression et du besoin de spiralage est une perte de temps considérable au détriment de la pédagogie !
Nous avons donc retroussé nos manches et avons imaginé un outil permettant de générer rapidement des diaporamas à partir d’une base de plus de 3 000 ressources que nous avons créées.

Nous voulions un outil accessible partout, ergonomique, simple d’utilisation et paramétrable.
Nous avons démarché les éditeurs pour soutenir notre projet. Les éditions Didier nous ont fait confiance et ont accepté de partir à l’aventure avec nous sur le niveau 5e. C’est ainsi qu’est né Tac Tic Maths, site dont nous allons vous présenter toute la richesse.
Pourquoi proposer des activités flash aux élèves
Pour ceux qui ne seraient pas encore convaincus, voici quelques points :
-
Tout d’abord, les élèves aiment ça ! Et le plaisir est une composante importante dans l’acquisition des connaissances.
-
C’est une pratique qui permet de faciliter la gestion de classe. Le diaporama chronométré va commencer, les élèves se dépêchent de s’installer. Ils sont en activité très rapidement. Ils sont mobilisés individuellement dès le début, laissant le temps au professeur de faire l’appel et les vérifications de signatures, de devoirs…
-
Cette pratique convient aux élèves en difficulté. En effet, les élèves pour lesquels le passage à l’écrit est difficile, sont souvent en réussite dans ce type d’activité. Les élèves dyslexiques par exemple sont plus performants à l’oral et se sentent valorisés par ce type de travail. D’autres élèves à besoins éducatifs particuliers ont besoin de rituels sécurisants pour les apprentissages.
-
Ces activités permettent un gain de temps lorsqu’elles sont intégrées de manière réfléchie dans la progression. Elles facilitent les apprentissages spiralés et les acquis sont entretenus tout au long de l’année.
-
C’est un outil didactique intéressant. Pour l’élève, en plus de développer de l’aisance en calcul, il permet de mémoriser, de raisonner et de confronter ses démarches à celles des autres. Le professeur peut l’utiliser pour faire des évaluations diagnostiques, pour diversifier les approches en proposant par exemple des changements de cadre ou pour différencier son enseignement.

Qu’est-ce qu’une série d’activités flash dans Tac Tic Maths
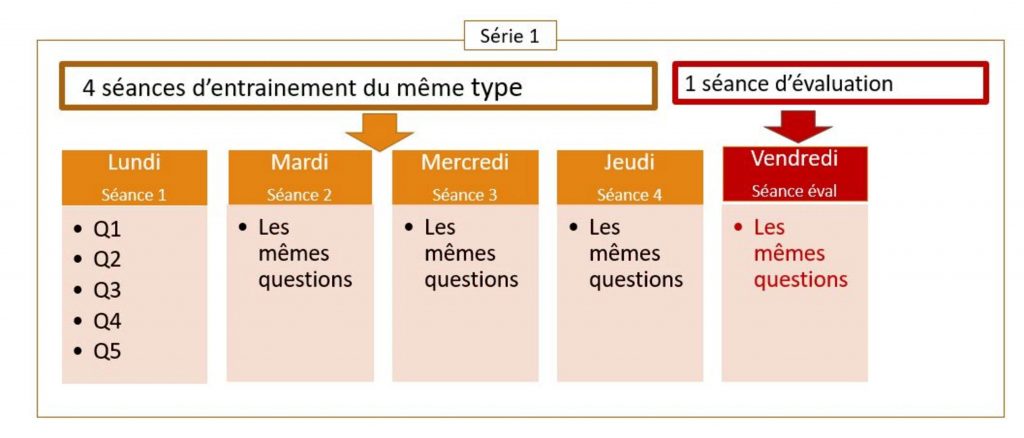
Ce site permet de générer automatiquement une série composée de séances, elles-mêmes composées de questions. En pratique, nous proposons à nos élèves un maximum de 5 séances d’entraînement consécutives de même structure, puis une séance d’évaluation.
La structure des activités flash laisse le temps aux élèves de s’approprier l’énoncé à leur rythme : certains dès la première séance, d’autres au bout de la 2e ou 3e séance. La séance d’évaluation peut s’afficher avec un sujet A et un sujet B.
Les questions défilent une à une chronométrées. Les énoncés peuvent être imprimés et distribués aux élèves ou mis à disposition sur l’ENT.
Séance 1
|
Séance 2
|
Les types de questions proposés par Tac Tic Maths
Les activités flash, c’est bien sûr le calcul mental traditionnel : les tables de multiplication, les multiplications et divisions par \(10\), \(100\), \(1\,000\), les additions de nombres entiers du type \(28 + 9\)… Mais Tac Tic Maths propose aussi d’autres types de questions.
Du calcul réfléchi
Exemple 1 :
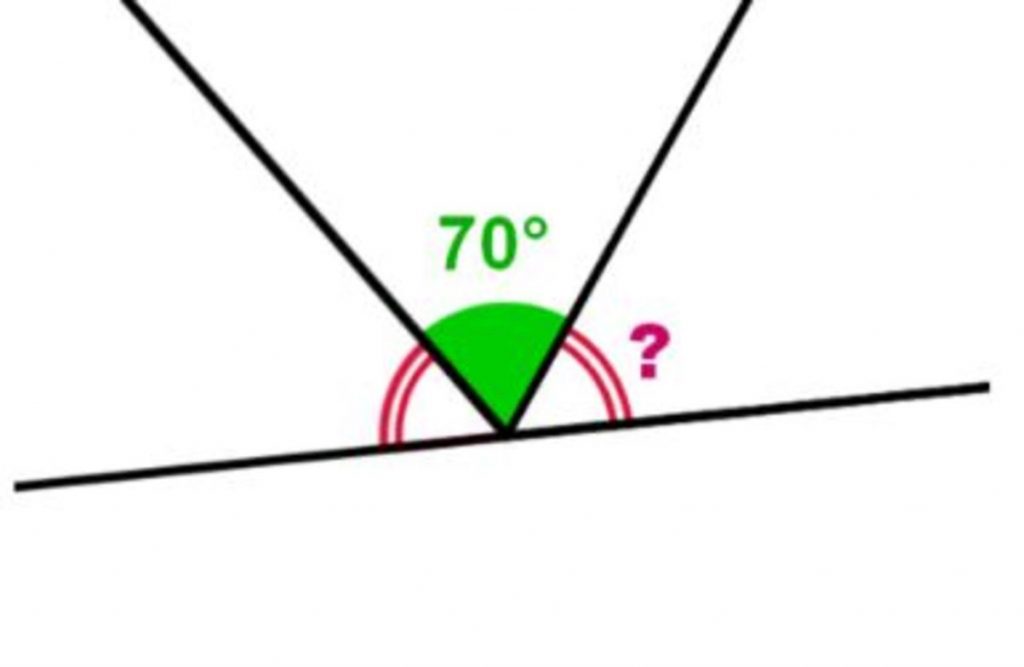
l’angle plat mesure 180°, deux angles codés de la même façon sont égaux, on le sait et puis on l’oublie. D’où l’intérêt de proposer des questions faisant appel à ces savoirs géométriques afin de les mobiliser régulièrement.
Exemple 2 :
|
Calcule astucieusement : \[\mathsf{13}\times\mathsf{8}\] |
\(13\) multiplié par \(8\), c’est \(13\) multiplié par \(10\) moins \(13\) fois \(2\). L’utilisation de la distributivité en acte permet de développer une aisance en calcul mental, mais aussi permet de donner corps à cette propriété. L’appropriation de celle-ci sera alors plus facile, lorsqu’il s’agira de l’expliciter.
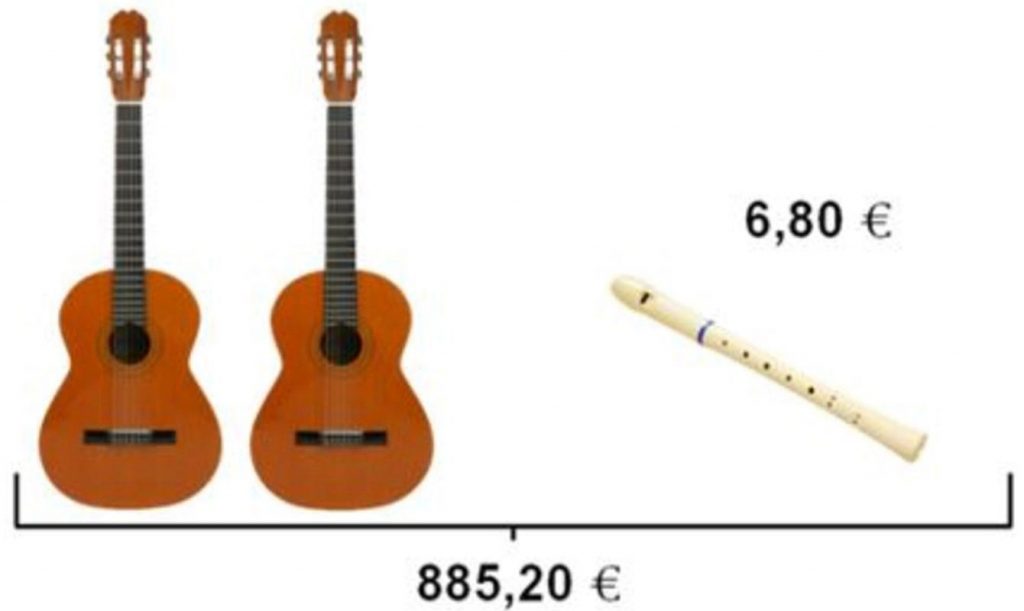
Exemple 3 : Monter en performance dans un domaine. Calculer \(10\) %, \(20\) %, \(30\) % puis \(1\) %, \(2\) %, \(4\) % d’une quantité jusqu’à arriver en fin d’année au calcul de \(27\) % par combinaison, ceci dans un temps raisonnable.
|
Calcule le montant de la réduction.
|
Du calcul instrumenté
C’est l’occasion bien sûr d’apprendre à se servir des fonctions de la calculatrice, de travailler sur les ordres de grandeurs, les valeurs approchées. Cependant l’usage de la calculatrice en activité flash présente aussi d’autres avantages.
Exemple :
|
Calcule : \[\mathsf{2}x+\mathsf{3}\text{ pour }x=\mathsf{6}\] |
Dans cet exemple, il est nécessaire d’appuyer sur la touche \(\times\) de multiplication de la calculatrice, cela permet d’apprendre à lire une expression littérale. Dans un autre ordre d’idée, utiliser la calculatrice pour résoudre un problème permet de se concentrer sur le choix de l’opération à effectuer.
Des questions « Tableur en débranché »
Vous avez fait une séance en salle informatique pour travailler sur tableur. Chacun a travaillé sur son poste, la mise en commun en salle informatique n’est pas toujours aisée. Vous n’êtes pas sûr(e) de l’efficacité des méthodes de travail des élèves et donc de leurs apprentissages : ont-ils écrit les formules ou cliqué sur les cases et utilisé la complétion ? Ont-ils demandé à un camarade de les débloquer ? Il est donc pertinent de proposer des exercices en débranché pour la mise en commun et l’explicitation des procédures : l’adressage, les opérations.
Exemple :
|
Quel résultat obtient-on dans la cellule C1 en appuyant sur « Entrée » ?
|
Des questions de cours pour revenir sur l’apprentissage du vocabulaire et des propriétés
Il est important de revenir régulièrement sur l’apprentissage du vocabulaire et des propriétés.
Exemple 1 :
|
L’expression \((\mathsf{15}-\mathsf{11})\times\mathsf{9}\) est : A) une somme B) une différence C) un produit |
Exemple 2 :
|
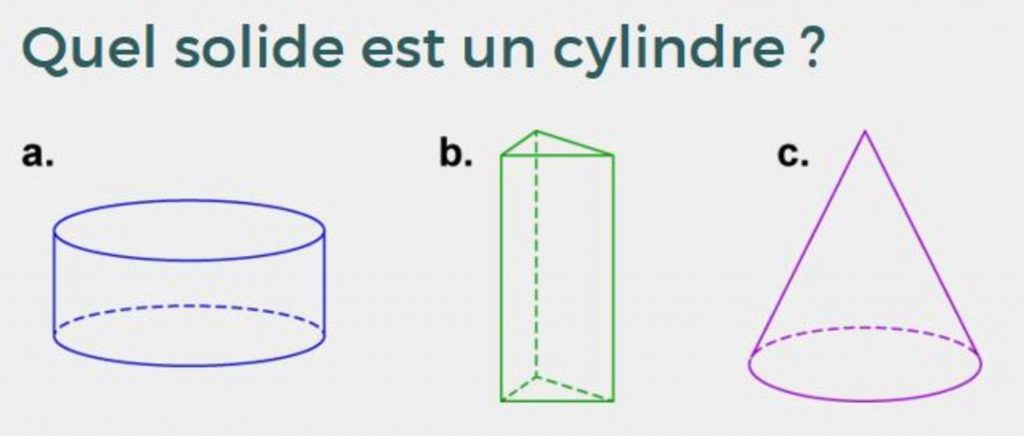
Quel solide est un cylindre ?
|
Des questions de vocabulaire
Moins que, moins de, au moins, \(x\) fois moins… La différence entre ces expressions n’est pas simple à faire.
Exemple 1 :
|
\(\mathsf{4}\) fois moins que \(\mathsf{44}\) est égal à : A) \(\mathsf{11}\) B) \(\mathsf{40}\) C) au quadruple de \(\mathsf{44}\) D) \(\mathsf{176}\) |
En posant une question par jour, on peut se demander ce qui la distingue de celle de la veille, à quelle phrase correspondent les réponses incorrectes. Ces questions permettent de s’approprier petit à petit ce vocabulaire.
De même, on s’interroge sur les mots : toujours, parfois, jamais. Que veulent-ils dire ?
Exemple 2 :
|
Deux droites symétriques par rapport à une droite ne sont jamais parallèles A) Vrai B) Faux |
À travers ces questions se mettent en place les notions de propriété, d’exemple et de contre-exemple.
Des séries de problèmes
Il peut être bien d’entraîner les élèves à dégager des classes de problème.
Exemple 1 :
|
Maxime a \(\mathsf{24}\) porte-clés. Il souhaite en donner le même nombre à chacun de ses invités. Combien peut-il inviter de personnes ? |
Dans cet exemple, cherche-t-on les multiples ou les diviseurs de \(24\) ?
Il est intéressant de poser des questions qui peuvent susciter un débat en classe.
Exemple 2 :
|
La masse d’un cageot de melons est-elle proportionnelle au nombre de melons ? |
Oui, non, pourquoi ? Les représentations des élèves sur la proportionnalité se mettent à jour à cette occasion. Il est judicieux de placer ces questions en dernière position de la série et il n’est pas forcement pertinent de garder ce type de question pour l’évaluation, les réponses étant, par nature, sujettes au débat.
Des questions pour prendre des initiatives, utiliser une stratégie
Exemple :
|
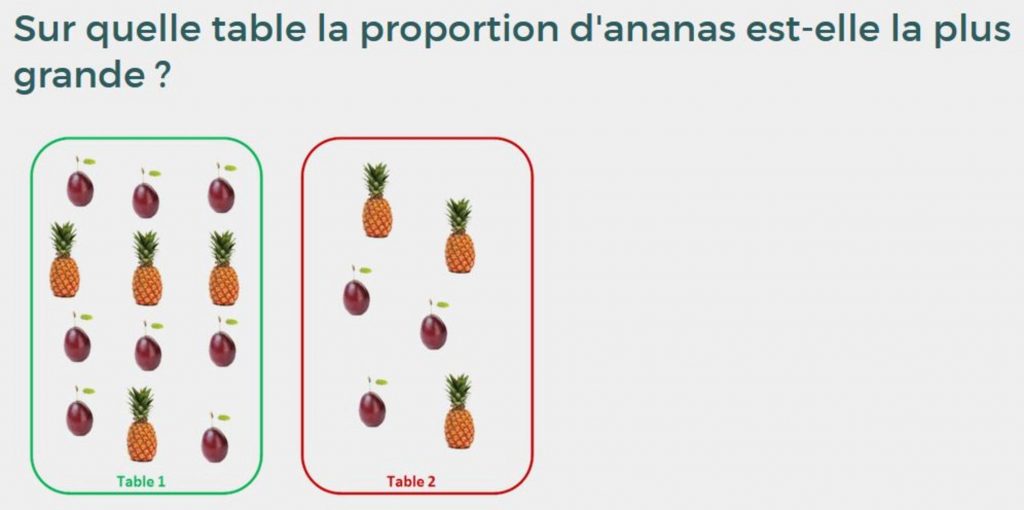
Sur quelle table la proportion d’ananas est-elle la plus grande ?
|
Comparer à la moitié, au tiers, ramener au même nombre de fruits, d’ananas, faire des groupes… La stratégie utilisée à la séance précédente fonctionne-t-elle encore pour cette séance ? Y a-t-il une stratégie qui permet de conclure quel que soit le nombre de fruits posés sur les tables ? L’ensemble de toutes ces questions permet d’interroger en profondeur la notion de proportion.
Exemples de séquences intégrant des activités flash
Les activités flash permettent d’approcher une notion, de stabiliser un apprentissage, de réinterroger des connaissances. Elles sont donc présentes tout au long de l’apprentissage en cohérence avec les séquences de cours.
Voici un exemple d’articulation des activités flash avec les séquences d’apprentissage sur les nombres relatifs en classe de 5e. Notre progression est la suivante :
Séquence 1 : découverte des nombres relatifs et de leur usage en termes de repérage ; notion de droite graduée et de repère
Pendant la première séquence : il est difficile de travailler la notion en amont donc, dans ce cas, les premières activités flash prennent leur place juste après la mise en évidence de l’existence des nombres négatifs. On commence par des lectures de graduation de thermomètre, d’abscisse de point.
Exemples :
|
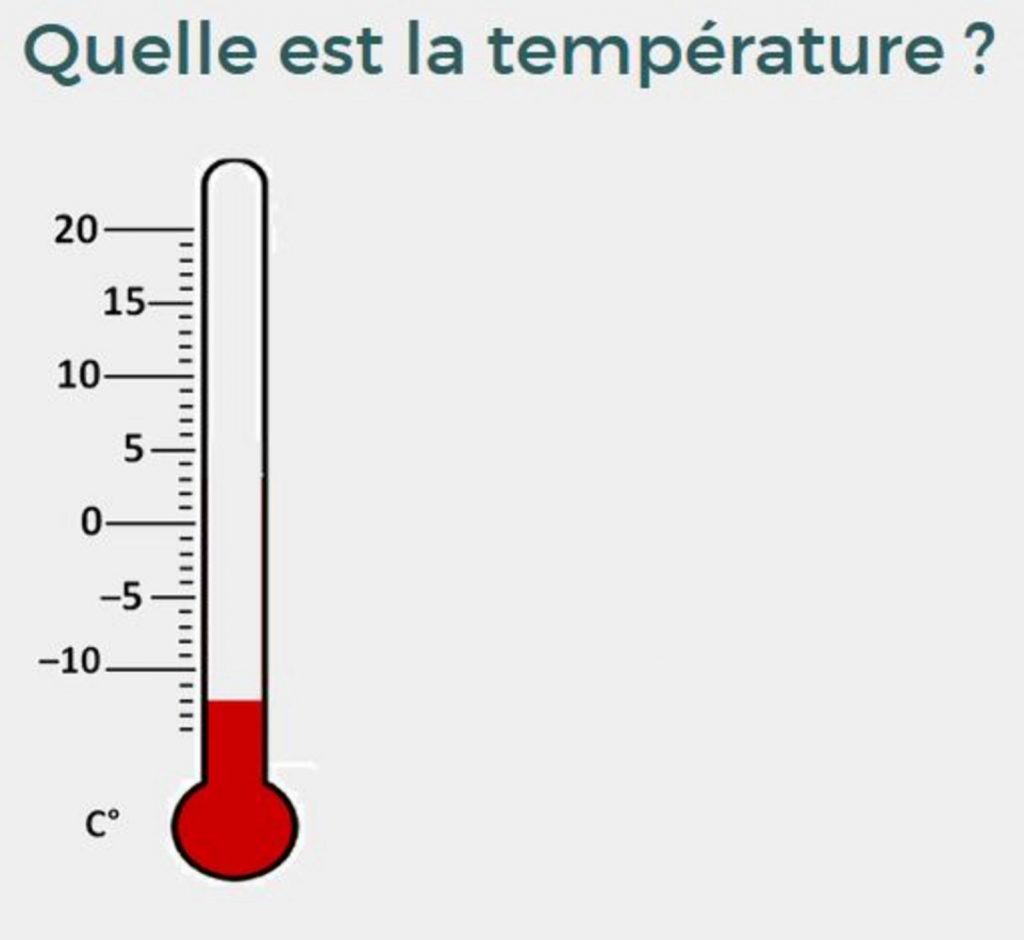
Quelle est la température ?
|
|
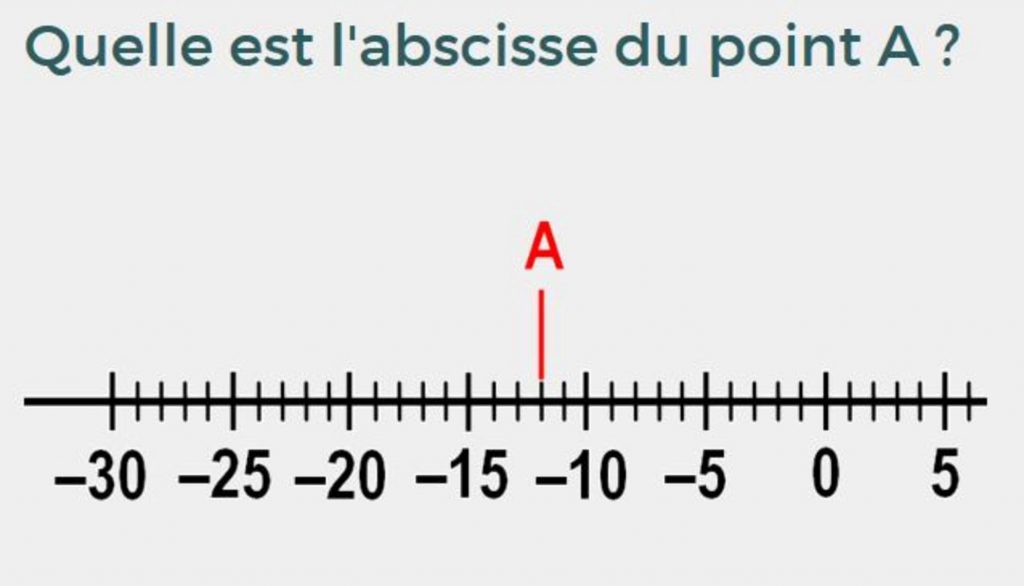
Quelle est l’abscisse du point A ?
|
L’idée est de mettre à la vue de l’élève à chaque début d’heure, cette droite graduée dotée d’un sens croissant : de la gauche vers la droite, du bas vers le haut et de créer ainsi, jour après jour une image mentale associée à un discours de gauche à droite, des nombres les plus petits vers les plus grands.Puis viennent les questions de repérage dans le plan associées au vocabulaire abscisse et ordonnée.
Questions simples :
|
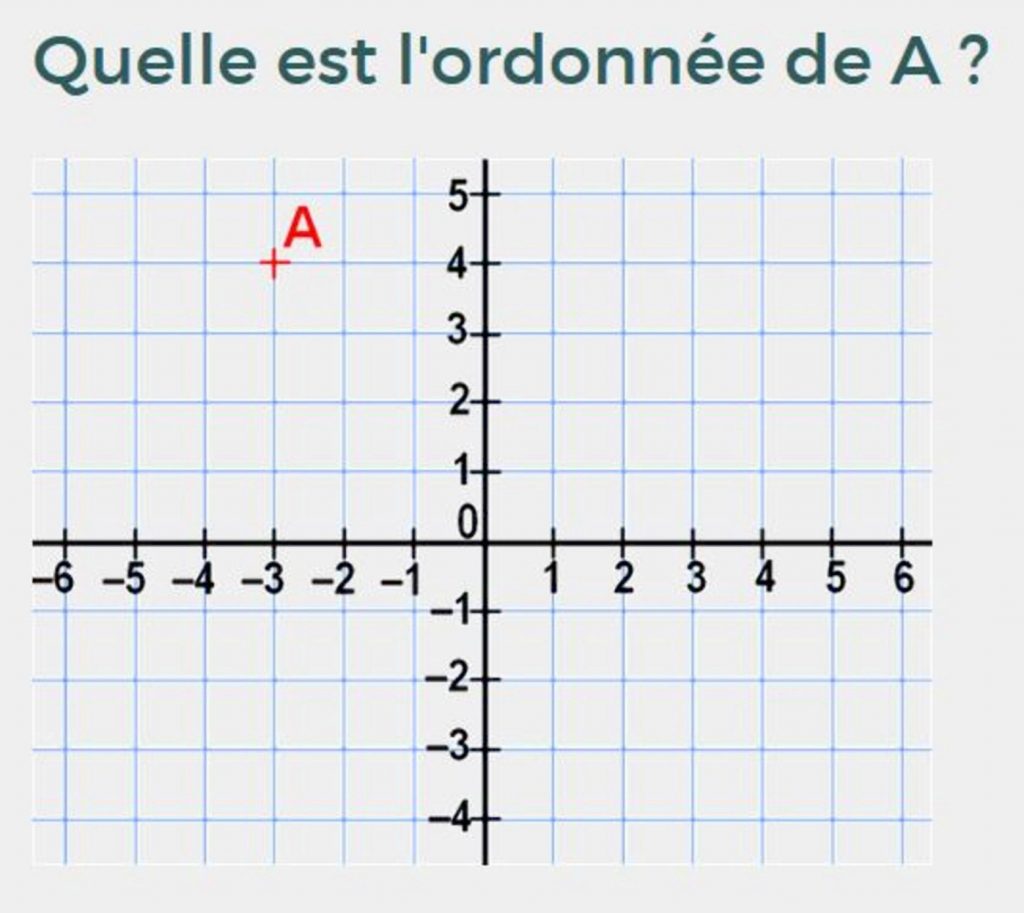
Quelle est l’ordonnée de A ?
|
puis demandant un peu plus de réflexion :
|
Qui suis-je ?
|
Après la première séquence sur les nombres relatifs et avant d’aborder les additions, il est intéressant d’éprouver, d’interroger cette première représentation des nombres relatifs construite par les élèves.
C’est le temps des questions du type :
|
Les nombres négatifs sont tous plus petits que \(\mathsf{0}\). A) Vrai B) Faux |
D’autre part, la droite numérique est construite, profitons-en pour se promener dessus, comptons, décomptons, parcourons-la de gauche à droite, de droite à gauche, pas à pas, en sautant de \(2\) en \(2\), de \(3\) en \(3\)…
|
Compte de \(\mathsf{2}\) en \(\mathsf{2}\) : \(-\mathsf{85}\longrightarrow\ldots\longrightarrow\ldots\longrightarrow\ldots\) |
|
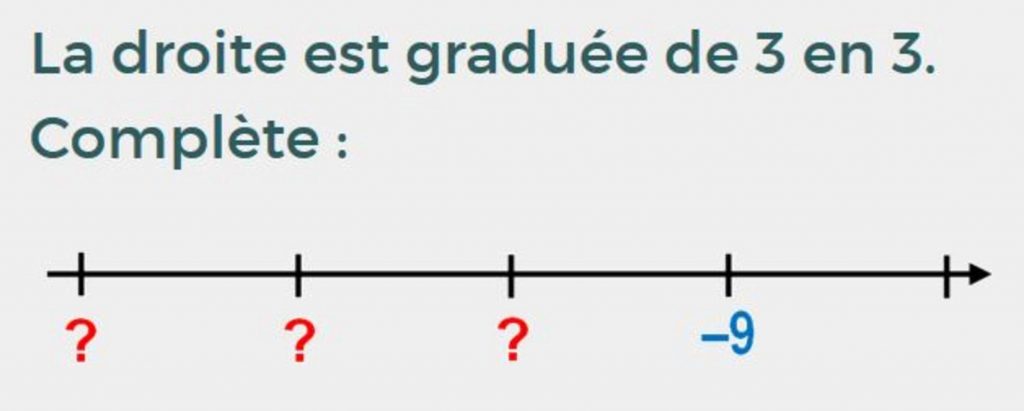
La droite est graduée de 3 en 3.
|
Les procédures sont bien des procédures de comptage et décomptage mais pas encore d’addition ou de soustraction. Mais cette appropriation, cette familiarisation avec la droite graduée va permettre un apprentissage des opérations plus rapide et plus efficace.
Séquence 2 : addition de nombres relatifs
Pour introduire les opérations, nous utilisons le modèle des déplacements.
Pendant la séquence 2, nous traitons les additions de relatifs avec un support numérique quasi-exclusivement (voir par exemple le site d’Agnès Veyron ![]() ) et sommes donc face à un problème de mise en commun et d’institutionnalisation.
) et sommes donc face à un problème de mise en commun et d’institutionnalisation.
Les questions flash permettent d’assurer ce travail avec des additions de nombres relatifs, des questions du type :
|
Le résultat est-il positif ou négatif ? \[\mathsf{5}+(-\mathsf{7})\] |
Ces questions sont l’occasion de discuter en grand groupe des procédures mises en œuvre par chacun devant son écran.
Entre l’addition et la soustraction : les questions flash entretiennent les additions de relatifs.
D’abord avec des questions dont le résultat est accessible visuellement :
|
Calcule : \[-\mathsf{4}+(-\mathsf{4})\] |
Avec la possibilité d’afficher une aide :

Puis des questions dont le résultat est accessible en comptant :
|
Calcule : \[\mathsf{44}+(-\mathsf{7})\] |
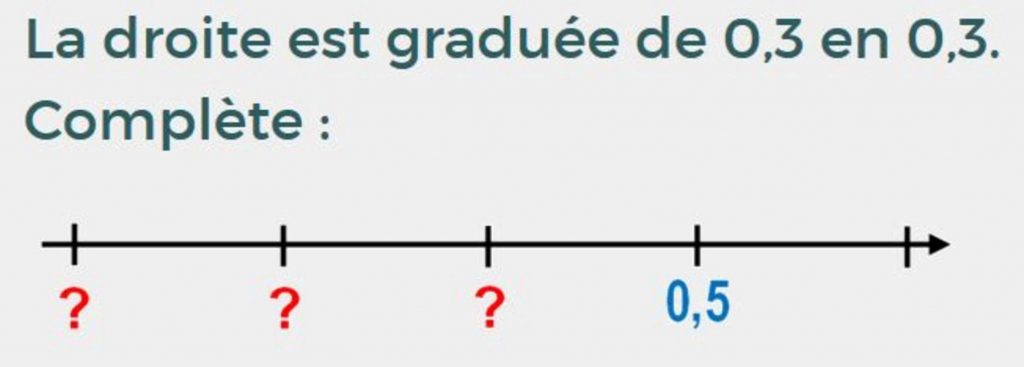
D’autre part, nous posons encore et toujours des questions de comptage et décomptage, avec des nombres décimaux cette fois.
|
La droite est graduée de 3 en 3.
|
Séquence 3 : la soustraction de nombres relatifs
Cette séquence se traite également avec support numérique. Les questions flash sont constituées de soustractions simples, de questions QCM du type :
|
Calcule : \[-\mathsf{83}+\mathsf{49}\] A) \(-\mathsf{132}\) B) \(-\mathsf{34}\) C) \(\mathsf{34}\) D) \(\mathsf{132}\) |
Ceci afin de pouvoir, au moment de la correction avec la classe, mettre en évidence les stratégies de calcul et les moyens de contrôle des erreurs.
Après la découverte des opérations, suit un temps de mise à distance du modèle des déplacements, durant lequel l’élève apprend à développer des stratégies plus performantes que de visualiser l’intégralité du déplacement sur la droite ou d’utiliser son corps pour mimer ces déplacements.
C’est à l’issue de cette phase de mise à distance du modèle que l’élève pourra être compétent sur les additions et soustractions de relatifs. Les activités flash l’accompagnent sous forme de questions d’addition et de soustraction nécessitant la mise en place d’une procédure opératoire, l’élève ne peut plus se contenter de compter :
|
Calcule : \[\mathsf{37}-(-\mathsf{38})\] |
Séquence 4 : les sommes algébriques
À la fin de l’année de 5e, une fois les additions et soustractions mises à distance du modèle qui a servi à les introduire, on peut alors aborder les sommes algébriques, et continuer à les mobiliser jusqu’à la fin de l’année.
|
Calcule : \[-\mathsf{5}-(-\mathsf{4})+(-\mathsf{6})+\mathsf{2}\] |
Les plus de Tac Tic Maths
-
La facilité d’utilisation : on peut créer en 5 minutes une série d’activités flash pour la semaine, adaptée à sa classe et à sa progression. Ou bien choisir d’utiliser les parcours déjà prêts en modifiant éventuellement quelques questions.
-
La diversité et la richesse des ressources : plus de 3000 questions couvrant tout le programme de 5e produites à l’issue de quinze ans de pratique et de recherche didactique.
-
L’adaptation aux différentes pratiques : presque toutes les questions sont proposées sous forme de QCM pour ceux qui ont des boîtiers de réponses ou Plickers.
-
Le site propose des évaluations avec simple ou double énoncé au choix. Il propose également une correction de chaque question.
-
La diversité des utilisations : accessible depuis tout navigateur internet, on peut exporter une série pour pouvoir l’utiliser localement sur un ordinateur sans connexion internet. Le site génère un PDF que l’on peut imprimer ou mettre à disposition des élèves via l’ENT. Ainsi les élèves peuvent revoir les séances avant l’évaluation ou bien préparer en amont une séance.
-
La différenciation : pour certaines questions, on peut choisir des aides didactiques affichables à l’énoncé et des aides visuelles à la correction facilitant ainsi la mise en commun de différentes procédures. On peut aussi proposer des questions dont le niveau de la réponse peut varier.
-
La possibilité de paramétrage : la structure même de la série est modifiable. Toutes les séances identiques avec les mêmes premières questions, les mêmes deuxièmes questions… ou bien inversement des séances homogènes mais chaque jour différentes. Sont modifiables également le temps d’affichage de la question, le nombre de séances, le nombre de questions, le choix de QCM ou encore l’affichage des aides.
-
L’accompagnement du professeur : les objectifs didactiques sont précisés. Les questions sont classées : réactivation de connaissances, approche d’une nouvelle notion, entraînement et réinvestissement d’une notion. Enfin, on trouve des parcours clé en main, pensés suivant une progression, qui sont modifiables.
Aspects pratiques
La licence Tac Tic Maths individuelle enseignant coûte 50 €. Mais bonne nouvelle : elle est à 25 € pour tous les adhérents de l’APMEP et pour ceux qui utilisent le manuel Mathsmonde cycle 4 (Didier)1.
La licence établissement Tac Tic Maths est à 50 € pour 10 postes.
Le lien pour la commande en ligne est : ![]() .
.
Référence
-
IREM de Clermont-Ferrand. Activités mentales — Automatismes au collège. APMEP n° 191, 2010.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Anne Bouchard et Agnès Veyron enseignent respectivement au CMPA (Centre Médical et Pédagogique pour Adolescents) de Neufmoutiers-en-Brie et au collège de Champagne Sur Seine. Si vous souhaitez avoir plus d’informations sur Tac Tic Maths, vous pouvez leur adresser directement un courriel :
-
Les ressources pour les niveaux 4e et 3e sont produites, il n’y a pas encore de date précise de parution mais nous espérons qu’elles seront disponibles rapidement. ↩





Une réflexion sur « Tac Tic Maths »
Les commentaires sont fermés.