Transformations littérales et manipulations
en Quatrième

Comprendre les techniques de calcul avec des écritures littérales n’est pas simple pour la majorité de nos élèves. Nombre d’entre nous aimeraient trouver une activité qui peut les aider à appréhender ces savoir-faire. Morgan Gilot nous propose dans cet article des manipulations qui ont permis à certains de ses élèves de s’approprier quelques transformations littérales.

Morgan Gilot

© APMEP Juin 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

En début de Troisième, ma collègue et moi, lors de séances de co-enseignement, avons dû faire face à un constat sans appel: nos anciens élèves de Quatrième ne maîtrisaient pas les attendus de Quatrième sur le calcul littéral [1]. Nous avions pourtant le sentiment que cela avait été bien compris l’année précédente. Cependant, développer et réduire relevait de l’impossible pour quasiment tous nos élèves de Troisième. Nous avons alors pris conscience que nos manières d’aborder le point technique de la suppression des parenthèses dans une expression littérale étaient différentes, ce qui a posé souci lorsque les élèves ont été mélangés l’année suivante. Il est donc apparu comme absolument nécessaire de revoir notre copie sur notre manière de traiter cette notion. C’est pourquoi, dans mes classes de Quatrième, j’ai décidé de mener une expérimentation, basée sur la manipulation, qui permettait d’aborder le calcul littéral comme objet et non comme outil [2].

Pour avoir une chance de fonctionner, cette expérimentation devait reposer sur le triptyque manipulation – verbalisation – abstraction, tout en s’assurant que la manipulation ne soit pas un distracteur qui amènerait les élèves à ne retenir que « on a joué avec des jetons et des sacs » à l’issue des séances de travail.

Découvrir la distributivité simple

Cette première activité d’une heure se déroule entre septembre et octobre. Les élèves doivent manipuler des jetons pour faire émerger des propriétés et ainsi les généraliser.

L’idée est de faire manipuler les élèves sur des « nombres concrets » pour les amener ensuite à généraliser et à formaliser:

\(k \times (a+b)=k \times a+k \times b\).

Cette activité est réalisée en îlots, pour favoriser les échanges, les débats, les apports entre élèves (démarche socio-constructiviste). Les prérequis mathématiques nécessaires à cette activité sont le passage de la multiplication par un entier à l’addition itérée et les opérations sur les nombres relatifs (\(+\), \(-\), \(\times\)).

Extrait de l’activité 1¹.

Il est bon de rappeler que la distributivité en acte est travaillée dès le cycle 2, est approfondie au cycle 3 et commence à être vue de manière littérale en Cinquième [3]. Cette activité est donc un moyen de « raccrocher » tous les élèves et de formaliser une propriété normalement connue.

La manipulation

Dans cette étape de manipulation, l’élève utilise la distributivité, sans pour autant l’identifier forcément. Cette étape est primordiale car c’est elle qui servira de support à la schématisation qui permettra la verbalisation.

La schématisation et la verbalisation

À la suite des situations, l’élève doit schématiser une nouvelle situation:

(\(25\text{ ronds}+14\text{ rectangles})\times 2\)

L’objectif de cette étape est de faire émerger le concept de distributivité simple en assimilant le sac avec des parenthèses. Il écrit alors, dans « Calcul à effectuer »:

\(2\times25\text{ ronds}+2\times14\text{ rectangles}\).

C’est à ce moment que le \(+\) est introduit et vient remplacer le « et » que les élèves disent naturellement. Dans cette étape, le nombre de jetons de chaque type est trop grand pour permettre la manipulation. Cela contraint les élèves à l’abstraction.

Ensuite, l’élève complète:

• \(4\times(3\text{ ronds}+2\text{ rectangles})=\ …………………\) ;

• \(2\times(1,5\text{ rond}+6\text{ rectangles})= …………………\)

Dans ces exemples, le premier cas peut être traité à l’aide d’une manipulation, si certains élèves le souhaitent pour se rassurer. L’autre ne peut pas être réalisé concrètement et constitue un nouveau pas vers l’abstraction, une prise de distance avec la situation concrète de départ. Suite à cette étape, une synthèse écrite est demandée aux élèves: « Expliquez ce que vous avez compris dans ce que l’on vient de faire » (synthèse active). Les élèves ont alors écrit des propriétés comme « On multiplie chaque morceau du sac », appelant « morceau » les termes et « sac » les parenthèses. Cette formulation, bien que maladroite mathématiquement parlant, atteste néanmoins de la bonne compréhension du processus de calcul. Après une mise en commun, une synthèse passive est proposée, du type « Quand on multiplie (\(10\) ronds et \(4\) rectangles) par \(5\), on doit multiplier \(10\) ronds par \(5\) et on multiplie aussi \(4\) rectangles par \(5\):
\[\begin{aligned} (10 \text{ ronds} + 4 \text{ rectangles}) \times 5\\
= 10 \text{ ronds} \times 5 + 4 \text{ rectangles} \times 5\\
= 50 \text{ ronds} + 20 \text{ rectangles ».}\end{aligned}\]

Ce temps est essentiel. L’élève s’est interrogé, une mise en commun a été faite, puis validée par l’enseignant. Cette verbalisation se poursuivra, lors des étapes suivantes, quand les élèves échangeront dans leurs îlots et s’expliqueront mutuellement.

L’abstraction

On propose ensuite aux élèves de remplacer les jetons ronds par des « \(x\) » et les jetons rectangles par des « \(1\) ». Ainsi \(7\text{ ronds}+ 5\text{
rectangles}=7x+5\). On rappelle que les réductions \(7\times x=7x\) et \(x\times
x=x^2\) ont été vues en classe de Cinquième (sans pour autant être exigibles en évaluation), et lors de nombreuses questions flash [4] de début d’année de Quatrième (exercices de substitution). L’élève est alors invité à compléter les égalités suivantes (on n’exige pas d’étapes de calcul):

• \(2 \times (3x+5) = …………………\)

• \((5x+3) \times 4 = …………………\)

• \(5 \times (2x-6) = …………………\)

Les deux premiers cas sont réalisés sans grande difficulté car les élèves peuvent se ramener à la situation concrète: \(2\times(
3\text{ rectangles}+5\text{ ronds}) =6\text{ rectangles}+10\text{ ronds}=6x+10\). Cependant la troisième expression est bien plus complexe car elle ne peut pas être assimilée à la manipulation concrète introduite dans la première partie. Beaucoup d’élèves ont besoin de repasser par le schéma ci-dessous, même si cela n’a pas de sens concret. Cela leur permet d’aboutir à \(10x+(-30)\).

Cette dernière schématisation nécessite de bien maîtriser le fait que \(2x-6 =
2x + (-6)\). Il est ensuite proposé aux élèves de faire un autre exemple du même type: \((7x-11) \times 3\).

À ce stade, une synthèse est écrite, mettant en évidence les étapes de calcul:
\[\begin{aligned} 5 \times (2x-6) = 5 \times 2x + 5 \times (-6)\\
=10x+(-30)\\
=10x-30\end{aligned}\]
Cette activité, synthèses incluses, s’étend sur une heure de cours.

La consolidation

Lors de la séance qui suit cette activité, une feuille d’exercices est proposée. Dans cette dernière, dès le premier exercice, l’élève doit transformer des expressions données et découvre, pour la première fois les termes « forme développée » et « forme factorisée ».

Les élèves, même ceux qui rencontrent des difficultés, arrivent à effectuer ces transformations.

Supprimer des parenthèses

La deuxième activité², faite lors d’une autre séquence, au second trimestre, a pour objectif l’introduction de la réduction d’une expression littérale contenant des parenthèses. Le principe reste le même. On y retrouve la manipulation, la schématisation, la verbalisation, l’abstraction et la consolidation.

Pour effectuer \((49\text{ ronds}+10\text{ rectangles})-
(8\text{ ronds}+5\text{ rectangles})\), l’élève doit faire la schématisation ci-dessous pour arriver à verbaliser « On a \(49\) ronds et \(10\) rectangles. On doit enlever \(8\) ronds et \(5\) rectangles, ce qui revient à enlever \(8\) ronds et enlever \(5\) rectangles ».

Ensuite, après l’introduction de la l’abstraction, quand l’élève est face à \((7x+6)-(2x-5)\), il doit schématiser:

À l’aide de cette schématisation, il identifie « l’action à faire »: « J’ai \(7x+6\). Je dois enlever \(2x\) et enlever \(-5\) ». La verbalisation orale ici est essentielle.
\[\begin{aligned}(7x+6)-(2x-5)\\[-2pt]
=7x+6-2x-(-5)\\[-2pt]
= 7x+6-2x+5\\[-2pt]
= 5x+11\end{aligned}\]

Après cette série d’exercices de consolidation, une troisième activité³ de manipulation est également faite pour développer et réduire une expression littérale contenant des blocs de calcul intermédiaires.

Pour effectuer \(5\times (2\text{ ronds}+3\text{ rectangles}) – 2 \times(4\text{ ronds}+6\text{ rectangles})\), on schématise de la manière suivante:

La séquence s’est achevée sur des applications de la factorisation, du type « prouver que la somme de deux multiples de \(7\) est un multiple de \(7\) » ou encore « la somme de quatre entiers consécutifs est un multiple de \(2\) », afin d’arriver, en bout de séquence, à l’utilisation du calcul littéral comme un outil de preuve.

En février, les élèves de Quatrième ont été confrontés au premier devoir commun de l’année. L’énoncé de l’exercice portant sur le calcul littéral était:

On considère le programme de calcul (encadré) et l’expression \(A\) ci-dessous:

\[A = 7(2x-3)-(9x-28).\]

Démontrer que lorsque que l’on applique ce programme de calcul à \(x\), alors on obtient la même expression développée et réduite que l’expression développée et réduite de \(A\).

Lors de ce devoir, nous avons pu constater que les élèves n’en étaient pas tous au même stade d’avancement. En effet, il est apparu que certains avaient encore besoin de passer par la schématisation, quand d’autres étaient d’ores et déjà prêts à s’en passer.

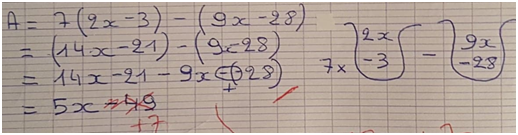
Conclusion

Josep Gascón [5] met en évidence que « dans le cas de l’algèbre élémentaire, comme dans beaucoup d’autres, le modèle implicite dominant dans l’enseignement secondaire correspond à ce que nous pourrions appeler la “conception du bon sens”. Sa caractéristique principale est l’identification de l’algèbre élémentaire à une arithmétique généralisée, modèle qui met l’accent sur le “symbolisme algébrique” et l’oppose à un supposé “langage arithmétique” que le premier est censé élargir et généraliser », ainsi que les limites de cette approche et met en avant la modélisation comme alternative.

Dans un enseignement par manipulation, le plus important est de garder en tête qu’une manipulation ne suffit pas et peut même s’avérer contre-productive.

En effet, si elle n’est pas associée à un enseignement clairement explicité, elle attirera l’attention de l’élève sur le contexte ludique de l’activité et pas sur le concept étudié. Cet écueil doit impérativement être évité.

Références

• [1] Éduscol. Attendus de fin d’année de Quatrième..Ministère de l’Éducation nationale.↩
• [2] R. Douady. « Jeux de cadres et dialectique outil-objet ».In : Recherches en didactique des mathématiques 7.n°2 (1986), pp. 5-31.↩
• [3] Éduscol. Repères annuels de progressions au cycle 4. . Ministère de l’Éducation nationale.↩
• [4] Éduscol. Documents d’accompagnement sur les types de tâches. . Ministère de l’Éducation nationale.↩
• [5] J. Gascón. « Un nouveau modèle de l’algèbre élémentaire comme  alternative à “l’arithmétique générali-sée” ». In :Petit x n°37 (1993), pp. 43-63.↩
• [6] S. Bissonnette et M. Richard. « Le cognitivisme et ses implications pédagogiques ». In :La pédagogie – Théorie et pratiques de l’Antiquité à nos jours. Sous la dir. de C. Gauthier et M. Tardif. 2^e éd. Montréal : Gaëtan Morin, 2005.
• [7] Centre Alain Savary. Dossier « Enseigner plus explicitement ». Dossier issu d’un groupe de travail, piloté par le bureau de l’éducation prioritaire de la DGESCO,visant à préciser et illustrer le concept d’explicitation tel qu’il est pensé dans le référentiel de l’éducation prioritaire. . Institut français de l’éducation.
• [8] Éduscol. Documents d’accompagnement sur le calcul littéral. . Ministère de l’Éducation nationale.
• [9] Éduscol. Programme de mathématiques du cycle 4. . Ministère de l’Éducation nationale.
• [10]C. Torossian et C. Villani.21 mesures pour l’enseignement des mathématiques. .Ministère de l’Éducation nationale, 2018.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Morgan Gilot est professeur de mathématiques au collège Pablo Neruda de Saint-Pierre-des-Corps (37).