Élèves plongés en plein cœur d’un monde virtuel
Depuis de nombreuses années déjà, on assiste au développement des mondes virtuels dans lesquels un joueur, représenté par son avatar, agit pour résoudre différents problèmes dans un environnement informatique. Dans ce contexte, les images à l’écran du monde virtuel et de l’avatar peuvent être utilisées dans un but d’apprentissage et d’enseignement. L’auteur propose ici de réfléchir à ce type d’utilisation auprès d’élèves de cycle 3, à partir du dispositif ANIPPO.
Richard Cabassut
© APMEP Mars 2022
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Le dispositif ANIPPO
ANIPPO (Application Numérique Interactive Pour des Problèmes Ouverts) [1] est un environnement virtuel 3D qui peut être implanté sur un ordinateur pour permettre la résolution de problèmes ouverts. L’élève dispose d’un avatar qu’il peut déplacer dans un environnement virtuel qu’il explore pour résoudre des problèmes auxquels il est confronté (Figure 1).

Figure 1 : Exemple d’avatar explorant un monde virtuel
Les caractéristiques de l’environnement, les instruments mis à la disposition de l’élève et les problèmes proposés sont variables. Dans le dispositif de recherche, un groupe de quatre à six élèves est extrait de la classe pour aller travailler dans une salle. Chaque élève travaille individuellement avec un ordinateur. Grâce au casque et au micro mis à sa disposition, il peut collaborer avec les autres élèves extraits de la classe, chacun identifié par un avatar différent apparaissant à l’écran.
La variation des énoncés de problèmes proposés
L’idée des concepteurs1 a été de proposer des problèmes se situant dans l’espace tridimensionnel permettant de mobiliser le vocabulaire et la vision de la géométrie de l’espace. Plus particulièrement, il était proposé d’étudier un solide constitué d’un grand cube (construit par assemblage de petits cubes élémentaires) auquel une partie a été retirée. L’illustration suivante (Figure 2), propose un exemple avec un cube 3 x 3 x 3 dans lequel un tunnel central a été retiré.
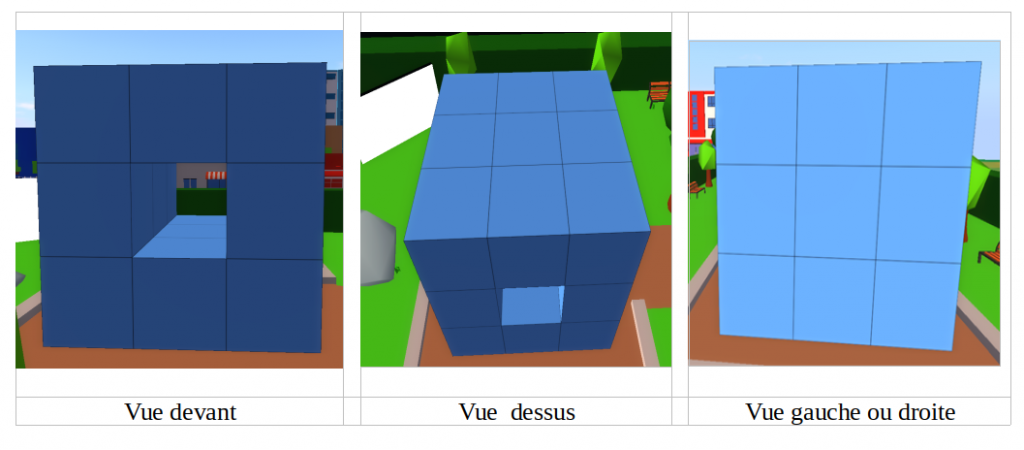
Figure 2 : Différents points de vue d’un exemple de solide
Énoncé d’un problème de volume d’un solide :
|
Combien de petits cubes bleus faut-il pour former le solide (formé par un grand cube auquel on a enlevé des petits cubes) ? |
Énoncé d’un problème d’aire d’un solide :
|
Chaque petit cube a des faces carrées. Combien de faces carrées faut-il pour couvrir le solide (y compris dans la partie intérieure où on a enlevé des petits cubes) ? |
Énoncé d’un problème de patron d’un solide :
|
Le solide formé par les petits cubes est constitué d’un grand cube auquel on a enlevé des petits cubes à l’intérieur. On cherche à remplir ce trou avec un solide de manière à reconstituer un cube plein. Construire un patron de ce solide. |
Ce dernier problème a vite été abandonné en raison des difficultés déjà rencontrées dans les problèmes de dénombrement.
La différenciation s’est appuyée sur deux variables :
-
la taille du grand cube évidé ;
-
la complexité de la partie évidée (Figure 3).

Figure 3 : Variation de la taille et de la cavité
Quelques caractéristiques du dispositif
Collaboration
La situation de résolution de problèmes est collaborative à partir du moment où « des personnes de même niveau cognitif, dont les statuts sont équivalents, sont capables de travailler ensemble dans un but commun ». Cette situation est ensuite considérée comme « interactive » si ces personnes communiquent de façon « soutenue, argumentent, voire s’opposent en évitant toutefois d’imposer leurs points de vue » [2, p.116]. Or, dans l’environnement ANIPPO, les élèves ont la possibilité de communiquer entre eux par le biais de leur casque/micro ou par écrit grâce à leurs avatars qui circulent dans l’espace virtuel …
On observe des élèves qui réalisent les tâches sans collaborer alors que d’autres collaborent entre eux, soit pour mieux s’approprier l’environnement (« Comment tu fais pour … ? » ), soit pour connaître la réponse à un problème, mais pas pour savoir comment cette réponse a été trouvée, ni pour la remettre en cause.
Les registres de représentation de ANIPPO
Les résultats de la recherche [3] montrent l’importance des représentations dans l’enseignement et l’apprentissage des mathématiques. L’environnement ANIPPO permettra de travailler avec différents registres de représentation [4].
Le registre du monde virtuel ANIPPO
Dans ce registre, différents traitements sont possibles :
-
le déplacement d’un avatar dans l’environnement par des commandes au clavier, ou à la souris ;
-
le contrôle visuel à l’écran d’un déplacement virtuel d’un avatar,
-
l’exploration visuelle à l’écran d’un lieu virtuel. Ici c’est un réel avantage puisque dans une situation de manipulation réelle, si le cube évidé est trop petit par rapport au manipulateur, ce dernier ne pourra pas entrer dedans pour observer sa cavité intérieure.

Figure 4 : Exploration de la cavité du cube
Les registres écrit, graphique ou oral
Dans les discussions (chats) entre élèves, ils peuvent échanger des informations écrites sur la recherche de lieux ou de procédures. Pour y accéder ainsi que pour se déplacer, demander de l’aide, voir l’énoncé du problème ou réaliser d’autres actions, l’élève doit se servir d’une barre de tâches où les informations sont exprimées par un texte écrit ou un graphique légendé.
Concernant les problèmes, l’élève doit produire à l’aide du clavier différents textes écrits : une réponse à la question posée puis une explication de cette réponse.
À l’oral, différents échanges peuvent avoir lieu (toujours à l’aide du casque et du micro) :
Dans le cas des dispositifs mis en place, il est difficile de déterminer si certains registres et certains passages d’un registre à l’autre sont favorisés ou non par l’environnement virtuel par rapport à un environnement traditionnel.
Il est clair cependant que des traitements inter-registres ou intra-registres peuvent aboutir à une reformulation incorrecte de l’énoncé.
-
avec l’avatar qui conseille et aide l’élève,
-
avec les avatars des autres élèves, pour enregistrer l’explication orale demandée par l’environnement,
-
lors de l’entretien d’explicitation, en ligne, avec un chercheur.
En effet chaque élève doit répondre au problème pour lequel un automate demande dans un premier temps une explication à écrire dans une fenêtre, et dans un second temps une explication orale (enregistrée au micro). La demande d’explication sera renouvelée lors de l’entretien d’explicitation qui suit immédiatement chaque séance. Cet entretien se fait à distance avec un chercheur de l’un des trois laboratoires du projet.
Duval [4, p.126] distingue les traitements intra-registres (comme le déplacement à l’intérieur de l’environnement ANIPPO, ou encore le dénombrement de petits cubes par un calcul sur des nombres écrits en chiffres) et les traitements de conversion inter-registres (comme la description orale, à l’avatar d’un camarade, en langage naturel, d’un déplacement dans l’environnement ANIPPO, ou le repérage en langage naturel d’un objet situé dans l’espace virtuel ANIPPO, ou encore l’explication orale ou écrite d’une procédure en actes).
On observe que :
-
le registre de l’action semble dominer dans l’appropriation et la résolution de problèmes ;
-
le registre oral est abondant entre pairs (mais pas systématique, certains élèves travaillant de manière isolée) dans l’appropriation et moins présent de manière surprenante, dans les phases de résolution de problèmes. Peu d’élèves expliquent oralement comment ils ont trouvé la réponse (alors qu’il leur est explicitement demandé une explication orale au micro). De même, peu d’élèves échangent oralement au micro sur les démarches et procédures pour résoudre les problèmes. La culture de la justification d’une action ou d’une procédure, ou du retour réflexif sur celles-ci n’est pas encore installée.
Le registre de l’écrit est utilisé de manière très marginale. L’utilisation de la discussion écrite, y compris entre pairs est peu fréquente, car ils préfèrent les échanges oraux.
Changer de registres
D’une part on observe des difficultés à décrire ou expliquer par écrit ce que l’élève a fait. D’autre part, on observe également parfois des variations d’explications entre l’explication écrite fournie lors de la résolution et l’explication orale au micro ou lors de l’entretien suivant la résolution. Ceci semblerait montrer que l’explication d’une réponse varie en fonction du registre d’explication (action, écrit, oral) ou du récepteur de l’explication (groupe d’élèves, élève seul, chercheur, fenêtre anonyme…).
Dans le cas des dispositifs mis en place, il est difficile de déterminer si certains registres et certains passages d’un registre à l’autre sont favorisés ou non par l’environnement virtuel par rapport à un environnement traditionnel.
Il est clair cependant que des traitements inter-registres ou intra-registres peuvent aboutir à une reformulation incorrecte de l’énoncé.
En voici un exemple
|
Combien de petits cubes bleus faut-il pour former le solide (formé par un grand cube auquel on a enlevé des petits cubes) ? |
|
Jean répond : il faut 5 petits cubes. Es-tu d’accord ? Explique pourquoi. Un élève répond qu’il n’est pas d’accord et explique que la réponse correcte est 8. En effet il faut 8 petits cubes pour construire le grand cube auquel on enlèvera ensuite 2 petits cubes pour former le solide de la figure. L’élève a compris la situation ; il répond correctement à la question qui n’a pas été posée : « Combien le grand cube initial a-t-il de petits cubes ? » Il semblerait que certains élèves aient des problèmes de mémorisation de la question énoncée. Les souvenirs qu’ils en ont les amènent à reconstituer cet énoncé en un nouvel énoncé auquel ils vont répondre et non équivalent à l’énoncé initial. |
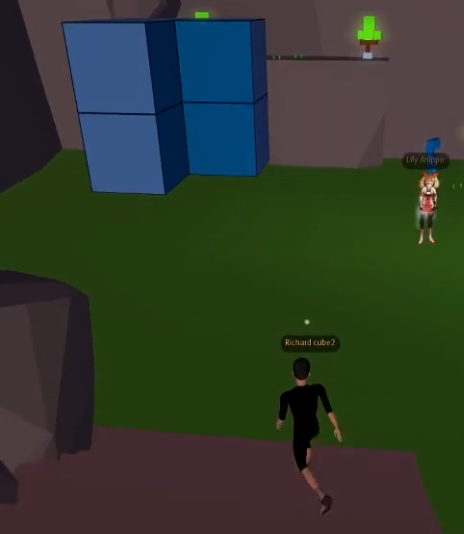 Figure 5 |
Facteurs à prendre en compte
L’environnement instrumental
Le fonctionnement de ANIPPO sur les ordinateurs a été problématique en raison de nombreux incidents. Par exemple, la connexion Internet ayant de nombreuses défaillances n’a pu permettre d’assurer l’enregistrement vidéo et audio des actions à l’écran ou des entretiens à distance ou en local entre élèves et chercheurs : « Les problèmes techniques de
-
lire les panneaux d’information ;
-
à voler alors qu’ils savent voler ;
-
à échanger des informations avec des camarades ;
alors que d’autres savent exploiter les ressources des différents instruments. Par exemple, des élèves pensent à utiliser le vol pour explorer l’intérieur du cube, pour compter ce qui est en moins, ou pour sauter dans le labyrinthe pour voir, au dessus des couloirs du labyrinthe, où est la sortie.
Le temps d’appropriation
Alors qu’au début de l’expérimentation, seul un début de séance était consacrée à l’appropriation de l’environnement, une séance toute entière lui était dédiée dans le dernier dispositif mis en place car ce temps d’appropriation avait clairement été sous-estimé. Cela n’est pas sans rappeler le manque de temps dont se plaignent souvent les enseignants.
Thèmes mathématiques
Il semblerait que la géométrie dans l’espace, pourtant au programme du cycle 2, soit mal maîtrisée par des élèves de cours moyen ; par exemple, certains élèves s’expriment en confondant cube et carré.
Les procédures utilisées2 et leurs justifications
Du côté des pratiques, beaucoup de procédures sont en actes (naturelles) et les élèves ont des difficultés à les justifier. Par exemple, dans le micro-espace réel tourner un petit cube évidé qui tient dans la main est une technique en acte assez naturelle qu’on ne sait pas justifier et qui permet d’observer. Par contre dans le méso-espace tourner, à pied, autour d’un très gros cube évidé, pour l’observer, est coûteux en terme de durée et l’action n’est pas naturelle. Pour réaliser ce déplacement il faut avoir l’intention d’explorer en faisant faire, à son avatar, le tour du cube. Cette intention d’exploration est une justification de ce déplacement. On observe bien souvent des déplacements aléatoires dans certaines directions, sans qu’on devine une intention qui a anticipée ce déplacement.
Face aux procédures de dénombrement (et donc pas seulement de comptage mais également celles utilisant des calculs), les élèves ont souvent des fragilités liées à la non-acquisition de la compétence d’énumération (les élèves oublient de compter des cubes ou en comptent en double car ils ne savent pas énumérer).

Figure 6 : Combien de petits cubes pour ce solide ?
Par exemple, pour dénombrer les petits cubes du solide de la Figure 6, un élève répond 28 et fournit à l’avatar la réponse suivante « C’est 28 je crois parce 4 fois 7 ça fait 28 » et plus loin pour expliquer « Ben j’ai compté tous les cubes. Au début j’ai compté ceux du bas. Comme il y a 3 d’un côté et 4 de l’autre, 3 fois 4 ça fait 12. Et après quand j’ai rajouté tous les autres cubes ça fait 28 ». Lors de l’entretien avec le chercheur il explique : « La première fois j’ai compté combien y avait de cubes. Je suis tombé sur plusieurs résultats. Et après j’ai décidé de faire techniquement : de compter tout ce qu’il y avait en bas, tout ce qu’il y avait en haut et j’ai compté le reste. Je suis tombé sur 28. Et donc c’était juste ».
Un autre élève justifie 54 petits cubes par l’explication : « 9 cubes par faces et 6 faces ».
Bien entendu on trouve aussi des procédures correctes. Par exemple, un élève répond 24 et justifie : « J’ai calculé d’abord les cubes du bas puis j’ai fait fois deux car en haut c’est la même chose. Et après j’ai compté les cubes qui restaient au milieu », ce qui correspond au calcul 2 x 9 + 6.
Du côté des justifications des pratiques, les élèves semblent confondre « décrire ce que j’ai fait » et « expliquer ou justifier ce qui est fait ». Dans l’exemple précédent l’élève décrit que 28 = 7 x 4 mais n’explique pas d’où vient le 7 et le 4 dans le calcul. En fait il a obtenu 28 par comptage et quand on lui demande d’expliquer comment il l’a obtenu, il précise une propriété arithmétique de 28, en proposant une décomposition multiplicative, mais ceci n’est pas une explication de sa procédure. Cet élève comprend-il la consigne « explique ton résultat » ou reformule-t-il cette consigne en « donne des propriétés du résultat que tu as trouvé » ? En d’autres termes une partie des problèmes de certains élèves ne seraient pas d’ordre mathématique mais de l’ordre sémantique : la compréhension de la consigne qui est reformulée incorrectement en une autre consigne.
Les travaux de ERMEL de l’INRP [6] ont montré l’importance, dès l’école primaire, du raisonnement de justification. On observe dans cette expérience, chez de nombreux élèves, l’absence de justification, des justifications irrationnelles (on ne comprend pas l’inférence entre la raison avancée et la technique utilisée), par contrat habituel (j’ai additionné parce que d’habitude on fait une addition), par modélisation (correcte ou non).
Espace virtuel et apprentissage : attention aux mythes !
Les visions de l’apprentissage et de l’enseignement reposent souvent sur des mythes de dispositifs magiques qui conduisent à la réussite des élèves. Par exemple, K. J. Carbonneau, S. C. Marley et J. P. Selig [7] mettent en garde contre le mythe de la manipulation. F. Amadieu et A. Tricot questionnent le mythe du numérique [8]. Nous avons dans cet article proposé une réflexion sur l’utilisation des espaces virtuels comme contexte d’apprentissage et d’enseignement. Dans ces espaces, la manipulation est virtuelle et le numérique joue un rôle primordial. Il serait naïf de croire que les espaces virtuels facilitent l’apprentissage. Dans l’exemple ANIPPO, on voit que les difficultés liées aux différents registres de représentations sont nombreuses, dans les traitements intra-registres et dans les conversions inter-registres. Un des intérêts dans l’apprentissage des situations proposées est de développer, chez l’élève, différentes compétences : chercher, raisonner, représenter, modéliser, communiquer. Après les premiers questionnements sur les avantages et les inconvénients de ces mondes virtuels, il faudra donc réfléchir à différents scénarios didactiques et pédagogiques intégrant ces mondes virtuels.

Références
-
[1] Pacurar, E., Magot, C.-A., Cabassut, R., Solon, Y. (2020) Virtual manipulatives in inquiry based approach of 3D open problems by French 5th graders. Teaching Mathematic and Computer science. DOI: 10.5485/TMCS.2020.0507 Téléchargeable sur :
 ↩
↩ -
[2] Baudrit, A. (2007) Apprentissage coopératif/ Apprentissage collaboratif : d’un comparatisme conventionnel à un comparatisme critique. Revue Les sciences de l’Education – Pour l’Ère nouvelle. 2007/1 Vol.40, p. 115 à 136↩
-
[3] Goldin, G. A. (1998). Representational systems, learning, and problem solving in mathematics. The Journal of Mathematical Behavior, 17(2), 137–165.↩
-
[4] Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics 61, 103–130↩
-
[5] Trestini, M., Cabassut, R. (2006). La domination de la technique sur l’action didactique et sur les scénarios pédagogiques en formation à distance. Colloque international TICE 2006. INP de Toulouse.
-
[6] Douaire, J., Emprin, F., Rajain, C. (2009). L’apprentissage du 3D à l’école, des situations d’apprentissage à la formation des enseignants, Repère n° 76, Topic éditions.↩
-
[7] Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105, 380-400↩
-
[8] Amadieu, F., Tricot, A. (2014). Apprendre avec le numérique. Mythes et réalités. Édition Retz.↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Richard Cabassut est retraité de l’enseignement supérieur depuis 2021 mais termine ses projets de recherche, parmi lesquels ANIPPO.
Il fait partie du comité de rédaction d’Au Fil Des Maths.
-
Ce projet se développe dans le cadre de l’agence nationale de la recherche (https://anr.fr/Projet-ANR-18-CE28-0002) et réunit des chercheurs de différents laboratoires (CIREL Université de Lille, ADEF Université d’Aix-Marseille, LISEC Université de Strasbourg)↩
-
Les procédures utilisées sont observables dans les vidéos d’écran ou les réponses et explications écrites.↩

Une réflexion sur « Élèves plongés en plein cœur d’un monde virtuel »
Les commentaires sont fermés.