Quadrature
Créée en 2012, l’association Résonance – Art & Science se propose de mêler les arts du vivant et les sciences. La première de la conférence dansée Quadrature s’est tenue à l’occasion des SurpreNantes Journées Nationales de l’APMEP, le 21 octobre 2017. François Sauvageot présente ici l’élaboration de cette conférence singulière.
François Sauvageot
© APMEP Juin 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Quadrature
Cette conférence dansée est issue d’un long processus de maturation commencé en 2015, prenant appui sur des activités développées lors de la Fête de la Science et du salon de la culture et des jeux mathématiques depuis 2004.
Au cours de cette histoire, on trouve trois éléments en apparence hétéroclites : une pièce de Samuel Beckett [1], un jeu de baguenodier et des codes informatiques. La première date de 1980 et a été écrite pour la télévision. Du second, on trouve trace dans un ouvrage d’un moine franciscain Luca Pacioli , ami de Leonardo Da Vinci , à qui il enseigne les maths et qui en retour illustre ses livres de géométrie. Le rêve de tout enseignant ! Le manuscrit n’a été publié qu’en 1997 mais a été écrit entre 1496 et 1508. C’est Édouard LUCAS qui popularise le jeu en France dans ses Récréations mathématiques [4] (et lui donne la graphie liée à l’étymologie nœud de bagues que lui revendique un certain clerc de notaire lyonnais) datant de 1882 et disponibles en ligne. Enfin les derniers remontent à l’utilisation du binaire au XVIe siècle, même si on peut aussi les associer au papyrus de Rhind (Égypte, \(-1500\)) ou au Yi Jing (Chine, \(-750\)).
Représentations géométriques
Le lien entre ces trois éléments est le cube, ou plutôt l’hypercube, que l’on peut obtenir à partir de segments ou tout simplement de \(0\) et de \(1\). Un segment est une ligne joignant deux sommets, notés \(0\) et \(1\). C’est un objet ayant une seule dimension ou plutôt formé de deux objets de dimension nulle, les sommets, et d’un objet de dimension un. Un carré est un produit (cartésien) de deux segments.
Figure 1. Un carré vu comme produit cartésien de deux segments – Sommets notés en binaire.
Un carré se représente avec quatre sommets que l’on peut numéroter \(00\), \(01\), \(10\) et \(11\) comme on écrit des nombres à deux chiffres en binaire. Les segments joignent alors les nombres qui ne diffèrent que d’un seul chiffre, et la position du chiffre qui diffère donne la direction du segment qui les joint : \(00\) et \(10\) sont joints par une arête verticale tandis que \(10\) et \(11\) sont joints par une arête horizontale. En revanche, \(00\) et \(11\) diffèrent de deux chiffres et ne sont pas reliés par une arête.
On peut généraliser en itérant cette procédure de produit. L’algèbre est en ce regard plus commode que la géométrie. Un mot codé est un mot formé de \(0\) et de \(1\). Comme dans l’exemple précédent, il est utile de conserver les \(0\) initiaux, mais à ce détail près, un mot peut s’interpréter comme un nombre écrit en binaire : \(0100110\) est un mot de longueur \(7\), que l’on peut interpréter comme \(0\times2^6+1\times2^5+0\times2^4+0\times2^3+1\times2^2+1\times2^1+0\times2^0\), i.e. \(38\). Comme on le voit il y a donc \(2^n\) mots de longueur \(n\), correspondant aux nombres de \(0\) à \(2^n-1\) écrits en binaire. Un mot a des voisins : ce sont les mots qui diffèrent de lui en une et une seule position. Par exemple \(38\) et \(34\) sont voisins, ils ne diffèrent que par le chiffre correspondant à \(2^2\) : \(0100110\) et \(0100010\).
Correction d’erreurs
La terminologie s’explique quand on a une vision géométrique du code, mais la notion de voisinage peut aussi intervenir quand on songe à des questions de transmission. C’est par exemple là que rentrent en jeu les codes correcteurs d’erreur. L’encodage consiste à transformer des symboles (lettres, chiffres, etc.) en mots binaires, par exemple le code ASCII d’un caractère ou encore le code Baudot, du nom d’Émile Baudot qui obtint une médaille d’or à l’exposition universelle 1878 pour son invention. C’est d’ailleurs de son nom qu’est dérivée l’unité de transmission : le baud (Bd).

Figure 2. Émile Baudot et son code.
Si donc, durant une transmission, une erreur se produit, le signal est bruité, et un des chiffres vient à être incorrect, alors le mot reçu est un voisin du mot envoyé. En un sens le mot reçu est presque celui envoyé. La distance qui permet de quantifier ce « presque» est la distance introduite par Richard HAMMING dans un article de 1950 : la distance entre deux mots est simplement le nombre de chiffres par lesquels ils diffèrent. C’est ainsi qu’en adjoignant un bit de parité, à savoir un \(0\) ou un \(1\) selon que le mot contient un nombre pair ou impair de \(1\), on peut détecter s’il y a eu une erreur de transmission. Par exemple si \(38\) est émis, soit \(0100110\), et donc avec le bit de parité : \(10100110\), et que l’on reçoit \(10100010\), à savoir \(34\) avec un bit de parité égal à \(1\), on sait qu’il y a eu une erreur car le bit de parité correct pour \(34\) est \(0\). En fait le bit de parité fait en sorte qu’en tout il y ait un nombre pair de \(1\), ce qui n’est pas le cas avec \(10100010\).
Toutefois cette technique ne permet pas de rectifier l’erreur. En effet \(10100010\) a de nombreux voisins qui auraient pu produire l’erreur. Par exemple \(42\) ou \(38\), mais en fait n’importe lequel des huit nombres obtenus en modifiant un chiffre est acceptable ! C’est pour cette raison que Richard HAMMING a introduit le code de Hamming. Dans ce dernier, la distance minimale entre deux mots transmis est de \(3\) et donc tous les voisins d’un mot correct ont en fait un seul tel voisin et il est donc possible de réparer l’erreur (à condition qu’il n’y en ait qu’une). On peut mettre en scène ce code en demandant à une personne du public de répondre à des questions en ayant le droit de mentir au plus une fois et d’une part en trouvant la réponse correcte et d’autre part en indiquant si la personne a menti et quand. C’est impressionnant, mais quand on y réfléchit, pas plus que le fait qu’un téléphone portable fasse cela en permanence sans qu’on ne s’en rende compte !
Les mots en binaire permettent de modéliser de nombreuses situations, le \(0\) symbolisant l’absence et le \(1\) la présence.

Figure 3. Un baguenodier.
Par exemple dans le baguenodier, le chiffre \(1\) symbolise le fait que l’anneau situé à la même position que le chiffre est prisonnier de la tige métallique. Le jeu est d’autant plus amusant qu’il prend la forme d’un casse-tête. Physiquement on ne peut changer de position qu’un seul anneau à la fois : soit le plus à droite (qui correspond au chiffre des unités), soit celui immédiatement à gauche de l’anneau prisonnier le plus à droite. Par exemple on peut passer de \(38\) à \(34\) et réciproquement car ils diffèrent du chiffre des puissances \(2\) et leur chiffre \(1\) le plus à droite est celui des puissances \(1\) : \(0100\underline{1}\mathbf{1}0\) où est en gras le chiffre \(1\) le plus à droite et est souligné celui que l’on peut modifier pour passer de \(38\) à \(34\). Le jeu consiste à libérer tous les anneaux, donc à obtenir \(0\), à partir d’une position où ils sont tous prisonniers, donc en partant de \(127\). On le fait en passant de voisin à voisin quand c’est possible.
La fin du parcours peut par exemple ressembler à ceci : \[0000111\to0000110\to0000010\to0000011\to0000001\to0000000\] Les chemins sont assez simples à explorer. En effet, à chaque étape, on a au plus deux possibilités. Soit changer le chiffre des unités, soit le chiffre précédant le \(1\) le plus à droite (quand il existe). Puisque chaque position a exactement deux voisines atteignables à l’exception de \(1000000\) et \(0000000\), on en déduit que l’ensemble des positions est tout simplement un chemin qui va d’étape en étape depuis \(1000000\) jusqu’à \(0000000\) de façon univoque ! En particulier \(1111111\) a deux voisins, l’un amène dans la mauvaise direction, i.e. vers \(1000000\), et l’autre dans la bonne. Il se trouve que la bonne direction est celle qui est contre-intuitive, et en plus le chemin est plus long que dans l’autre sens ! Il faut \(85\) étapes pour arriver au bout, et donc \(42\) pour arriver au bout de la fausse piste.
C’est à partir de ce jeu que nous avons créé en 2004 une animation pour la fête de la science, proposée par la suite au salon du CIJM (Comité International des Jeux Mathématiques), avec comme objectif d’introduire la numération binaire.
Il existe une représentation visuelle de la solution, avec trois anneaux. Voici les positions et les chemins possibles.
Figure 4. Un code de Gray & Frank Gray.
Ce chemin qui joint tous les mots du code (les mots sont de longueur \(3\) sur le dessin, mais c’est général) a donc la particularité de ne changer qu’un seul des chiffres à chaque étape. On a ainsi tous les nombres de \(0\) à \(7\) en suivant la suite \(0-1-3-2-6-7-5-4\). Il est remarquable que le dernier nombre ne diffère lui aussi du point de départ que d’un chiffre. Ces objets ont intéressé de nombreuses personnes. On parle de chemin hamiltonien ou de cycle hamiltonien pour désigner les chemins sur l’hypercube qui passent par tous les sommets une fois et une seule, éventuellement en réalisant une grande boucle dans le cas des cycles. Si ces chemins hamiltoniens ont la propriété de proximité, i.e. chaque voisin sur le chemin est aussi voisin au sens de , alors on parle de code de Gray ou de code de Gray cyclique. Sir William Rowan HAMILTON est un mathématicien et physicien irlandais bien connu pour ses contributions à la mécanique, à l’algèbre linéaire et bien entendu pour son invention des quaternions. Frank GRAY est un ingénieur et physicien américain, impliqué dans le développement de la télévision et connu pour avoir déposé un brevet sur un code ayant la propriété de proximité. Ces derniers sont utilisés lors du codage des adresses à l’intérieur des disques durs (physiques) : moins on change de chiffres, plus on peut faire bouger la tête de lecteur rapidement et plus la lecture est fiable.
| (a) Code binaire usuel. | (b) Code de Gray. |
Figure 5. Codeurs rotatifs.
En 2004 l’histoire s’arrête là et la partie « physique », i.e. manipulatoire, de l’animation consiste à se débattre avec le baguenodier. C’est amusant pour ce public averti, mais l’association Résonance cherche à présenter des activités où la partie corporelle est plus développée. Nous voulons en effet nous adresser à des jeunes en partant de danse contemporaine et les amener aux maths. Nous visons par ailleurs un public d’adultes pour qui les maths restent trop souvent un souvenir douloureux assorti d’une frustration née d’un amour déçu. Et c’est ici que Samuel entre en jeu !
Quad
Écrit en 1980 pour la télévision, Quad fut mis en scène et réalisé en 1981 par Samuel Beckett et diffusé en R.F.A. le 8 octobre 1981 sous le titre Quad I & II, puis diffusé sur BBC 2 en Grande-Bretagne le 16 décembre 1982. Gilles Deleuze en a tiré un commentaire savant sous le titre L’épuisé, paru aux Éditions de Minuit en 1992. Nous nous sommes plus particulièrement intéressé\(\cdot\)e\(\cdot\)s aux contraintes chorégraphiques que s’est imposé Beckett, sans parvenir à les satisfaire. Ces contraintes peuvent s’interpréter très simplement grâce aux hypercubes et aux codes de Gray. Le nom de codes de Gray-Beckett en a même été tiré. Contrairement aux codes de Gray généraux, les codes de Gray-Beckett n’ont pas encore d’utilité reconnue car ils sont encore très mal compris. Ce qui est toutefois remarquable c’est qu’on connaît tous les codes pour \(n\) inférieur à \(6\), qu’on en connaît jusqu’à \(n=8\)… et que les résultats actuels s’arrêtent là !
Voici les contraintes qu’impose la pièce, pour quatre danseur\(\cdot\)se\(\cdot\)s :
-
chaque configuration (les quatre solos, les six duos, les quatre trios et le quatuor) doit apparaître sur scène une et une seule fois ;
-
entre chaque tableau une personne exactement fait son entrée ou sa sortie ;
-
en cas de sortie du plateau, c’est la personne présente sur scène depuis le plus longtemps qui doit sortir ;
-
au contraire, si c’est une entrée, il n’y a pas de contrainte supplémentaire ;
-
au début la scène est vide et à la fin aussi.
Voici comment interpréter ces consignes avec un hypercube :
-
chaque tableau est symbolisé par un mot binaire de longueur \(4\), i.e. un sommet de l’hypercube de dimension \(4\) : par exemple \(0100\) indique un solo du deuxième danseur et \(1001\) un duo des première et quatrième danseuses ;
-
tous les sommets du cube doivent être visités une fois et une seule lors de la chorégraphie ;
-
chaque changement de tableau correspond à un déplacement le long d’une arête de l’hypercube (i.e. on passe d’un sommet à un sommet voisin) et donc, avec la contrainte précédente, ceci signifie que la chorégraphie est représentée par un chemin hamiltonien sur l’hypercube ;
-
si on change un \(0\) en \(1\), on peut le faire sur n’importe quel \(0\) ;
-
si on change un \(1\) en \(0\), on doit le faire sur le \(1\) correspondant à la personne présente sur scène depuis le plus longtemps, ce qui ne s’interprète pas facilement sur le cube ;
-
on veut en fait un cycle hamiltonien démarrant par le mot \(0000\).
Après avoir longtemps cherché, Samuel Beckett a jeté l’éponge et s’est résigné à ne pas obéir à toutes ces contraintes. En fait sa chorégraphie est par trop symétrique et, de ce fait, s’autorise à répéter certaines configurations. Ce n’est pas vraiment de sa faute, puisqu’il n’existe aucun code de Gray-Beckett pour \(n=4\) ! Afin de s’en convaincre, voici une petite analyse visuelle du problème que nous avons développée pour nos activités lors de la fête de la science ou pour des animations ponctuelles. Étudions successivement les dimensions \(2\) et \(3\).
Chorégraphie pour deux danseur\(\cdot\)se\(\cdot\)s
Tout d’abord la quadrature du carré version Beckett ! Une couleur (jaune ou cyan) et une position dans le mot (chiffre de droite ou chiffre de gauche) sont associées à chaque danseur\(\cdot\)se et on traduit les contraintes précédentes mais pour deux personnes. La figure associée est un carré, numéroté \(00\), \(01\), \(11\), \(10\) ou encore : noir (vide), jaune, jaune et cyan, cyan. Le parcours sur le carré sera noté par des flèches. Voici les indications chorégraphiques :
Figure 6.
La scène est vide, puis se remplit avec le danseur jaune. On passe de \(00\) à \(01\) et on note ce mouvement sur le carré par une flèche. Ainsi on sait qui doit sortir juste en regardant le cube. Ici ce serait le danseur jaune, ce qui est impossible car la scène ne peut se vider qu’à la fin du spectacle.
Figure 7.
Le danseur jaune est donc rejoint par la danseuse cyan et on en garde le parcours en mémoire. On voit sur le cube qu’il y a deux flèches vers la droite ou le haut, donc deux personnes qui sont entrées et ne sont pas encore ressorties. De plus le jaune précède le cyan dans le parcours, donc si quelqu’un doit sortir c’est le danseur jaune. On voit aussi qu’on est en \(11\) (avec donc deux couleurs visibles).
Figure 8.
Comme personne ne peut rentrer car le duo est au complet, on fait sortir le danseur jaune. Les deux flèches horizontales sont passées en pointillées : le danseur jaune est entré (flèche vers la droite) puis sorti (flèche vers la gauche). On est en \(10\) et seule la danseuse cyan est en scène.
Figure 9.
On ne peut pas faire rentrer le danseur jaune car on reverrait alors le duo. On ne peut donc que faire sortir la danseuse cyan. Ce qui tombe bien car cela permet d’accomplir la dernière étape de la chorégraphie tout en respectant les consignes : revenir au point de départ (scène vide) en passant par tous les points (deux solos et un duo) possibles, en n’empruntant que des arêtes (une entrée ou une sortie à la fois) du carré, avec un déplacement inverse correspondant au déplacement direct le plus ancien (sort la personne qui est sur scène depuis le plus longtemps). On constate également qu’à part la première personne à rentrer, aucune alternative ne s’est présentée. On en déduit qu’il y a deux codes de Gray-Beckett (cycliques) pour \(n=2\), à savoir : \(00-01-11-10-00\) et 0\(0-10-11-01-00\). Ils sont inverses l’un de l’autre.
En fait, c’est un sacré hasard. Il n’y a en effet aucune raison pour qu’un code de Gray-Beckett soit réversible, à cause de la non-symétrie des consignes quant aux entrées et aux sorties.
Chorégraphie pour trois danseur\(\cdot\)se\(\cdot\)s
On s’intéresse maintenant la dimension \(3\) : trois danseur\(\cdot\)se\(\cdot\)s et donc aussi trois couleurs). On va voir qu’il n’y a pas de code Gray-Beckett pour \(n=3\) ! On se munit donc d’un cube et de trois couleurs.
Pour le premier essai, on fait entrer les trois couleurs successivement (jaune, cyan, bleu). On ne peut alors que faire sortir successivement jaune puis cyan. Comme il reste encore un duo à voir, bleu ne peut pas sortir et on fait entrer jaune. On se retrouve alors dans une impasse : deux personnes sont sur scène, mais on a déjà vu le trio ainsi que les solos des danseur\(\cdot\)se\(\cdot\)sjaune et bleu. En fait seul manque le solo de la personne qui n’est pas sur scène, et il faudrait donc faire sortir deux personnes et en faire rentrer une ! Bref, la tentative se solde par un échec.
| (a) Essai 1. | (b) Essai 2. | (c) Essai 3. |
Figure 10. Exploration du cas \(n = 3\).↩
On effectue un nouvel essai ! Puisqu’on sait qu’il ne faut pas faire rentrer les trois danseur\(\cdot\)se\(\cdot\)s successivement et qu’on ne peut pas faire ressortir la première juste après son entrée, on en fait rentrer deux, puis ressortir la première. Comme on ne peut alors ni faire sortir le second, ni faire re-rentrer la première, on doit alors faire entrer la dernière. On a alors deux choix. Soit faire entrer à nouveau la première danseuse (essai 2 (figure 10b)), soit faire sortir le second (essai 3 (figure 10c). L’essai 2 se solde par un échec car il faudrait in fine faire sortir la première danseuse, mais c’est au dernier de sortir ! Quant à l’essai 3, c’est sans doute la meilleure des trois tentatives. On a trouvé un code de Gray-Beckett, mais il n’est pas cyclique. Le trio assure le final et la scène se vide d’un coup, ce qui ne convient pas. Voici toutefois le code : \(000-001-011-010-110-100-101-111\).
Chorégraphie pour quatre danseur\(\cdot\)se\(\cdot\)s
Pour expérimenter avec quatre danseur\(\cdot\)se\(\cdot\)s il faudrait avoir une représentation visuelle. C’est ici qu’intervient Alicia Boole (1860-1940), mathématicienne irlandaise autodidacte, pionnière de modèles de polyèdres réguliers en quatre dimensions !

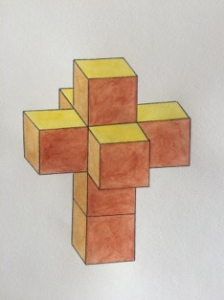
Figure 11. Alicia Boole et son patron d’hypercube.
Néanmoins il n’est pas très commode de suivre une chorégraphie sur un patron. Par exemple sur un cube, le développer sous forme de patron a l’inconvénient de couper les sommets de sorte qu’un même sommet se retrouve à plusieurs endroits sur le patron. Mieux vaut opter pour les conventions de perspective. On pense à un vecteur ayant quatre coordonnées, disons \((x,y,z,t)\), et on choisit quatre directions de projections, donc quatre vecteurs du plan \(u_1\), \(u_2\), \(u_3\) et \(u_4\). On représente alors \((x,y,z,t)\) par le point du plan donné par \(xu_1+yu_2+zu_3+tu_4\).
Ce qui donne par exemple, en dimension \(4\) :
La direction représentée en pointillés est celle correspondant à la quatrième danseuse. Ici il faut essayer bien plus de trois fois pour arriver au constat qu’il n’y a pas de code de Gray-Beckett. Il faut parcourir \(42\) possibilités ! Ou faire faire la recherche par un ordinateur. Quoi qu’il en soit, Quad ne peut être jouée avec ses contraintes initiales. D’où l’idée de lui trouver une grande sœur avec plus de danseur\(\cdot\)se\(\cdot\)s. Et, coup de chance, il existe des codes de Gray-Beckett cycliques pour \(5\leq n\leq8\). On les connaît même tous pour \(5\leq n\leq 6\).
Voici donc la pièce dansée que nous avons proposée lors des SurpreNantes Journées, ou plutôt la partie mathématique d’icelle, car la partie dansée pourrait également être codée (par exemple en notation Laban), mais c’est une autre histoire !
On a ici choisi deux directions supplémentaires : la quatrième et la cinquième dimension ! Maintenant qu’on les a repérées, il est plus commode de les effacer, puis de dessiner d’un coup tout le parcours.
Nous laissons les lectrices et les lecteurs se convaincre que c’est effectivement une solution au problème pour \(n=5\) !
Références
-
Samuel Beckett. Quad et autres pièces pour la télévision, suivi de L’épuisé par Gilles Deleuze. Paris : Les éditions de minuit, 1992. ↩
-
Fan Chung, Persi Diaconis et Ron Graham. « Universal cycles for combinatorial structures ». In : Discrete Mathematics 110 (1992), p. 43-59.
-
Mark Cooke et al. A note on Beckett-Gray codes and the relationship of Gray codes to data structures. ArXiv e-prints, 1608.06001v2. Août 2016.
-
Édouard Lucas. Récréations mathématiques. Paris : Gauthier-Villars, 1891. ↩
-
Joe Sawada et Dennis Chi-Him Wong. « A fast algorithm to generate Beckett-Gray codes ». In : Electronic Notes in Discrete Mathematics 19 (2007), p. 571-577.
François Sauvageot est professeur de chaire supérieure en classe préparatoire (MP*) et acteur de science populaire. Un extrait vidéo du spectacle Quadrature à cinq danseur\(\cdot\)se\(\cdot\)sest disponible ici.


Une réflexion sur « Quadrature »
Les commentaires sont fermés.