Sculptissimo
Deuxième art après l’architecture mais avant la peinture, la sculpture désigne étymologiquement l’art de tailler la pierre. Restrictive, cette définition a depuis évolué, incluant des techniques aussi variées que sont le modelage, l’assemblage, l’embossage ou la soudure. Ce faisant, elle s’ouvrait à d’autres matériaux : argile, plâtre, cire, métal, bois, verre, résines. Aujourd’hui tout à la fois plasticien, paysagiste, menuisier, potier, verrier, forgeron, le sculpteur se joue de la matière. Dans ses trois états il l’étire, la chauffe, l’ajoute ou la retire. Tout en faisant des sciences. En témoignent les outils et les procédés dont quelques observations, de simples activités récréatives [1] ou une sortie au musée [2,3] nous révèlent combien les mathématiques y sont esthétiques et indispensables.
Karim Zayana
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Quand « 0,3+30+40=39 », ou l’art d’être grand-père
Quand on n’a plus d’élèves ni d’enfants en âge de l’être… il reste ceux des autres ; et le temps mitigé d’un samedi d’automne… les Mako moulages. Exhumé du grenier, caché sous les petits soldats et les poupées plastique, le coffret recèle un trésor : des moules en silicone. Increvables malgré deux générations de maltraitances, ils n’ont pas pris une ride. C’est l’essentiel. La poudre de plâtre et les ustensiles se trouveront à la cave au rayon bricolage. La séance peut commencer quand, subrepticement, les mathématiques s’y invitent…
Étape 1 : faire le plâtre.
Aïe aïe aïe, il faut d’abord lire les notices, figure 1 ! Et ça commence très fort, « 1,5 doses d’eau pour 2 doses de plâtre ». Les mélanger dans une auge produit une solution crémeuse blanche. Pour la teinter en cyan comme sur le nuancier, on y verse quelques gouttes de colorant, à raison d’un « tube de 25 mL dans 2,5 L ». Avant personnalisation de détails au pinceau, cette opération donne un fond bleu aux tirages. Même ébréchés, ils le conserveront.

Figure 1. Nuancier (à gauche), notice (au centre), et plâtre teinté (à droite) obtenu avec un ratio 1 : 100 : 133 en colorant : eau : plâtre.
La conversion des millilitres en litre effectuée, nous comprimons ces informations dans un ratio \[1 \space :\space 100 \space :\space 133\]
Autant de pondérations qui reflètent une distribution : les parts volumiques respectives de pigment, de plâtre et d’eau à introduire. Par exemple 0,3 mL d’indigo concentré, 30 mL d’eau, et 40 mL de flocons de plâtre. Surprenante chimie, le volume de la somme des trois ingrédients ne sera pas l’addition de leurs volumes, soit les quelques 70 mL attendus, mais un peu moins de 40 mL ! Et pour cause, l’air se logeant entre les particules de plâtre est chassé par l’eau dont elles vont s’hydrater. Des liaisons de structure se créent, contractant l’ensemble qui, l’espace d’un quart d’heure, paraît encore fluide et malléable.
Une fois gâché, le plâtre redevient gypse en « prenant » progressivement puis il se fige, dur comme le roc. Dans l’intervalle, il aura de nouveau rétréci (à la marge), l’excès d’eau s’évaporant. 15 minutes, 14 minutes, 13 minutes,…, ne traînons pas, le compte-à-rebours est lancé !
Étape 2 : remplir les moules.
La membrane d’élastomère est un négatif. Elle comporte en creux le relief de la pièce à créer. Mathématiquement, nous dirions qu’elle en délimite le complémentaire, pareille à une frontière. Suspendue à l’envers sur des croisillons, on la remplit par sa base de plâtre liquide. Le modèle une fois sec est simple à délivrer puisque, flexible, le moule se retire comme une chaussette, figure 2.

Figure 2. Opérations de remplissage et de démoulage (les statuettes en plâtre sont pleines).
Le procédé fait merveille sur les figurines miniatures, même complexes. Avec des formes plus volumineuses et donc plus lourdes, le moule, trop souple, se déformerait : les répliques ne seraient plus fidèles. Pour le rigidifier, on l’emboîte dans une chape : sorte de gangue solide et amovible aux contours plus grossiers. En général, cette coque ne peut être d’un seul tenant : les angles rentrants empêcheraient de la retirer sauf à la « perdre » (c’est la terminologie) en la cassant. On la divise donc en plusieurs pièces (souvent deux, parfois plus) qui s’imbriquent les unes aux autres grâce à des tétons, ou clés, figures 3 et 4.
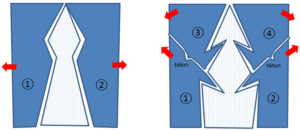
Figure 3. Vues simplifiées et en coupe d’un coffrage à deux pièces, et d’un autre à quatre pièces (deux tétons représentés ; lors du démontage, chasser d’abord les pièces inférieures). Les membranes de silicone, à l’interstice de la chape et de la pièce de plâtre endevenir, ne sont pas représentées.

Figure 4. Pièces éparpillées d’un coffrage complexe. Au centre : le positif qui sera obtenu. Musée Bourdelle, Paris.
On les assemble à la manière d’un puzzle tridimensionnel que l’on tapisse du silicone, en les maintenant fermement grâce à des sangles. Plus tard, on desserre l’ossature, on démonte et on dépouille. Tout peut être réutilisé, on dit que le moulage est « à bon creux ». L’épreuve garde la marque des plans de joints sous la forme d’étroits plis, les « coutures », qu’il suffit d’ébarber.
Étape 3 : et pour faire des œufs ?
Les personnages que nous obtenons par la méthode décrite ci-dessus sont pleins. Avec des moules en plexiglass on peut en fabriquer des creux (aux formes simples toutefois). Le plâtre liquide doit napper uniformément les parois intérieures de l’empreinte. Pour éviter toute accumulation par gravité, on utilise un moulinet centrifugeur, figure 5. L’appareil tient de l’essoreuse à salade et de la toupie gyroscopique. La grande roue rouge est fixe, montée sur un socle. Un cerceau médian, à l’intérieur, est mis en rotation par la manivelle. Il est à peine décalé afin d’intégrer un système d’engrenages le reliant au grand cadre. En tournant, son pignon engrène avec la denture de la couronne, imprimant un mouvement accéléré à l’un de ses diamètres, dont est solidaire le petit cercle jaune. C’est à ce dernier qu’on arrimera le moule.

Figure 5. Centrifugeuse à tournoiement. Le moule en plexiglass (non représenté) vient se placer entre les points d’arrimage. ③ tourne dans ② qui tourne dans ①.
Le rapport de transmission ramène les \(8\) dents du pignon aux \(80\) crans de la couronne, d’où un facteur multiplicatif de \(10\) ! À chaque tour de manivelle, tel un cosmonaute, le moule décrit une révolution autour de l’axe moteur, et, orthogonalement, \(10\) rotations sur lui-même.
« Et, dis, comment on fait le premier moule ? ». C’est un problème (résolu) d’œuf ou de poule. Sans œuvre originale, le « maître étalon », qu’on enduira de silicone, de gélatine, ou de plâtre par exemple pour faire son négatif, pas de moule. Sans cette matrice, pas de copie(s). L’artiste peut s’inspirer d’un objet réel, qu’il reproduit ensuite à l’échelle ou qu’il agrandit. Traditionnellement, et bien que la création, l’impression et le fraisage numériques soient passés par là, il travaille une matière qui se modèle, comme l’argile et certains plâtres ; qui se taille, comme la pierre ou le bois ; ou qui se plie, s’allonge et se frappe, comme le cuivre ou l’or. À l’opposé, en bout de chaîne, les statues en bronze d’un Rodin1 ou d’un Bourdelle2 et les résines fibrées de verre d’un Jeff Koons3 résultent d’un moulage.
Bricomathos
Pour façonner l’original, le sculpteur utilise des outils, dont quatre, liés à la mesure et au repérage, retiendront notre attention : le mètre, le compas, la coulisse et le pantographe.
Le mètre
Rien de plus banal qu’un mètre ruban, pourtant… Il possède en son extrémité un embout métallique en forme d’équerre. Cette encoche est rivetée, mais peut malgré tout se déplacer longitudinalement d’un petit millimètre, figure 6. Ce n’est pas parce qu’elle est mal fixée ! C’est pour tenir compte de son épaisseur et employer l’instrument aussi bien en poussée qu’en traction. Le premier centimètre du ruban ne compte en effet que 9 mm. En poussée, le bord extérieur de la languette est en contact avec le début de la pièce à mesurer : il indique le 0, le bord intérieur indiquant le 1 mm. En traction, le bord intérieur indique le 0 et le jeu de 1 mm déporte justement la lame à 1 mm. Ingénieux.

Figure 6. Détail d’un mètre à ruban et le secret de son crochet toujours bringuebalant.
La coulisse
On mesure précisément des sections avec un pied à coulisse. Aujourd’hui doté d’un affichage digital, sa mâchoire était jadis pourvue d’un vernier4 (et l’est toujours, dans les gammes de prix intermédiaires). Pour en comprendre le principe, il faut s’imaginer une pièce de diamètre \(d\), placée sous une règle graduée en millimètre. Nous avons \(d = N + \varepsilon\) avec toute la difficulté d’estimer \(\varepsilon\) à l’œil nu, figure 7. Plaçons contre la pièce et sous la règle, un réglet — le coulisseau — de 10 divisions dont la longueur est égale à 9 divisions de la règle, soit 9 mm. Plus resserrées, les graduations du coulisseau vont progressivement céder du terrain à celles de la règle, jusqu’à coïncider avec (au dixième de millimètre près). Il aura fallu parcourir autant de graduations de part et d’autre pour observer cet alignement, du reste facile à repérer de visu. En notant \(n\) leur nombre, il vient
\[\begin{aligned}
\varepsilon & = n – n \times \frac{9}{10} \textrm{ (en mm)} \\
& = \frac{n}{10} \textrm{ (en mm)}\end{aligned}\]
Ainsi, \[d = N + \frac{n}{10}\textrm{ (en mm)}.\]

Figure 7. Fonctionnement d’un pied à coulisse avec vernier, mesurant ici un diamètre d de \(N+ε≈N+ \frac{n}{10}\)= 16,6 mm au dixième de millimètre près.
Certains verniers, plus fins, comptent 20 divisions du coulisseau pour 19 mm de règle. La précision s’en trouve doublée. Les plus performants en ont 50 pour 49 mm, atteignant donc une résolution du cinquantième de millimètre, figure 8.

Figure 8. Pied à coulisse précis au cinquantième de millimètre.
L’« étrier »
À plat, l’intersection de deux cercles fournit au mieux deux points. Pourvu d’être localisé, même grossièrement, tout point du plan est donc précisément situé connaissant ses distances à deux autres points qu’on aura définis de base. On y pique le compas qu’on écarte des bonnes longueurs, on esquisse avec sa mine les deux arcs dans le lieu de recherche, ils s’y croisent au point cible. Le procédé se transpose à l’espace avec trois sphères. L’artiste choisit trois points de référence sur ou proche de l’objet réel qu’il prend pour modèle. Il les reporte sur sa selle de sculpture et bricole un squelette. Pour placer un quatrième point, il en mesure d’abord les distances aux trois points de base avec des compas de potier. Arqués, ces « étriers » peuvent enjamber les reliefs et pénétrer les anfractuosités, figure 9.

Figure 9. Panoplie de compas (« étriers ») à l’usage des sculpteurs et des potiers. Musée Bourdelle, Paris.
Puis l’artiste transfère ces mesures vers l’exemplaire qu’il modèle ou qu’il taille. La trace qu’y laisse le compas ressemble à trois arcs délimitant un triangle approximativement sphérique5, d’autant plus ramassé qu’on touche au but, figure 10.
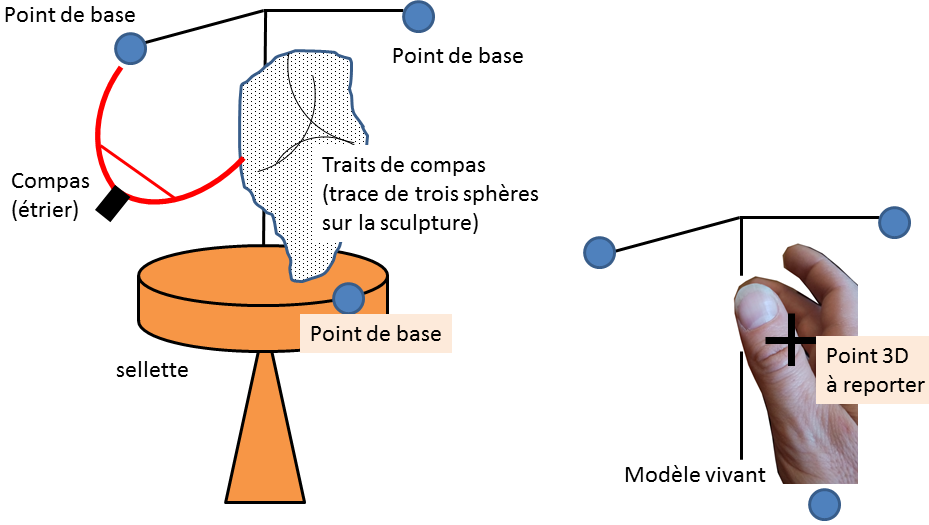
Figure 10. Mise aux points par la technique des trois compas.
Le compas permet également de contrôler toutes les symétries, en particulier des visages. On compare ainsi consciencieusement les distances entre les membres situés d’un côté (œil – oreille ; narine – commissure ; etc.) à celles situées de l’autre. Indispensable, largement utilisé pendant l’Antiquité par les Égyptiens et les Grecs, l’outil servit par exemple à Phidias6 pour exécuter ses sculptures en marbre.
Le pantographe
Le pantographe est un bras articulé, tournant sur lui-même et mobile de bas en haut. Il est équipé d’une sonde et terminé par une pointe. La sonde et la pointe, qui sont rivées à la perche, sont attelées l’une à l’autre pour rester parallèles. Bien proportionnées à l’écartement des rivets, elles définissent une configuration de Thalès. L’ancrage du dispositif et les deux appendices restent en permanence alignés, tout en dessinant une ligne semblable, dans son équilibre, à celle des rivets. La perche est comme rotulée à son pied, figure 11 (schéma de principe), puisque, concrètement, trois liaisons l’autorisent à
-
pivoter de bas en haut à la manière d’un canon qui s’élève et qui s’abaisse (mouvement de nutation, angle \(\psi\)) ;
-
s’orienter de gauche à droite à la manière d’une tourelle ou d’un hibou (mouvement de précession, angle \(\theta\)) ;
-
tourner sur elle-même à la manière d’une broche (mouvement de giration, ou de rotation propre, angle \(\varphi\)).
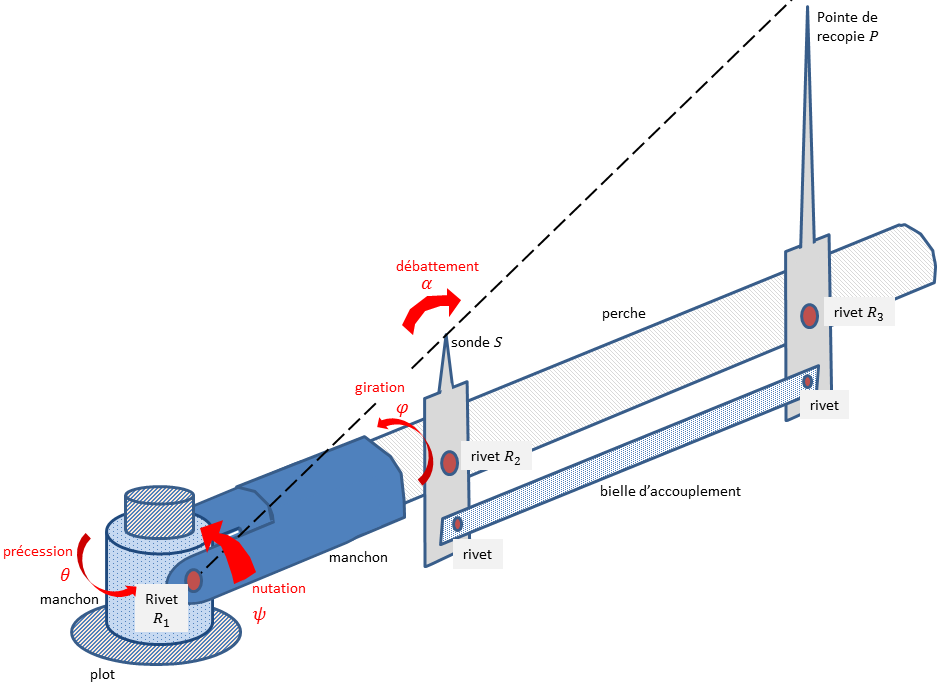
Figure 11. Schéma de principe d’un pantographe à quatre degrés de liberté. La condition de Thalès doit être vérifiée : \(R_2S\times R_1R_3=R_3P\times R_1R_2\). En toute rigueur, sur ce modèle simplifié, \(R_1\) bouge légèrement (il tourne de θ) et \(R_1\), \(R_2\), \(R_3\) perdent (à peine) leur alignement quand la perche tourne de φ dans son manchon.

Figure 12. Le sculpteur américano-belge Guillaume Werle réalise un agrandissement de L’Éternelle idole au pantographe, ici au musée Rodin de Meudon le 13 octobre 2019.
Grâce à ses quatre degrés de libertés (un angle de débattement \(\alpha\) et trois angles d’Euler7 \(\psi\), \(\theta\), \(\varphi\)), la sonde se meut avec aisance. Tout ce qu’elle détecte est communiqué à la pointe dans un rapport d’homothétie. Une fois positionné, le bras ne retombe pas : sur les plus petits dispositifs, les frottements s’y opposent quand les plus grands tiennent par un contrepoids (non représenté). En modelage, la pointe rencontre peu d’obstacles puisqu’il s’agit essentiellement d’adjoindre de la matière, figure 12. En taille, elle racle le bloc. La choisir souple ou rétractable peut régler cet inconvénient.
À force de va-et-vient, le mécanisme permet d’agrandir8 n’importe quel modèle, parfois dans des dimensions monumentales comme le fit César9 sur son célèbre pouce.
L’art et la mathière
Nous avons parlé du plâtre dans la partie Quand «0,3+30+40=39», ou l’art d’être grand-père. Polyvalent (il se modèle comme il se coule), bon marché et recyclable, ses atouts en font le chouchou des débutants. Évoquons maintenant l’argile, le bronze et l’or.
L’argile
Une fois malaxée, l’argile sèche lentement à l’air libre. Elle peut ensuite être cuite à haute température (1000°C) dans des fours appropriés. Si elles lui confèrent ses qualités définitives, ces opérations la contractent significativement, de l’ordre de \(r=10~\%\) dans chaque direction. Il faut préalablement évider la pièce, sans quoi elle s’écrase sur elle-même. Puis veiller à ce que l’épaisseur reste uniforme, sinon le séchage n’est pas homogène, causant fissures et cassures. Utilisée comme contenant (jarre, bol), la pièce doit avoir été calibrée en conséquence. Un retrait linéaire de \(r=10~\%\) réduit en effet le volume d’environ \(3r=30~\%\). Pour preuve, si \(\mathcal{V}\) désigne le volume enfermé par la pièce d’argile, devenue céramique son volume ne sera plus que de \[\mathcal{V}’ = \mathcal{V}.(1-r)^3\] Or \[(1-r)^3 \underset{r \to 0}{=} 1 – 3r + \mathcal{O}(r^2)\] Au regard de la valeur de \(r\), relativement modeste, \((1-r)^3 \simeq 1 – 3r\). Donc \[\mathcal{V}’ \simeq \mathcal{V}.(1-3r)\] et, pour des raisons assez voisines, \[\mathcal{V} \simeq \mathcal{V}’ .(1+3r)\] puisque \((1-3r)(1+3r) \underset{r \to 0}{=} 1 + \mathcal{O}(r^2)\).
Le bronze
Le bronze est un alliage d’étain et de cuivre, utilisé depuis la nuit des temps. Il ne se comporte pas comme une pâte qu’on étire, rompt et agrège à volonté. En sculpture, il est par conséquent coulé à chaud. Contrairement à ce qui se passe dans la partie Quand «0,3+30+40=39», ou l’art d’être grand-père, le moule qui l’accueille n’est pas un silicone entouré d’une coquille. Une telle empreinte ne résisterait pas au métal en fusion. On lui substitue une terre réfractaire, faite d’un mélange d’eau, de plâtre et de sable par exemple. Ce faisant, on édite d’abord un positif en cire à l’aide du négatif en silicone. On le borde de la terre réfractaire. Bouillant, le métal est extrêmement fluide. Or le moule ne doit pas fuir. À l’inverse de la méthode de la partie Quand «0,3+30+40=39», ou l’art d’être grand-père, on le fabrique donc le plus souvent d’un seul tenant, le perçant par endroits de micro-canalisations qui échapperont les gaz. Sec, il emprisonne la cire, qu’on ne peut plus évacuer qu’en la « perdant » par cuisson. À 200°C, celle-ci fond et sort par un orifice de coulée. Le même par lequel on verse le bronze, porté à plus de 1000°C. Après refroidissement, le moule est brisé, donc « perdu ». On dégage l’œuvre. Elle sera par la suite retouchée : limée, patinée, peinte.
Ainsi conçue, la sculpture est pleine. Pour alléger son poids, mais aussi son coût, on creuse le positif en cire qui prend l’aspect d’une pellicule solide. Ensevelie sous la terre réfractaire, elle en est aussi comblée, figure 13. On prévoit la quantité de bronze en fonction du volume \(\mathcal{V}\) à remplir une fois le décirage effectué.
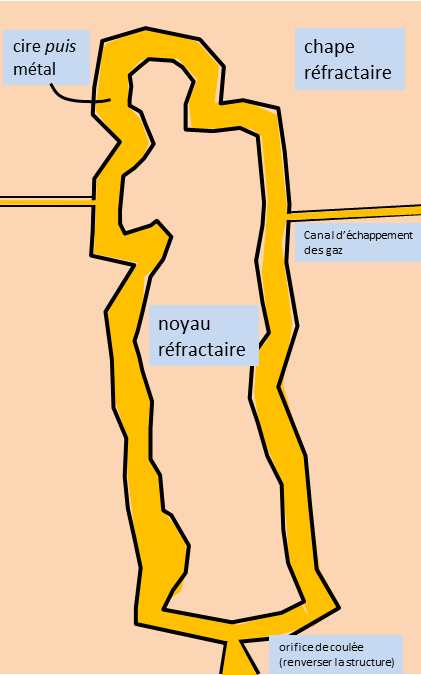
Figure 13. technique de la cire perdue sur une Vénus. Le moule est constitué d’une chape et d’un noyau ; la statue sera creuse.
-
Grossièrement, \[\mathcal{V} < a \times b \times c\] où \(a\), \(b\), \(c\) sont les cotes d’un pavé dans lequel l’œuvre s’inscrit ;
-
Plus précisément, \[\mathcal{V} < a \times b \times c – \mathcal{V}_N\] où \(\mathcal{V}_N\) est le volume du « noyau » couvert de cire, qu’on estime au moment de le maçonner ;
-
Plus exactement, \[\mathcal{V} \simeq S \times e\] où \(e\) désigne l’épaisseur de cire et \(S\) sa surface. On peut évaluer \(S\) en voilant l’original, ou en le bardant avec des bandelettes ;
-
Le plus simple reste… de remplir d’eau le moule à ras-bord (et de le vider ensuite) !
L’or
D’une beauté magnétique, qui ne s’est jamais extasié devant un tableau de Klimt10 ? On sublime ainsi certains ouvrages d’art en les ornant à la feuille d’or : ferronneries d’apparat, toitures grandioses, statues majestueuses, reliures et enluminures, pâtisseries d’exception, …, figure 14.

Figure 14. Dorures à la feuille d’or : grille royale du château de Versailles (Versailles), flamme de la statue de la liberté (New York), dôme des Invalides (Paris).
Très ductile, l’or s’étire et s’écrase pratiquement à l’infini. À cet effet, on utilise des petits laminoirs, des batteurs et des bancs de traction. On peut alors convertir un lingot d’un kilo, de la taille d’un téléphone (52 cm³) tant il est dense, en un long fil de diamètre 0,1 mm ou en une multitude de feuilles de 15 cm de côtés, à la finesse d’un dixième de micromètre. Dans le premier cas, la longueur du fil vérifie \[\pi \times \left(\frac{10^{-2}}{2}\right)^2 \times \ell = 52\] d’où la valeur de \(\ell\) en cm qui, une fois exprimée dans l’unité la plus appropriée, donne \[\ell \simeq 6,6\dots \text{km} \thinspace !\] Dans le second cas, le nombre \(N\) de films satisfait \[N \times 15^2 \times 10^{-5} = 52\] soit \[N \simeq {23000}\]
Au cours actuel, environ 40 000 € le kilo, le mètre de fil revient à 6 € et la feuille à un peu moins de 2 €. En joaillerie, la pureté de l’or se mesure en carat. À 100 % d’or massif correspondent 24 carats. Miscible à l’argent (mais aussi au laiton, au cuivre, …) il participe à des alliages dans lesquels sa contribution peut tomber jusqu’à 58 % de la masse totale (14 carats). Le nombre 24, qui rythme aussi le jour, comporte assez de diviseurs pour se fractionner aisément. Ainsi, 22 carats reflètent une proportion de onze douzièmes de masse d’or ; 20 carats de cinq sixièmes ; 18 carats des trois quarts.
En bonne hypothèse, les volumes d’or et l’argent d’un alliage d’« or blanc » s’ajoutent : de tailles comparables, les atomes des deux métaux s’échangent par substitution mais aucun ne s’insère dans les espaces du réseau cristallin de l’autre. La masse volumique du mélange en découle. Voyons comment. Les masses volumiques des deux métaux sont connues : \(\rho_{\mathrm{O}}=19,3\text{ g/cm³}\) pour l’or, \(\rho_{\mathrm{A}}=10,5 \text{ g/cm³}\) pour l’argent. Soit \(m_{\mathrm{O}}\) et \(m_{\mathrm{A}}\) les masses d’or et d’argent dans l’alliage, \(\alpha_{\mathrm{O}}\) et \(\alpha_{\mathrm{A}}\) leurs proportions respectives avec \(\alpha_{\mathrm{O}} + \alpha_{\mathrm{A}} = 1\), \(\mathcal{V}_{\mathrm{O}}\) et \(\mathcal{V}_{\mathrm{A}}\) les volumes associés. Les équations de conservation s’écrivent \[\left\{
\begin{array}{rclcl}
m& =& m_{\mathrm{O}}+m_{\mathrm{A}}& =& \alpha_{\mathrm{O}} m + \alpha_{\mathrm{A}} m \\[5pt]
\mathcal{V}& =& \mathcal{V}_{\mathrm{O}} + \mathcal{V}_{\mathrm{A}}& =& \dfrac{\alpha_{\mathrm{O}} m}{\rho_{\mathrm{O}}} + \dfrac{\alpha_{\mathrm{A}} m}{\rho_{\mathrm{A}}}
\end{array}
\right.\] La masse volumique \(\rho\) résultante apparaît comme une moyenne harmonique pondérée : \[\rho = \frac{m}{\mathcal{V}} = \frac{1}{\dfrac{\alpha_{\mathrm{O}}}{\rho_{\mathrm{O}}} + \dfrac{\alpha_{\mathrm{A}}}{\rho_{\mathrm{A}}}}\] ou encore \[\rho = \frac{\rho_{\mathrm{O}} \rho_{\mathrm{A}}}{\alpha_{\mathrm{O}} \rho_{\mathrm{A}} + \alpha_{\mathrm{A}} \rho_{\mathrm{O}}}\]
Par exemple, un or blanc à \(22\) carats exclusivement composé d’or et d’argent \(\left(\alpha_{\mathrm{O}} = \dfrac{11}{12}\text{ et }\alpha_{\mathrm{A}}=\dfrac{1}{12}\right)\) aurait, en appliquant cette formule, une masse volumique \(\rho_{22\text{ ct}}=18 \text{ g/cm³}\). Pour un or blanc à \(20\) carats, nous trouvons \(\rho_{20\textrm{ ct}}=17 \text{ g/cm³}\). Et pour un or blanc à 18 carats, \(\rho_{18\textrm{ ct}}=16 \text{ g/cm³}\). Ces valeurs obtenues par le calcul sont conformes aux tables dont se servent les marchands d’or. Elles permettent de contrôler le titrage d’un bijou et de traquer les contrefaçons. Plus précisément, sur la foi d’un alliage annoncé (or + argent seuls, pour simplifier), on mesure le volume \(\mathcal{V}\) de la bague, du collier, du bracelet, … avec une éprouvette et sa masse \(m\) avec une balance. On résout le système linéaire de deux équations à deux inconnues, \(\alpha_{\mathrm{O}}\) et \(\alpha_{\mathrm{A}}\) \[\left{
\begin{array}{rcl}
1& =& \alpha_{\mathrm{O}} + \alpha_{\mathrm{A}} \\[5pt]
\mathcal{V}& =& \dfrac{\alpha_{\mathrm{O}} m}{\rho_{\mathrm{O}}} + \dfrac{\alpha_{\mathrm{A}} m}{\rho_{\mathrm{A}}}
\end{array}
\right.]
On extrait la teneur d’or en carat, \(\alpha_{\mathrm{O}} \times 24\). Bien entendu, le test peut être complété d’autres vérifications, ajoutant au besoin d’autres équations quand on suspecte la présence d’autres métaux : réaction à l’acide nitrique, magnétisme, conductivité thermique, conductance électrique, etc.
Conclusion
À travers l’art nous voyons la beauté des sciences et l’étendue de leur vocabulaire. Angles d’Euler, compas, cylindres, homothéties, masse volumique, pantographe, parallélépipèdes, pied à coulisse, ratios, règle graduée, rotations, systèmes d’équations, taux d’évolution, etc. n’en sont qu’un bref aperçu. Mais il y a plus important. Comme le sculpteur, le professeur accomplit une œuvre devant sa classe, avec son tableau, à chaque heure de son cours. Son œuvre est unique, ni identique à la précédente ou à la suivante, ni parfaitement semblable à celle de ses collègues. Elle se crée dans l’instant et pour l’éternité dans la mémoire de ses élèves.
Remerciements
L’auteur remercie l’équipe d’Au fil des maths, pour sa relecture très détaillée, Guillaume Werle pour sa démonstration aux commandes du pantographe, ainsi que Romuald Zayana, designer industriel chez Carrefour (Massy) et Renaud Skrzypek, professeur de physique-chimie en MP* au lycée Hoche (Versailles), pour nos innombrables échanges aussi animés qu’interminables.
Références
-
Mako créations.. Consulté en novembre 2019.
-
Musée Rodin. Expositions permanentes des œuvres et des outils utilisés par l’artiste dans ses ateliers.
-
Musée Bourdelle. Expositions permanentes des œuvres et des outils utilisés par l’artiste dans ses ateliers.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Karim Zayana est inspecteur général de l’Éducation, du Sport et de la Recherche, ainsi que professeur invité à l’Institut Polytechnique de Paris (Palaiseau).
-
C’est aussi sur ce principe que fonctionne le GPS. Les trois points de base sont autant de satellites dont les distances au véhicule se déduisent des délais de transmission, appelés « temps de vol » (approximativement, à la vitesse de la lumière).
-
L’appareil peut également être utilisé en réduction, en échangeant les rôles de la pointe et de la sonde, avec notamment des applications possibles en microchirurgie.
-
Gustav Klimt : peintre autrichien, xixe – xxe siècles, dont le tableau « Le baiser » est devenu iconique.
