Assiette magique
Ce qu’on aime, avec Dominique Souder, c’est sa façon de faire feu de tout bois pour faire un peu de mathématiques tout en égayant notre vie quotidienne. Au menu du défi de ce jour : une table de restaurant pourvue d’une nappe en papier, et une attente un peu longue devant votre assiette encore vide. Découvrez comment tromper votre faim avec un simple crayon !
Dominique Souder
© APMEP Décembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Comment trouver le point diamétralement opposé d’un point situé sur le contour d’une assiette ?
Comment trouver le point diamétralement opposé d’un point situé sur le contour d’une assiette ?
Comment trouver le point diamétralement opposé d’un point situé sur le contour d’une assiette ?
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Enseignant de mathématiques aujourd’hui à la retraire, Dominique Souder se consacre désormais à des animations autour de la magie mathématique.
Pour citer cet article : Souder D., « Assiette magique », in APMEP Au fil des maths. N° 530. 8 janvier 2019, https://afdm.apmep.fr/rubriques/recreations/assiette-magique/.
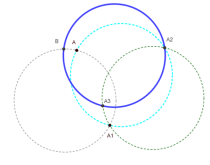
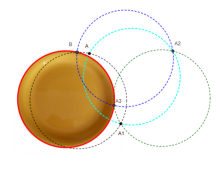
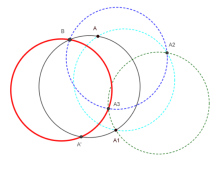
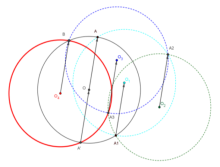
Une réflexion sur « Assiette magique »
Les commentaires sont fermés.