Décomposition des nombres en maternelle
Faire découvrir les nombres et leurs utilisations en cycle 1… Dans cet objectif, Laurence Le Corf nous expose son projet « Création d’un journal du nombre » en Grande Section.
Laurence Le Corf
© APMEP Décembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Les instructions officielles
Les nouveaux programmes insistent particulièrement sur la stabilisation de la connaissance des petits nombres. Voici un extrait du BO 2 du 26 mars 2015![]() :
:
Stabiliser la connaissance des petits nombres
Au cycle 1, la construction des quantités jusqu’à dix est essentielle. Cela n’exclut pas le travail de comparaison sur de grandes collections. La stabilisation de la notion de quantité, par exemple trois, est la capacité à donner, montrer, évaluer ou prendre un, deux ou trois et à composer et décomposer deux et trois. Entre deux et quatre ans, stabiliser la connaissance des petits nombres (jusqu’à cinq) demande des activités nombreuses et variées portant sur la décomposition et recomposition des petites quantités (trois c’est deux et encore un ; un et encore deux ; quatre c’est deux et encore deux ; trois et encore un ; un et encore trois), la reconnaissance et l’observation des constellations du dé, la reconnaissance et l’expression d’une quantité avec les doigts de la main, la correspondance terme à terme avec une collection de cardinal connu.
L’itération de l’unité (trois c’est deux et encore un) se construit progressivement, et pour chaque nombre. Après quatre ans, les activités de décomposition et recomposition s’exercent sur des quantités jusqu’à dix.
Un peu plus loin, le BO donne les attendus en fin de grande section :
Étudier les nombres
-
Avoir compris que le cardinal ne change pas si on modifie la disposition spatiale ou la nature des éléments.
-
Avoir compris que tout nombre s’obtient en ajoutant un au nombre précédent et que cela correspond à l’ajout d’une unité à la quantité précédente.
-
Quantifier des collections jusqu’à dix au moins ; les composer et les décomposer par manipulations effectives puis mentales. Dire combien il faut ajouter ou enlever pour obtenir des quantités ne dépassant pas dix.
-
Parler des nombres à l’aide de leur décomposition.
-
Dire la suite des nombres jusqu’à trente. Lire les nombres écrits en chiffres jusqu’à dix.
Je n’ai pas attendu la parution des programmes de 2015 pour travailler sur la décomposition des nombres, je le faisais déjà les années précédentes. Les nouveaux attendus de fin de maternelle m’ont juste confortée dans le fait de travailler cette notion en la ritualisant avec l’utilisation de supports pertinents.
Cette année, j’ai intégré dans ma circonscription un groupe expérimental sur la construction du nombre au cycle 1, mené par Pascal Percheron (IEN Saint-Brieuc-Est). Je travaille plus particulièrement la décomposition des nombres et la création d’un journal du nombre en m’inspirant de ce qui a été fait dans le cadre de la recherche ACE1 (Arithmétique et Compréhension à l’École élémentaire) au cycle 2.
Mise en œuvre en classe
Séance 1 : manipulation individuelle avec les boîtes à décomposer
Lors d’un atelier dirigé, je propose à chaque enfant une boîte à décomposer bleue avec deux compartiments, une ardoise Velleda et un feutre.
Il s’agit pour les élèves d’essayer, par exemple, de trouver toutes les façons de faire \(5\). Pour cela, ils placent les pions dans les compartiments et dessinent ensuite ce qu’ils ont trouvé. Ils travaillent individuellement.
Pour les premiers nombres, je ne leur dis pas le nombre de possibilités mais au delà de \(5\), je leur dis le nombre de boîtes à dessiner.
Je les aide lorsqu’ils me sollicitent et je garde une trace de leur recherche qu’ils retrouveront ensuite dans leur journal du nombre individuel.
Il est assez simple de différencier le travail : je peux faire quelques recherches avec un élève pour ensuite le laisser chercher seul, je peux demander à certains d’écrire sous les cases le nombre de pions, limiter le nombre de boîtes dessinées pour ne pas décourager les plus en difficultés.

Décomposition du nombre 5.
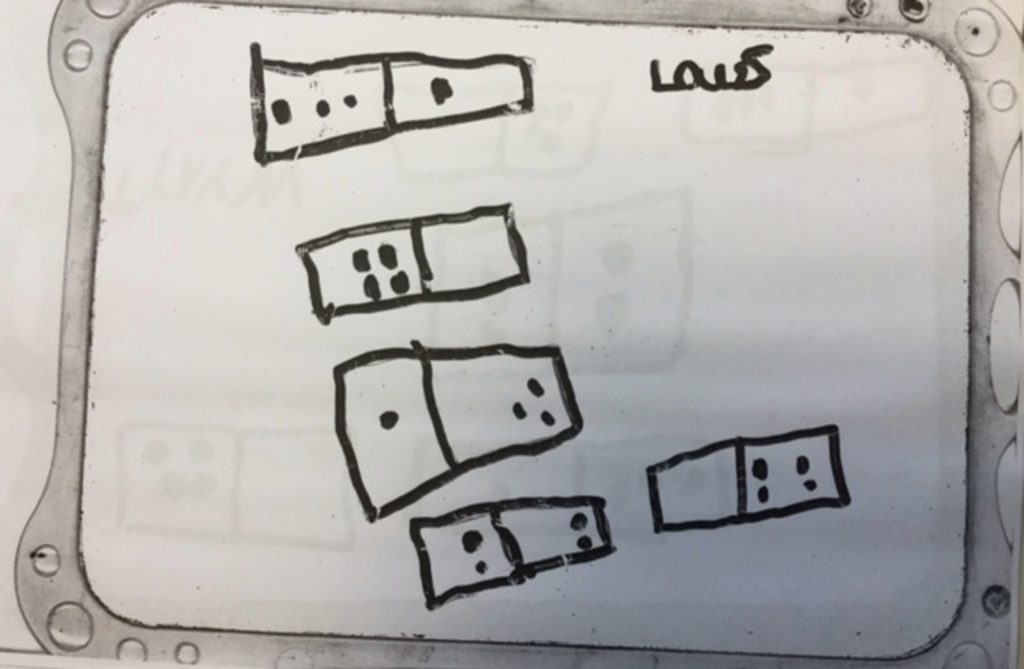
Décomposition du nombre 4.
Par la suite, ce travail pourra être repris en atelier autonome au cours de l’année.
Séance 2 : élaboration collective d’une trace écrite
Tous les élèves de la classe sont désormais dans le coin regroupement face au tableau. Avec des aimants et les dessins des boîtes à décomposer, ils viennent déplacer les aimants pour montrer leurs différentes propositions que le groupe classe valide ou non.
La manipulation des aimants est importante car elle permet de ne pas avoir tout de suite une trace définitive : on peut recommencer, discuter, valider ou non.
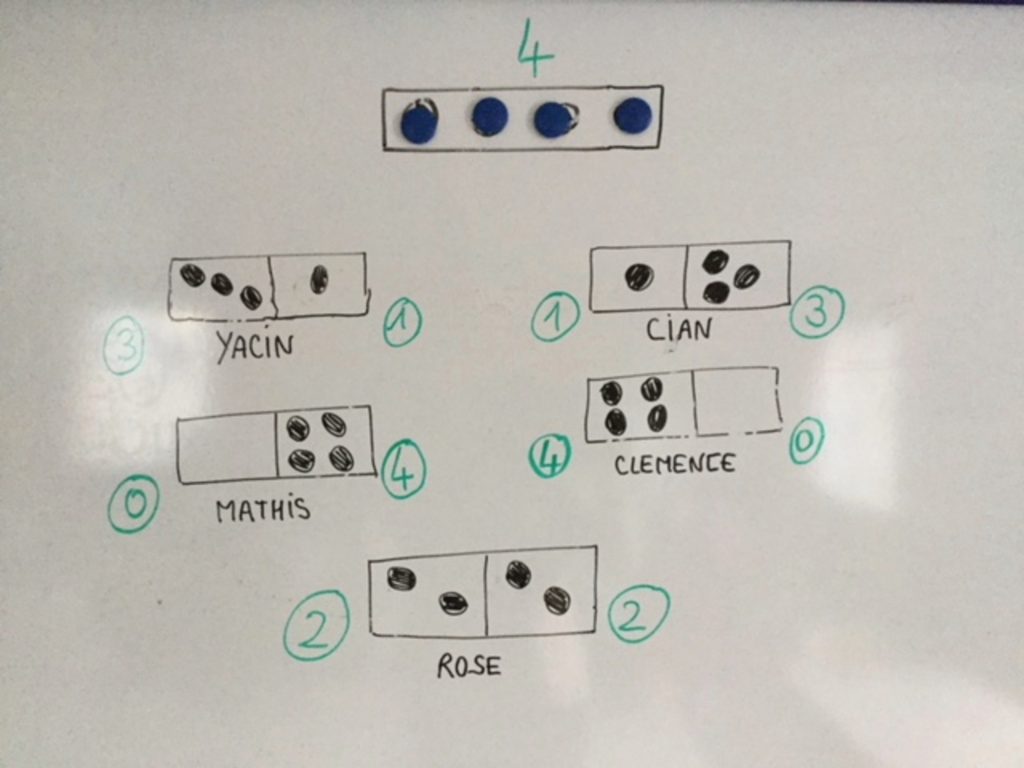
Décomposition du nombre 4.
Les élèves sont complètement partie prenante de leur apprentissage et surtout, les affichages de classe sont ainsi réalisés avec eux.
Depuis que je pratique ainsi, je trouve qu’ils réinvestissent plus facilement les affichages créés, notamment dans les diverse situations problèmes rencontrées.
Je garde une trace de cette séance en photographiant le tableau pour ensuite en faire une trace collective qui sera affichée sur le mur de la classe réservé à la connaissance des nombres. Cette fois, c’est moi qui fais la mise en page sur l’affiche car c’est le document référent (phase d’institutionnalisation). Il s’agit en fait de recopier au propre toutes les propositions trouvées collectivement sur le tableau.

Affichage dans la classe.
Séance 3 : travail individuel de réinvestissement, en atelier autonome
Sont mis à disposition des élèves : la boîte à décomposer bleue et des jetons si besoin (élément de différenciation : à ce stade, certains en ont encore besoin, d’autres pas), une feuille bleue format A5 et des papiers prédécoupés blancs (en fait deux rectangles comme les matrices de domino vierges).
Les élèves recherchent à nouveau toutes les façons de décomposer les nombres en utilisant ou non la boîte et en s’aidant si besoin de l’affichage collectif. Ils collent ensuite chaque décomposition sur la feuille bleue, feuille collée dans le journal du nombre dans un second temps.
Cette étape me permet d’observer les stratégies individuelles, de repérer les difficultés persistantes.

Production écrite d’un élève autour des décompositions du nombre 4.
Lors des séances, les élèves ont pour habitude de retourner la boîte bleue pour utiliser en acte la commutativité de l’addition (8 c’est « 3 et encore 5 » ou « 5 et encore 3 »). Une de mes élèves les plus fragiles m’a montré qu’elle trouvait les inverses en manipulant directement les pions dans ses mains qu’elle croise.

8 c’est « 3 et encore 5 » ou « 5 et encore 3 ».
Elle a montré aux autres sa stratégie lors d’un temps de bilan des activités.
Séances suivantes : création du journal du nombre
Afin d’avoir un support qui regroupe toutes nos activités autour de la décomposition du nombre, j’ai décidé de mettre en place un journal du nombre individuel.

Extrait du journal du nombre d’un élève.
Celui-ci retrace la démarche évoquée plus haut mais surtout permet aux élèves de se l’approprier bien au-delà des séances dirigées.
Chaque élève réalise son journal du nombre, qu’il complète et enrichit au fur et à mesure avec différentes façons de travailler la décomposition des nombres comme la peinture avec les doigts, les tampons, des collages d’objets…
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Laurence Le Corf est enseignante en grande section de maternelle et directrice de l’école maternelle Curie à Saint Brieuc (22). Elle est également PEMF (Professeur des Écoles et Maître Formateur) au sein de l’École Supérieure du Professorat et de l’Éducation (ÉSPÉ) de Bretagne, sur le site de Saint-Brieuc (22).
-
Le but de la recherche ACE-ArithmEcole, menée conjointement par plusieurs équipes de recherche issues d’académies différentes, est d’améliorer les pratiques pédagogiques en apportant une aide concrète aux enseignants afin de mettre en œuvre une progression des apprentissages mathématiques sur le nombre au CP et au CE1. Vous pouvez consulter les documents sur le blog de l’ÉSPÉ de Bretagne.
 ↩
↩


2 réflexions sur « Décomposition des nombres en maternelle »
Les commentaires sont fermés.