« Informathique »
Interdisciplinaire, mouvante et prolifique : elle a de quoi intimider. Pourtant l’informatique n’est pas une science occulte. Observée à travers le prisme des mathématiques, les auteurs nous invitent dans son univers. Ils y joignent de nombreux exemples codés en Python pour illustrer leur propos et éclairer le comportement, parfois étonnant, de l’ordinateur.
Karim Zayana et Edwige Croix
© APMEP Décembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
En lien avec les mathématiques de lycée[2], l’informatique offre un espace très ouvert à l’innovation et la réflexion pédagogiques. L’enseignant doit d’abord démêler ce qui relève du bon sens, de la culture commune, de la nouveauté, de l’analogie, du faux ami, de l’accessoire, du fondamental, de l’écueil, du palier didactique. Une fois ces champs bien identifiés et explicités pendant le cours, rien n’est impossible ni au professeur, ni à ses élèves. Car « à quinze ans, il y a une ardeur de l’intelligence qu’il importe d’attraper : comme certaines comètes, elle ne repassera plus » [1]. Nous aborderons ainsi les notions de variable (scalaire ou vectorielle), de fonction, de logique, de boucle et d’algorithme. Nous plongerons même au coeur de la machine pour tenter d’expliquer quelques phénomènes déroutants du langage Python.
Nous nous intéressons ici à quelques concepts clé de la science informatique, en dialogue avec les mathématiques. Nous aborderons ainsi les notions de variable (scalaire ou vectorielle), de fonction, de logique, de boucle et d’algorithme. Nous utiliserons parfois un vocabulaire métaphorique, aux dépens de la rigueur ou de la précision, ce pour varier les approches et rendre plus tangibles certains aspects délicats.
Variable ou Variable
La variable mathématique est un objet caméléon, une espèce de lutin aussi difficile à cerner qu’elle est immatérielle. Création de l’esprit, elle naît d’une étincelle, se simplifie d’une rature, se propage comme la foudre. Même astronomique, elle escalade sans peine un dénominateur ou se multiplie à l’envie. Espiègle lorsqu’elle voyage incognito, elle nous envoûte encore quand, transformiste, elle change d’aspect, de rôle, de nom. On la baptise \(x\) (de l’arabe « shay’ » «![]() », qui signifie « quelque chose »1, dont l’initiale « sh » phonétisée en « chi » a pour symbole grec \(\chi\)), \(y\), \(z\), \(M\), \(\varepsilon\)… Mais rien n’interdit d’utiliser les premières lettres de l’alphabet \(a\), \(\alpha\), \(b\), \(\beta\),… – on lui confère alors plutôt le statut de coefficient, variable statique en quelque sorte.
», qui signifie « quelque chose »1, dont l’initiale « sh » phonétisée en « chi » a pour symbole grec \(\chi\)), \(y\), \(z\), \(M\), \(\varepsilon\)… Mais rien n’interdit d’utiliser les premières lettres de l’alphabet \(a\), \(\alpha\), \(b\), \(\beta\),… – on lui confère alors plutôt le statut de coefficient, variable statique en quelque sorte.
La variable informatique n’hérite qu’en partie de ces qualités. Mieux personnalisée que sa consœur mathématique, il n’est pas rare de la nommer par un digramme voire par un mot complet : u0, tab, OuiNon, compteur. Exactement comme une propriété dans un cadastre, il lui faut s’enregistrer sur un « terrain » physique, plus ou moins spacieux – on parle de taille mémoire, cela à un endroit précis – on parle d’adresse mémoire. La taille dépend du type des données ; par exemple un booléen tient sur un bit2, un caractère sur un octet, un entier court sur deux, un réel, une adresse, un entier long sur davantage. De plus en plus, c’est la machine, et non le programmeur, qui s’occupe de l’allocation mémoire.
Variable scalaire
Quand un programme crée une variable réelle, appelons-la apy, l’ordinateur lui réserve quelque part, à une certaine adresse, un segment de la mémoire vive : le terrain, auparavant en friche, figure 1.
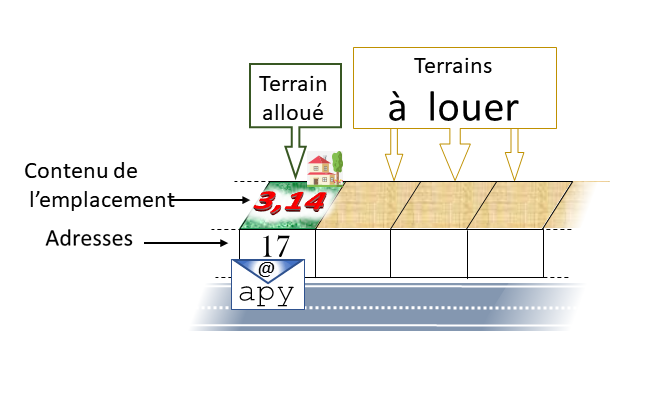
Figure 1. Happy pi.
Les initialisations et manipulations diverses vont ensuite le cultiver, pour contenir \(3\), ou \(3,125\) ou s’approcher de la valeur de \(\pi\) si tel était le but de l’algorithme3. Quand on refait tourner le même code, sur une autre machine, ou un peu plus tard depuis la même machine, l’implantation de apy aura changé : l’ordinateur l’aura certainement stockée ailleurs. Bref, une variable scalaire est un couple formé d’une adresse et d’une valeur, deux caractéristiques susceptibles de changer. Ajoutons qu’un processeur enchaîne les tâches séquentiellement, sans effet rétroactif, et nous serons en mesure d’expliquer certaines curiosités de l’informatique au regard des mathématiques.
Soit l’énoncé :
\(x=1\) ; \(y=x\) ; que vaut \(y\) ? ; \(x=0\) ; que vaut \(y\) ?
La variable \(x\) est introduite et se déguise en \(1\). Puis on déclare \(y\) liée à \(x\). Dès lors \(1\) est aussi le costume de \(y\). Ensuite \(x\) s’habille en \(0\). Donc \(y\) aussi. C’est ainsi qu’on remonte habituellement des calculs en algèbre. On modifierait \(y\) que cela se répercuterait tout autant sur \(x\). La rétropropagation est naturelle en mathématiques : dans la résolution d’un système \(2\times2\), lorsqu’on trouve \(x=1\), on remonte cette information pour déterminer \(y\). Si on se rend compte qu’on s’est trompé et qu’en fait \(x=0\), on corrige bien sûr \(y\) en conséquence.
Une transcription naïve de cette syntaxe donnerait, en langage Python :
x = 1 ; y = x ; print(y) ; x = 0 ; print(y)L’effet de ces instructions n’est pas tout à fait identique. Quand la variable y est créée, une adresse autre que celle de x lui est attribuée, sur le terrain de laquelle est repiqué le paysage de x. Le terrain de x est ensuite « jardiné ». Actualiser x n’impacte pas y dont la valeur demeure un \(1\). De même, une remise-à-zéro de y ne perturbe pas davantage x, figure 2.
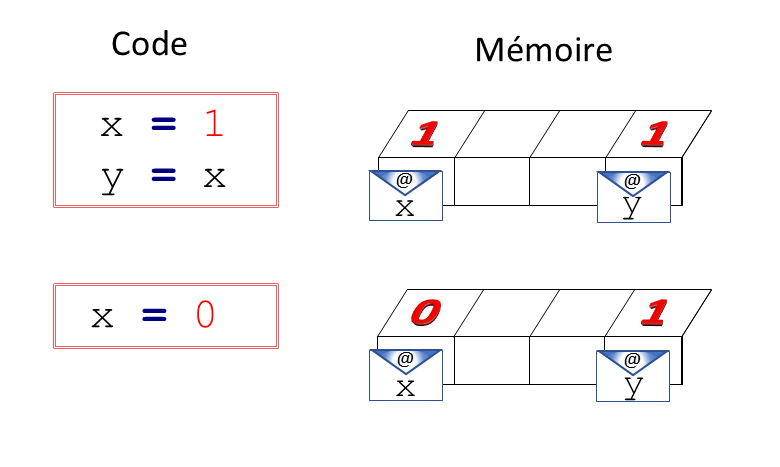
Figure 2. \(y=x\).
Le schéma est en réalité un peu plus complexe, mais cette vision, dont nous brosserons les possibles raffinements dans le paragraphe suivant, suffit à ce stade.
Tableaux et listes
Le tableau ou les listes sont, en apparence, les équivalents de nos \(n\)-uplets ensemblistes. Répétons l’expérience précédente. D’abord sous l’angle des mathématiques :
\(t=(10,15,-10,20,30)\) ; \(u=t\) ; que vaut \(u\) ? ; \(t_0=2018\) ; que vaut \(u\) ?
En bout de ligne, la variable \(u\) aura épousé les variations de \(t\) : \(u=(2018,15,-10,20,30)\).
Interrogeons Python :
t = [10,15,-10,20,30] ; u = t ; t[0]=2018 ; print(u)Surprise : u qu’on croyait immuable affiche [2 018,15,-10,20,30] après cette série de commandes4. De même, retoucher la copie u d’un tableau t altère d’autant l’original5. Cette fois, u et t sont interdépendants, comme de « vraies » variables mathématiques. La cause en est à la fois logique et subtile car elle demande de comprendre une machine et la façon dont elle a été conçue. On peut en donner plusieurs niveaux de lecture, approchant de plus en plus fidèlement ce que Python fait ou est susceptible de faire. Ils sont tous hérités du langage C et seront introduits par couches successives [4].
À la définition (ici en extension) du tableau t, l’ordinateur réserve un lotissement de 5 emplacements contigus en RAM à partir d’un certain endroit, chacun de la taille d’un entier. C’est cet endroit que référencie t. Donc : la variable t mobilise une première adresse. À cette adresse, étendue sur le terrain, on lit une deuxième adresse, par exemple (et, typiquement), assez lointaine de la première. En file indienne on y trouvera l’élément d’indice \(0\) du tableau, soit la valeur \(10\) (et, un peu plus tard, \(2018\)) ; la valeur \(15\) à côté ; la valeur \(-10\) ensuite ; et cætera, figure3. En somme, la variable t est un triplet (adresse ; adresse ; valeurs).
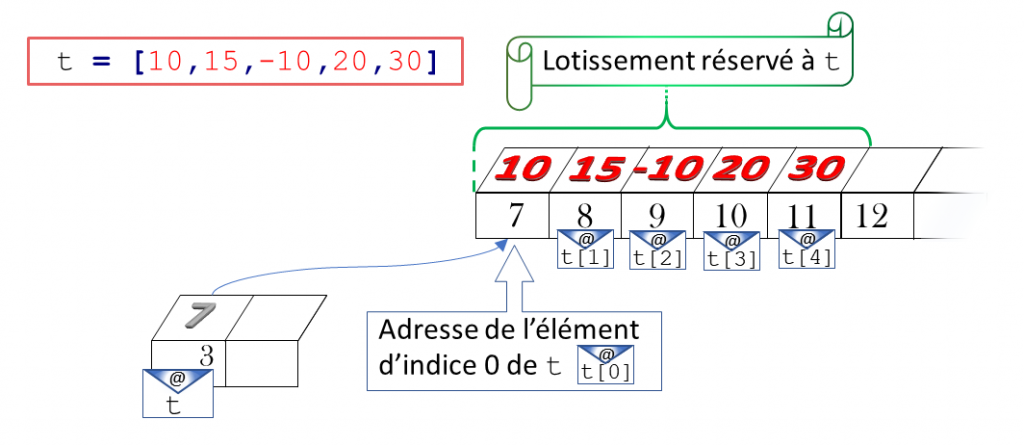
Figure 3. Le tableau t préempte le n° 3 puis s’étend en pointant vers le n° 7, adresse attribuée à t[0] qui a la valeur 10.
Arrive la variable u, qui se veut une réplique de t. On ne va pas tout recommencer ! Tant que les tableaux ne comportent que \(5\) cellules, cela va encore… mais imaginez des tableaux beaucoup plus grands, à un million d’entrées. Définir t et tout ce qui s’ensuit occupe déjà du temps et de la mémoire. Refaire ce travail pour u (réserver \(1\) million de nouvelles cases, transplanter une à une celles de t vers celles de u) serait déraisonnable. Il existe une parade. L’ordinateur empile u sur t : typiquement, il place u à une adresse proche de celle de t. Sur le terrain de u, il inscrit l’adresse de t[0], figure 4. Techniquement, u et t pointent vers le même tas. Concrètement, si perturbant cela soit-il, u diffère de t tandis que u[0] et t[0] sont identiques6. Et pour cause, t est, exhaustivement, le triplet (3 ;7 ;(10,15,-10,20,30)) et u, le triplet (5 ;7 ;(10,15,-10,20,30)). Quand on ressème les parcelles où sont implantées les valeurs t[0], t[1], t[2], t[3], t[4], cela rejaillit sur u. Et vice versa. La commande u=t est un peu aux tableaux ce que le raccourci bureautique est aux fichiers et dossiers informatiques.
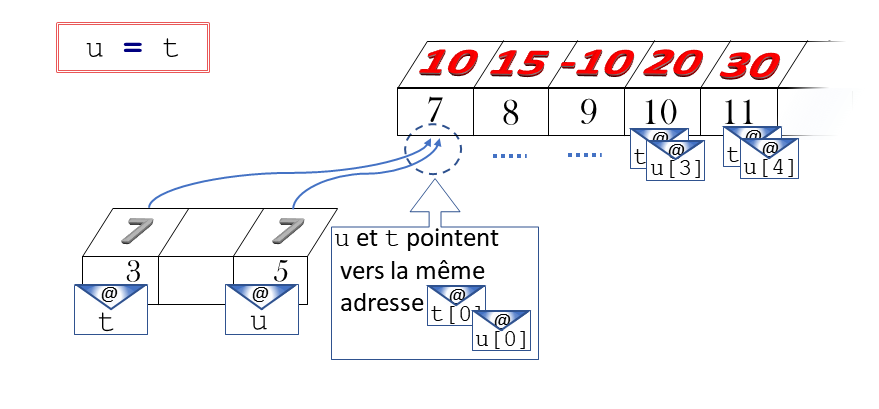
Figure 4. \(u=t\).
La manière précédente d’organiser7 les données est économique. Cependant, elle est peu flexible. Une fois les cellules mémoires écrites, il est possible de les regraver… à condition de ne pas les faire déborder, donc uniquement avec des données de même taille. Un terrain prédestiné à supporter une maisonnette (ici, l’entier 10 pour t[0]) ne peut recevoir ensuite un hôtel (un réel par exemple). Python saura dépasser cette rigidité du C. En ouvreuse avisée, Python replace t[0]. Si bien que t[0], t[1], t[2], t[3], t[4] vont inéluctablement s’éparpiller (quand bien même elles seraient de même type, dans les faits). Matériellement, t référencie une adresse, l’entrée d’un lotissement qui lui est réservé. À cette adresse, à la queue leu-leu, sont sauvegardées les adresses de t[0], t[1], t[2], t[3], t[4] auprès desquelles on cherchera leurs valeurs, collection hétéroclite d’objets : entiers, réels, caractères, chaîne de caractères, image, etc. figure 5. En quelque sorte, notre variable est un quadruplet (adresse ; adresse ; adresses ; valeurs).
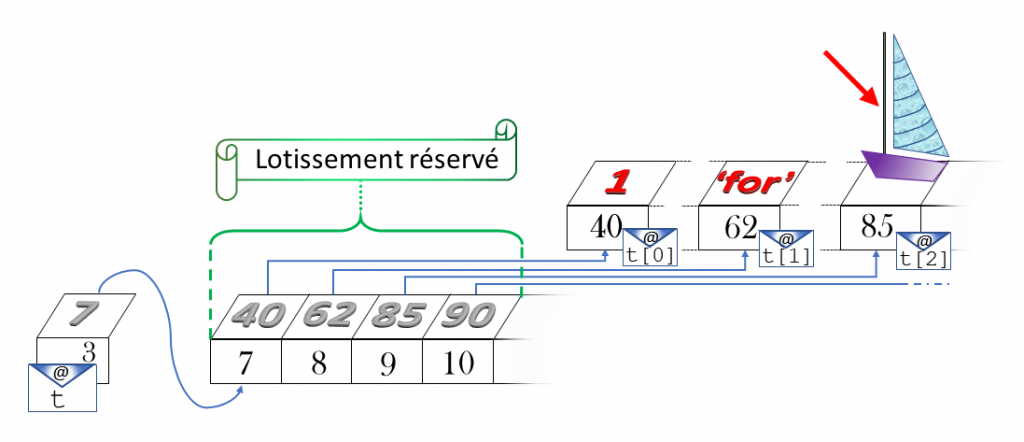
Figure 5. Tableau Python : Un-« for »-mât. . . ique.
Cette gestion de la mémoire est très pratique pour consulter un élément, par exemple t[3]. Le processeur y accède directement en reconstituant son adresse : en C, celle de t[0] à laquelle il additionne8 \(3\), soit 7+3 (il sait que ce 3 représente en vérité \(3 * 2\) octets s’il manipule des entiers courts, \(3 * 4\) voire \(3 * 10\) s’il s’agit de réels) – figure 3 ; dans les langages plus évolués, celle inscrite à l’adresse 7+3 (il sait que ce \(3\) représente en vérité \(3 * 8\) octets s’il manipule des adresses sur 64 bits) – figure 5. Puis il va voir. Mais il y a un mais. Insérer un terme entre t[2] et t[3] paraît facile. Dans le premier cas par exemple, il « suffirait » de tout décaler d’un cran à partir de t[3]. Ce faisant, on s’épuise en copies (nombreuses sur un grand tableau). Et, quelque précaution que l’on prenne, on finit toujours par produire un conflit, en écrasant la cellule destinée à recevoir t[5] dont rien ne garantit qu’elle était disponible. Si elle ne viole pas la mémoire, la suppression d’un élément ne dispense pas des fastidieuses recopies. Les informaticiens ont donc créé la structure de liste chaînée, plus souple, illustrée en figure 6 : une liste lc remplie des objets 1 (nombre), ’for’ (chaîne de caractères), mât (image), etc.
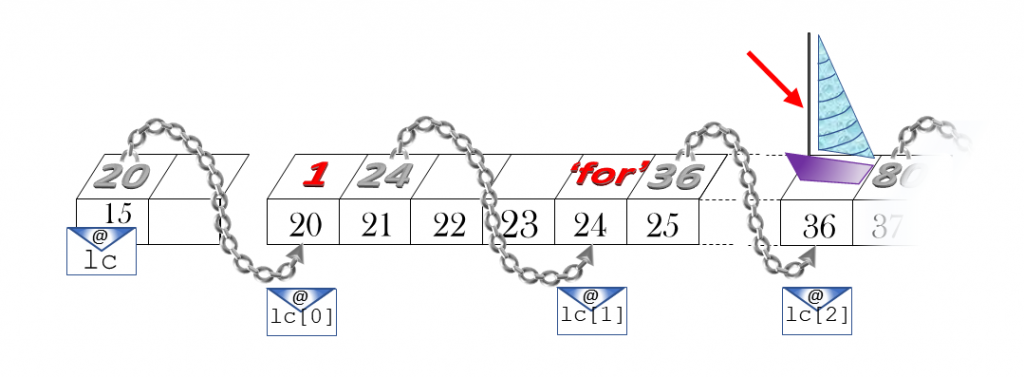
Figure 6. Liste chainée : Un – ’for’ – mât… que ».
Chaque cellule pointe vers la suivante, que l’ordinateur alloue au fur et à mesure (on dit « dynamiquement ») selon les espaces vacants qu’il trouve. Fragmentées, les données nagent un peu partout. Cela prend plus de place car il faut conserver une adresse par chaînon. Cela complique l’accès, et donc la recherche, d’un élément, car il faut faire défiler tous ses prédécesseurs. Mais à l’inverse, l’ajout d’un maillon ou la concaténation de deux listes par exemple se résolvent instantanément par simple redirection d’un pointeur.
Récapitulons. On peut se représenter un tableau rudimentaire comme un tas de cartes empilées. La première carte porte une valeur, mettons le \(10\). La suivante porte une autre valeur, mettons le \(15\). Celle d’après le \(-10\). Viennent enfin le \(20\), le \(30\), etc. Une liste chaînée, quant à elle, suit un parcours. La première carte porte le 1 au recto. Et le verso révèle le lieu où se cache la deuxième : dans ma poche. Au recto de la deuxième carte figure ’for’, au verso là où se trouve la suivante : sur le bureau. Le recto de la troisième carte dévoile la photo d’un bateau, le verso l’emplacement de la suivante : sur la lampe du tableau. Etc. Chic, une chasse au trésor !
Fonctions
Comme son nom l’indique, une fonction doit servir à quelque chose. Transformer du sucre en du caramel, râper du gruyère, changer du plomb en or, renvoyer \(x^2+x+1\) à partir de \(x\), calculer \(f’ ;\) connaissant \(f\), retourner9 [10,15,-10,20,30] en répondant [30,20,-10,15,10], etc. C’est donc très utile une fonction. Exemple codé :
def maFonction(x) :
return(x**2+x+1)Dans le langage écrit courant, on met plutôt \(x\) à gauche, à droite son image \(y\), et la flèche de \(x\) vers \(y\) surmontée d’un \(f\) minuscule place par conséquent \(f\) à droite de \(x\) : \(\quad x \xrightarrow{f} y\quad\). Il ne serait donc pas absurde de noter plus méthodiquement \(x(f)\) l’image \(y\) de \(x\). Certains élèves ont naturellement ce penchant, indésirable en mathématiques, mais qui mène à la convention d’écriture x.f() tout à fait admise en informatique10.
Dans la vie courante, une fonction consomme les ingrédients. Cela n’est pas le cas en mathématiques, où manufacturer \(f(x)\) ne détruit pas \(x\). En informatique, cela dépend des cas, c’est-à-dire de l’input. Voyons dans quelle mesure.
Quand on passe un argument en paramètre d’une fonction, cette dernière commence par en faire une copie locale, et c’est ce duplicata qu’elle va utiliser. Soit par exemple f(x,t) une fonction dépendant d’une variable scalaire x et d’une variable vectorielle (un tableau) t. Une fois appelée, f copie x et t. Elle crée donc x_local, et sur son terrain repique ce que contient x : un nombre réel. Puis elle crée t_local, et sur son terrain implante ce que contient t : une adresse. Puis elle ne traite plus qu’avec x_local et t_local. C’est sans danger sur x. En revanche, t et t_local désignent le même lotissement. Accéder aux cases indexées par t_local et les ré-écrire touche aussi t. Vérifions-le sur une fonction décalant circulairement de \(k \) positions un tableau. Elle procèderait11 comme suit :
def shiftLeft(k,t) :
n = len(t)
while k>0 :
temp = t[0]
for i in range(n-1) :
t[i] = t[i+1]
t[n-1] = temp
k = k-1
return(None)
t = [2018,15,-10,20,30]
k = 2
shiftLeft(k,t)
print(t) ;print(k)Comme prévu, k n’a pas bougé. Tandis que t représente [-10,20,30,2018,15]. On dit que t a été modifié en place.
En mathématiques, les fonctions se composent. En informatique, elles s’imbriquent comme des poupées gigognes. Dans un autre style de programmation, la fonction shiftLeft(k,t) pourrait résulter de deux modules : une première fonction décale d’une unité à gauche, une seconde appelle la première \(k\) fois. Signalons enfin qu’une fonction informatique n’a pas toujours d’argument, ou ne fabrique pas toujours le même résultat : pensons à random() et randint(1,6).
Logique et connecteurs logiques
Le branchement conditionnel en informatique tient de l’implication mathématique, où une prémisse induit une conclusion. Il peut s’avérer plus compact à implémenter qu’on ne le croît. Par exemple, quand on désire renvoyer la valeur absolue de \(x\), il suffit d’écrire
def valeurAbsolue(x):
return(2*(x>=0)-1)*xPlutôt que
def valeurAbsolue(x):
if x>=0:
return(x)
else:
return(-1*x)En effet, le booléen x>=0, qui vaut False ou True, est automatiquement apparenté à \(0\) ou \(1\) suivant les cas et donc 2*(x>=0)-1 vaut \(-1\) ou \(1\).
Certaines conditions sont parfois multifactorielles. Introduire les conjonctions « et » et « ou » par le couplet du fromage et du dessert oblige à discuter des « ou » inclusif (le « or ») et exclusif (le « xor », traduit par le dilemme « soit…soit…»). On pourra faire un autre parallèle, avec la circuiterie électronique. Et retenir que :
-
le « ou » logique fonctionne comme un système d’alarme : n’importe lequel des boutons du dispositif, qui sont câblés en parallèle, peut déclencher la sonnerie en faisant contact, figure 7.
-
le « et » logique fonctionne comme sur une machine sécurisée (une presse d’emboutissage, un taille-haie) : il faut appuyer simultanément sur deux boutons (câblés en série) pour être sûr qu’on n’y laisse pas de main, figure 8.
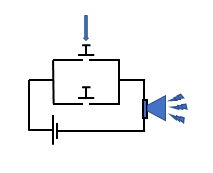
Figure 7. Schéma Ou. |
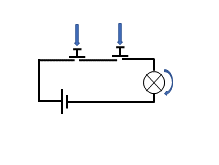
Figure 8. Schéma Et. |
Boucles
C’est un classique de la boucle « for », un tantinet impérative :
for k in range(5) :
print("Moi president")C’est un classique de la boucle « while », plus démocratique :
elu, k = 'o', 0
while (elu == 'o') :
print("Moi president (oui = o) ?")
k, elu = k+1,input()
print("Moi president", k,"an(s)")On relève à cet endroit le symbole distinctif « == » réservé au test d’égalité, quand le symbole « = » sert à l’affectation. Cela évite une polysémie, courante mais parfois gênante en mathématiques. L’affectation est orientée : le membre de droite vient habiller celui de gauche. Sur une calculette, elle est souvent rendue par une flèche12 : k \(\leftarrow\) k+1 par exemple. Il faut se garder d’une interprétation fonctionnelle, mathématiquement tentante mais à contre-sens, où « k+1 deviendrait k » et donc k, k-1 quand c’est en vérité k qui doit accueillir, donc devenir k+1.
On pourrait peaufiner l’interface homme-machine, ici très basique : gérer la casse (o minuscule et O majuscule), faire répéter la question quand l’utilisateur ne répond ni par oui ni par non. Tels ne sont pas les objectifs poursuivis ici ; nous considérons que l’utilisateur s’astreint au cahier des charges. Revenons au sujet :
L’ordinateur ne fait, lui, pas de différence sensible entre la boucle « for » (dite inconditionnelle, ou bornée) et la boucle « while » (dite conditionnelle, ou non bornée), qu’il traduit toutes deux à l’aide d’étiquettes (labels) et de sauts (goto).
Dans le premier cas, dans un pseudo BASIC, certes un peu aride, mais plus proche de la machine :
k = 0
Label Etiquette_1
Ecrire('Moi president')
Incrementer k
If k<5 Goto Etiquette_1Dans le second :
k = 0
Label Etiquette_1
Ecrire('Moi president (oui = o) ?')
Lire toucheRenvoyée
Incrementer k
Si toucheRenvoyée == 'o' Goto Etiquette_1
Ecrire('Moi president',k,'an(s)')Les deux paragraphes suivants instancient boucles, conditions et tableaux dans deux cas d’école.
Dic(h)otomie
L’exploration dichotomique mime la démarche d’un humain qui recherche un mot dans un dictionnaire, le mot «macaron» par exemple. On situe d’abord « macaron » par rapport au milieu. Puis on circonscrit nos efforts à la moitié qui le contient (la première dans un Larousse de poche). On recommence. Etc. L’étau se resserre jusqu’à tomber sur notre «macaron», ou faire chou blanc si le mot, trop savant, n’y figure pas (dans notre édition, il y figure).
Le Nombre Mystère est une autre activité, tout droit tirée des cours de récréations.
- « Je pense très fort à un nombre, entre 0 et 999 999, c’est le nombre d’amoureux(ses) que j’aurai. Tu le devines ! ». (252 018)
- « Plus petit que 100 000 ? ». « Non ».
« Que 200 000 ? ». « Non ».
« Que 300 000 ? ». « Oui ».
« Que 210 000 ? ». « Non ».
« Que 220 000 ? ». « Non ».
Etc.
De la gauche vers la droite, un peu, beaucoup, passionnément, les chiffres se stabilisent. Ce n’est pas, à proprement parler, une dichotomie : c’est davantage une « décachotomie » ; on divise en 10, puis on affine en redivisant en 10 le segment où prospecter, et ainsi de suite. Les calculs sont plus simples pour notre cerveau13. Si la dichotomie a eu tant de succès, c’est peut-être qu’elle est plus pratique pour Sieur l’ordinateur : diviser par deux un nombre codé en binaire revient à en décaler sa virgule vers la gauche.
La poêle à frire
Nos enfants ont grandi, ils sont maintenant au lycée.
- « f est une application (connue mais quelconque) de {0, 1, 2, . . ., 999 999} dans lui-même. Je pose u0 = 0, u1 = f(u0), u2 = f(u1), etc. ».
- « La suite des itérés, en somme! Elle boucle à partir d’un certain rang. Et pour cause, il n’y a « que » 1 000 000 d’images distinctes possibles. J’imagine cela comme une poêle ou un détecteur de trésor : en alignant u0, u1,. . . jusqu’au premier terme up qui réapparaîtra : c’est le manche. À partir de là, cela se répète : c’est le contour circulaire de la poêle ou de la bobine de détection – figure 9. Tu saurais déterminer p ainsi que le cycle ? ».
- « Mmm. Il y a une solution compliquée et coûteuse, où tu testes si chaque nouvel uk appartient à l’ensemble constitué de ses prédécesseurs. Et il y a une solution simple et habile où tu tiens à jour la liste des entiers déjà atteints dans un tableau t. »
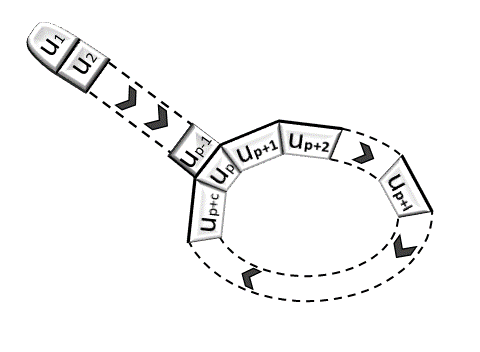
Figure 9. La poêle à frire.
Et oui ! On déclare d’abord un tableau t de \(n\) cases (avec \(n=1 000 000\)), toutes initialisées à \(0\), sauf t[u0] (ici t[0]) qu’on initialise à \(1\). Dès qu’on calcule un nouvel \(u_k\), on se reporte en case t[u] avec u=\(u_k\). Si la case est encore nulle, on la relève à \(1\). Sinon, c’est que la suite, telle un vinyle rayé, radote et nous jouera inlassablement le même passage. Une boucle « while » ainsi conçue détecte le terme \(u_p\). Une fois \(u_p\) connu, on fait calculer \(u_{p+1}\), \(u_{p+2}\),… jusqu’à recroiser \(u_p\). Bref, un autre petit while, contenant une liste cycle dans lequel on stocke les u via la méthode cycle.append(u) et la boucle est bouclée, code ci-dessous.
On observe le phénomène de la poêle à frire dans le développement décimal d’un nombre rationnel. Durant l’algorithme de division, les restes possibles s’épuisent et finissent par se rejouer. La suite des décimales qui en résulte est ultimement périodique.
def pseudoPeriode(n,u0) :
t = numpy.zeros(n)
t[u0] = 1
u,p = f(u0),1
while t[u] == 0 :
t[u] = 1
u,p = f(u),p+1
cycle = [u]
u = f(u)
while cycle[0] != u :
cycle.append(u)
u = f(u)
return(p-len(cycle), cycle)Algorithme ou programme ?
Il n’y a pas de honte à ne pas savoir ce qu’est un algorithme, puisque c’est un Monsieur, disparu depuis longtemps. On aura beau y voir une euphonie, algorithme ne dérive pas de « rythme », pas plus de « logarithme », ni même de « logos ». Il tire son origine du mathématicien Bagdadi, M. El Khawarizmi (IXe siècle). L’article défini « El », qui signifie « le » – comme il existe des « Legendre », « L’Hôpital », « Laplace » ou « Lagrange », s’infléchit en français en « Al », et le « Kh » se prononce comme une jota espagnole, approximativement rendue par un « g » guttural.
Convenons qu’un algorithme est un schéma de pensée dictant une chaîne causale et non ambigüe de tâches à réaliser. Une recette de cuisine est par exemple un algorithme. Le programme en est sa version machine. Il est précis au gramme14 près. Une lettre, un espace, une virgule, une tabulation, un zeste de ceci ou de cela, en trop ou en moins et, non de non, il ne tourne plus rond. Le programme informatique doit aussi composer avec la réalité : un espace de représentation limité, une mémoire bornée, un temps fini. D’où quelques aberrations imposant la plus grande vigilance.
Parfois, l’algorithme ne termine pas, mais le programme si. Deux exemples avec des réels, le « lilliputien » et le « doubleur fou » :
x = 0.5
while (x != 0.0) :
x = x*xx rapetisse tellement que l’ordinateur le confond avec 0 après une douzaine d’itérations. Il s’échappe alors de la boucle.
x = 2.0
while (x + 1 > x) :
x = x * xx grandit tant que l’ordinateur doit changer de braquet, sacrifier un bit de précision pour gagner un facteur d’échelle. Au lieu de compter de 1 en 1, il compte de 2 en 2, puis de 4 en 4, de 8 en 8 voire de 16 en 16 s’il le faut. Il ne peut alors plus discerner x de x + 1 après sept itérations.
Inversement, l’algorithme peut terminer, mais pas son programme. Exemple du « planteur de choux », inoffensif s’il calculait juste :
x,pas = 0,0.1
while (x != 1) :
x = x + pasIl raconte des salades et fait planter l’ordi. Le problème tient à la représentation machine du nombre 0,1. Remplacer pas par 0,125 (à savoir \(\dfrac{1}{8} = 2^{(-3)} \)) résout le paradoxe.
Pour preuve, enfin, que Python n’a pas livré, ici, tous ses secrets, testez ce dernier script et comparez :
t = [10,15,-10,20,30] ; u=t ; t = [2018,15,-10,20,30] ; print(u)En guise d’approfondissement, on consultera les références [2] et [4].
Les auteurs tiennent à remercier Robert Cabane, Vincent Pantaloni et Matthieu Le Floch pour leur relecture attentive et leurs fructueuses remarques.
Bibliographie
-
Amélie Nothomb. Le Voyage d’Hiver. Albin Michel, 2009. ↩
-
Eduscol. Algorithmique et programmation, ressource Eduscol pour le lycée.
 ↩
↩ -
François Boucher. « Autour de la multiplication des flottants ». In : bulletin de l’APMEP Au fil des maths n° 527 (2018).
 ↩
↩ -
Brian W. Kernighan et Dennis M. Ritchie. Le langage C. Dunod, 2014. ↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Karim Zayana est inspecteur général, professeur invité à l’Institut Mines-Télécom (Paris).
Edwige Croix est professeure de mathématiques et d’informatique au lycée Baggio (Lille).
Cet article fait suite à plusieurs échanges avec des étudiants du lycée Baggio (Lille) et avec les équipes de professeurs de Cayenne, Kourou, Saint-Laurent du Maroni (juin 2017-juin 2018).
-
Le diminutif « shuayya » (un petit quelque chose) est entré dans la langue française sous la forme « chouïa » .↩
-
Identifié à 0 (False) ou 1 (True), en pratique il occupe un octet : un processeur ne sait adresser que des blocs de 8 bits.↩
-
La valeur exacte est hors d’atteinte de l’ordinateur : seuls les nombres dyadiques, sommes finies de puissances (positives ou négatives) de deux le seraient [3]. Même \(1/10\) et même \(3,14\) ne sont pas à sa portée ! En revanche \(3,125\) l’est car il vaut \(2^1+2^0+2^{(-3)}\).↩
-
Un ordinateur donne des ordres.↩
-
Heureusement, ce n’est pas le cas en art… Au Louvre, la Joconde gardera le sourire !↩
-
Soit :
u\(\neq\)ttandis queu[0]=t[0]au sens de l’égalité mathématique et non de l’affectation informatique. Nous y reviendrons plus loin.↩ -
Un ordinateur ordonne.↩
-
Un ordinateur calcule (compute).↩
-
Où ce mot prend tous ses sens.↩
-
Sans entrer dans les détails, cette convention d’écriture s’appelle une méthode sur l’objet x.↩
-
Procédure et fonction sont à peu près synonymes en informatique.↩
-
Selon les constructeurs, la flèche est ou a pu être orientée autrement. Mais les deux conventions restent équivoques.↩
-
En effet, on a dix doigts… Certes, on a aussi pile deux mains.↩
-
« Gramme » signifie « lettre, inscription » en grec ancien.↩

Une réflexion sur « « Informathique » »
Les commentaires sont fermés.