Cercles discrets
François Boucher nous propose une promenade — historiquement datée : essentiellement les années 1960-1980 — dans quelques problèmes de tracé d’objets géométriques — essentiellement notre vedette du moment : le cercle — en mettant en évidence le rôle de mathématiques par ailleurs élémentaires : un peu d’arithmétique, de géométrie, d’analyse et beaucoup d’algèbre.
François Boucher
© APMEP Décembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Notre intention est d’illustrer le fait qu’algorithmique, programmation et mathématiques peuvent faire bon ménage à un niveau élémentaire à travers l’étude du problème « comment faire tracer un cercle sur un écran de pixels ? ».
L’attribution nominative des algorithmes peut être incertaine ; les algorithmes considérés sont assez simples pour avoir été produits simultanément et indépendamment, et tout n’a pas été publié ; de plus, la toile n’est pas très fiable en la matière1.
Quelques conventions
-
On adopte — avec la caution de Bourbaki — le principe « quand c’est strict, on le dit » ; ainsi « \(x\) positif » signifie \(x \geqslant 0\) et \(x>0\) signifie « \(x\) strictement positif ».
-
On utilise les écritures suivantes2 : pour \(x\) réel,
-
\(\left\lfloor x \right\rfloor\) désigne le plus grand entier inférieur à \(x\), alias la partie entière de \(x\) ;
-
\(\left\lceil x \right\rceil\) désigne le plus petit entier supérieur à \(x\) ;
-
\([x]\) désigne le plus grand entier plus proche (au sens de la distance usuelle sur \(\mathbb{R}\)) de \(x\).
Une reformulation de iii. est précieuse : \([x]\) est le plus grand entier3 \(n\) qui minimise \(|x-n|\) (l’ambiguïté qui nécessite de choisir le plus grand n’apparaît que dans le cas où \(x\) est un demi-entier.)
On vérifie que \([x]=\left\lfloor x+\dfrac{1}{2}\right\rfloor\), ce qui valide les propriétés : \(x \longmapsto [x]\) est croissante, continue à droite, et \(x \longmapsto [x]-x\) est \(1\)-périodique.
-
-
On adopte le vocabulaire informatique de Gilles Dowek ([3]) en parlant, pour une fonction, d’arguments formels (resp. d’arguments réels) pour désigner les variables abstraites qui apparaissent dans l’entête de définition, (resp. leurs valeurs lors d’un appel de la fonction).
Modèle
On travaille dans le plan \(\mathbb{R}^2\) et on prend \(\mathbb{Z}^2\) comme modèle très idéalisé de la grille de pixels d’un écran non borné (pas de sous-pixel, pas de couleur : du noir (pixel « allumé » !) et du blanc (pixel « éteint »). Pour les dessins éventuels, on représente \(\mathbb{Z}^2\) par un réseau de points à mailles carrées (ce qui revient à supposer que les pixels sont carrés). Une droite du réseau est une droite d’équation \(x=p\) ou \(y=q\) avec \(p\) et \(q\) entiers.
On peut représenter un pixel par un (gros) point ou un carré plein ; l’adresse d’un pixel est le centre du pixel. Le pixel (\(\texttt{px}\)) est aussi une unité de longueur (de l’ordre de quelques dixièmes de millimètre selon les écrans), et l’unité d’aire correspondante est le pixel carré (\(\texttt{px}^2\)).
Historiquement les algorithmes de tracé de droites et de cercles ont été conçus pour répondre aux problèmes d’affichage sur les écrans cathodiques (puis à cristaux liquides), d’impression matricielle, de numérisation par scanner et de commande des tables traçantes. A priori, allumer des pixels sur un écran et piloter une table traçante semblent des problèmes bien distincts, mais il s’agit bien de problèmes similaires, la plume d’un traceur avançant par pas.
Les objets géométriques de \(\mathbb{R}^2\) sont dits idéaux ; toute projection dans \(\mathbb{Z}^2\) d’un objet idéal est dite discrétisée4.
La principale question étudiée est celle des discrétisations d’un cercle euclidien dont le centre est \((0,\,0)\) et le rayon entier, et de quelques propriétés de cette représentation.
On divise le plan (\(\mathbb{R}^2\)) en huit octants (non disjoints), numérotés de 1 à 8 dans le sens «trigonométrique», le premier étant \(0 \leqslant y \leqslant x\). Tout tracé obtenu dans un octant peut être complété par des symétries au plan tout entier. L’utilisation de ces symétries se conçoit bien pour les tracés sur écran, mais est peu pertinente dans le cas d’un traceur.
On souhaite produire des algorithmes valides (resp. des programmes corrects), étudier leur complexité, si possible les optimiser…
Pour les petits programmes proposés, on utilise le langage Python 3.6.x et son module turtle pour sa simplicité d’emploi et sa lenteur qui permet d’observer le fonctionnement des algorithmes. Pour rendre les pixels visibles, on simule un zoom \(\times 4\) ou \(\times 8\). Et pour rendre les programmes lisibles, on évite d’utiliser trop de sucres syntaxiques pythoniens.
Dans les années soixante, il n’y avait pas encore d’unité de calcul d’arithmétique flottante intégrée ; pas de multiplication, de division ou de fonction \(\sqrt{\bullet}\) câblées, et encore moins de fonctions trigonométriques. La mémoire se mesurait en kilooctet (à un dollar l’octet) et la vitesse des processeurs en fraction de mégahertz. Il suffit de rappeler que l’ordinateur (haut de gamme) avec lequel travaillait Bresenham5 avait 16 ko de mémoire. Le prix à payer pour l’efficacité était de calculer sur des entiers en n’utilisant que des additions ou soustractions, et multiplication et division par deux avec un code le plus concis possible.
Un segment avec des entiers
On commence par étudier le problème plus simple du segment discret afin d’illustrer quelques méthodes de l’informatique : invariants et preuve de programme, transformations de programme, analyse de complexité.
On se familiarisera ainsi avec les problèmes rencontrés par les informaticiens de l’époque, et les solutions qu’ils ont imaginées.
Segments discrets algorithme de Bresenham
|
On cherche à tracer le segment joignant l’origine \((0,\,0)\) à l’adresse \((a,\,b)\) avec \(0 \leqslant b \leqslant a\) et \(a\), \(b\) entiers, \(a\) non nul. |
On pourra vérifier que ces contraintes ne sont pas restrictives : des symétries et une translation permettant de gérer tous les cas.
Donnons une heuristique géométrique de l’algorithme. Sur chaque droite verticale du réseau (donc d’équation \(x=i\)), on cherche le pixel le plus proche du point d’intersection avec le segment. La droite considérée a pour équation
\(bx-ay=0\)
On cherche à allumer les pixels les plus proches de la droite ; or la distance euclidienne de cette droite à un point \((x_0,\,y_0)\) est \(d=\dfrac{|bx_0-ay_0|}{\sqrt{a^2+b^2}}\) donc est proportionnelle à \(\left|\dfrac{b}{a}\,x_0 – y_0\right|\). Si \(x_0\) est entier, alors un entier \(y_0\) qui minimise \(\left|\dfrac{b}{a}\,x_0 – y_0\right|\) est précisément \(y_0=\left[\dfrac{b}{a}\,x_0\right]\). En posant \(h=\dfrac{b}{a}\) on allume donc les pixels situés aux adresses \(\left(i,\,[hi]\right)\) pour \(i\in[\![0,\,a]\!]\).
Un programme itératif s’écrit directement6 (programme 1).
| Fonction segment_1 |
from math import floor"""affiche les pixels(x,[b/a*x]),0<=x<=a"""h=b/ay=floor(h*x+1/2)return(None) |
Il s’agit ensuite de transformer ce programme en un programme uniquement en nombres entiers ; la solution proposée par Bresenham revient à rechercher une définition récurrente des \([hi]\) pour obtenir ce qu’on appelle un programme incrémentiel : un pixel étant allumé, quel est le suivant ?
Cette interrogation est naturelle dans le cas du pilotage d’un traceur : la plume étant à l’adresse \((x_i,\,y_i)\), quelle est la position suivante ?
En posant \(u_i=[hi]\), on observe que \(u_{i+1}\) égale \(u_i\) ou \(u_i+1\) (puisque \([x]\leqslant[x+h]\leqslant[x+1]=[x]+1\)) ; si le pixel \((i,\,u_i)\) a été allumé, le suivant sera \((i+1,\,u_i)\) ou \((i+1,\,u_i+1)\) ; pour choisir, il suffit de tester lequel est le plus proche de la droite idéale, en utilisant la (pseudo-)distance \(d(x,\,y)=|bx-ay|\). On cherche donc le signe de \(d(i+1,\,u_i)-d(i+1,\,u_i+1)\) ;
comme \(d(i+1,\,u_i)+d(i+1,\,u_i+1) <0\), le signe est aussi celui de
\(d^2(i+1,\,u_i)-d^2(i+1,u_i+1)\)
Un calcul simple assure que cette quantité est égale à
\(a\left(2(i+1)b – (2u_i+1)a \right)\)
En introduisant la suite
\(\delta_{i+1}=2(i+1)b-(2u_i+1)a\)
on a alors :
\[\begin{aligned}
i \in [\![0,\,a-1]\!]\quad u_{i+1}&= \begin{cases} u_i & \textrm{ si } \delta_{i+1} <0 \\ u_i+1 &\textrm{ sinon } \end{cases} \\
i \in [\![1,\,a-1]\!]\quad \delta_{i+1}&=\begin{cases} \delta_i+2b &\textrm{ si } \delta_i<0 \\ \delta_i+2(b-a) & \textrm{ sinon}
\end{cases}\end{aligned}\]
suites initialisées par : \(u_0=0\) et \(\delta_1=2b-a\) ; mais il est habile d’introduire l’élément initial \(\delta_0=-a\) qui permet de valider la récurrence précédente aussi pour \(i=0\).
La suite des pixels à allumer est donc la suite \(\left((i,\,u_i)\right)_{i \in [\![0,\,a]\!]}\) définie par les relations de définition ci-dessus et les valeurs initiales \(u_0=0\) et \(\delta_0=-a\).
Il est intéressant de chercher à démontrer à partir de ces définitions que \(u_i=\left[hi\right]\). Le lecteur pourra constater la difficulté de raisonner par récurrence sur \(i\) sans connaître la relation entre \(u_i\) et \(\delta_i\).
Un programme Python
pixel() est une fonction allumant le pixel passé en argument ; elle n’existe pas en Python mais peu importe pour l’instant le code correspondant (voir l’annexe).
Quelques commentaires s’imposent. On introduit deux constantes, trois variables informatiques i, u, delta, et une boucle conditionnelle plutôt qu’une boucle inconditionnelle pour mieux mettre en évidence le processus de preuve du programme qui suit, ce qui explique l’introduction de la variable i ; les boucles inconditionnelles cachent l’initialisation du compteur, initialisation importante dans la preuve.
À la ligne 5, on utilise une affectation simultanée : le tuple7 de droite est évalué, puis affecté au tuple (c,d) ; pouvoir omettre les parenthèses est un sucre pythonien.
Le return(None) terminal n’est pas indispensable et n’est mis que comme principe de « bonne programmation » ; la fonction Bresenham_seg renvoie effectivement la valeur None et agit par effet de bord sur l’écran (comme une procédure).
L’écriture d’un programme général traçant le segment discret joignant \((a,\,b)\) à \((c,\,d)\) n’est pas si simple…
| Exemple de code |
def Bresenham_eg(a,b) :"""droite discrete joignant (0,0) à (a,b)"""i = i + 1delta = delta + celse :delta = delta + dpixel(i,u)#POSTCONDITION : |

Bien que cela ne soit pas nécessaire puisque l’algorithmique a fait le travail, on propose une preuve informatique de ce programme. Rappelons qu’il s’agit de démontrer que, pour tout jeu d’arguments réels corrects (c’est à dire satisfaisant la pré-condition), le programme se termine et qu’il est correct, c’est-à-dire qu’il fournit ce pour quoi il a été conçu (la postcondition). Pour la mise en œuvre de cette preuve, nous suivons les principes de [2].
La spécification du programme Bresenham_seg est :
-
Pré-condition : \(a \in \mathbb{N}^{\ast}\) et \(b \in \mathbb{N}\) et \(b \leqslant a\) ;
-
Postcondition : les pixels situés aux adresses \(\left(i,\,[\dfrac{b}{a}\,i]\right)\) pour \(i\in [\![0,\,a]\!]\) (et seulement eux) sont allumés.
Pour le prouver, on introduit les éléments de preuve suivants :
-
la condition d’arrêt : \(i = a\)8 ;
-
les deux prédicats qu’on appelle des invariants9 :
\(I_1\) \(\delta=2(i+1)b-(2u+1)a\)
\(I_2\) \(\begin{cases} \left\{i=-1 \textrm{ et } u=0 \right\} \\ \textrm{ ou } \\ \left\{u=\left[\dfrac{b}{a}\,i\right]\textrm{ et }\right.
\textrm{pour tout } j \in [\![0,\,i]\!]\\
\qquad\qquad\left.\texttt{ pixel}\left(j,\,\left[\dfrac{b}{a}\,j\right]\right) \textrm{ allumé}\right\} \end{cases}\) -
la progression : les lignes 10-16 du programme ; on suppose ce code correct10 ;
-
la terminaison (ou le variant) : \(a-i\).
Premier point à valider : condition d’arrêt vérifiée et invariant vrai implique la postcondition.
Ensuite, on vérifie que l’initialisation « amorce » les invariants. Avec \(i=-1\) et \(u=0\), on a bien
\(2(i+1)b-(2u+1)a=-a=\delta\)
et le deuxième invariant est banalement vrai.
Puis vérifions que la progression conserve les invariants (d’où leur appellation) ; désignons classiquement par \(i’ ;\), \(\delta’ ;\) et \(u’ ;\), les valeurs de \(i\), \(\delta\) et \(u\) après exécution de la progression.
On a : \(i’ ;=i+1\) ; puis, si \(\delta<0\), alors \(\delta’ ;=\delta+2b\) et \(u’ ;=u\) ; on vérifie alors que
\[\begin{aligned}
2(i’ ;+1)b-(2u’ ;+1)a&=2(i+1)b-(2u+1)+2b\\
&=\delta’ ;\\[-35pt]\end{aligned}\]
Ensuite
\(\left[\dfrac{b}{a}\,i’ ;\right]=\left\lfloor \dfrac{b}{a}(i+1)+\dfrac{1}{2} \right\rfloor=\left\lfloor \dfrac{2b(i+1)+a}{2a} \right\rfloor\)
or \(2(i+1)b-(2u+1)a<0\) donc \[\dfrac{2(i+1)b+a}{2a}<u+1\]
et comme \(u+1\) est entier, on a \(\left\lfloor \dfrac{2(i{+}1)b{+}a}{2a} \right\rfloor\leqslant u\) ;
par ailleurs, \(x \longmapsto [x]\) est croissante, donc
\(\left[\dfrac{b}{a}\,i’ ;\right] \geqslant \left[\dfrac{b}{a}\,i\right]=u\)
D’où l’égalité.
D’autre part, si \(\delta \geqslant 0\), alors \(\delta’ ;=\delta+2(b-a)\) et \(u’ ;=u+1\) et on vérifie de même, que les deux invariants (sur les valeurs primées) sont vrais ; on utilise pour cela la précondition \(b \leqslant a\).
Puisque pixel\((i’ ,u’ )\) est allumé, on a bien pour tout \(j \in [\![0,\,i’ ;]\!],\, pixel\left(j,\left[\dfrac{b}{a}j\right]\right)\) allumé.
Reste la terminaison : chaque exécution de la progression diminue la terminaison de \(1\), qui atteint donc la valeur \(0\) en \(a+1\) étapes. Le programme se termine bien sur la validation de la condition d’arrêt et des invariants. Le programme est démontré.
Le cœur de la démonstration est la validation des invariants qui s’apparente tout à fait à une démonstration par récurrence (sur \(i\)) ; on y voit bien leur rôle essentiel.
Transformations d’un programme
Le programme 2 a été obtenu par voie algorithmique en travaillant sur des suites donc en se plaçant dans les mathématiques. Il est intéressant de savoir qu’on peut aussi l’obtenir par dérivation du programme [Prog1] à l’aide de modifications successives essentiellement syntaxiques proches des réécritures algébriques courantes des mathématiques ; en gérant en même temps la transformation des invariants, on obtient un programme validé.
On démarre avec le programme [Prog1] ; on suppose les calculs sur les rationnels exacts bien que cela ne soit pas le cas en Python. On transforme d’abord la boucle pour en boucle tant que ; on n’écrit pas tous les invariants et on travaille uniquement avec le corps de la fonction.
x,h=0,b/ay=floor(h*x+1/2) |
On observe ensuite que le produit h*x peut être calculé de façon incrémentielle en introduisant une nouvelle variable z = h*x ce qui permet de transformer une multiplication en addition.
x,h,z=0,b/a, 0y=floor(z+1/2) |
On introduit ensuite la nouvelle variable \(t=z+\dfrac{1}{2}\cdotp\)
x,h,t=0,b/a,1/2y=floor(t) |
On élimine ensuite l’utilisation de floor ; pour cela, on décompose t=te+tf en partie entière et partie fractionnaire. Il faut alors traiter l’incrémentation t=t+h selon que tf+h est plus grand ou non que 1.
x,h=0,b/apixel(x,te)te=te+1else:tf=tf+h |
Reste enfin à éliminer le 1/2 de l’initialisation de tf et l’utilisation de h ; pour cela, il suffit d’introduire la variable TF = 2 a tf ; comme le test tf+h>=1 devient 2atf+2b>=2a, il vaut mieux introduire la variable entière d=2b+2(tf-1)a. On obtient alors le programme 3.
Ce programme (que l’on pourrait encore peigner un peu) n’utilise que des entiers ; c’est essentiellement le programme Bresenham. Il est d’ailleurs intéressant de chercher à aboutir au programme 2 en déplaçant l’instruction pixel.
| Fonction segment_2 |
defsegment(a,b):d=2*b-apixel(x,te)te=te+1else:d=d+2*breturn(None) |
Complexité
Historiquement le point de vue pratique est premier ; l’analyse11 d’un algorithme (supposé correct) consiste à déterminer les ressources nécessaires à l’exécution d’une implantation sur une machine : mémoires, temps d’exécution, bande passante… afin de répondre à trois questions principales (et très pratiques) :
-
l’algorithme envisagé (disons plutôt une instance du programme le traduisant12…) peut-il effectivement fonctionner sur le matériel disponible ?
-
de deux algorithmes solutions du même problème, lequel est le plus efficace ? C’est le point important.
-
existe-t-il un algorithme optimal (en un sens à préciser) pour résoudre un problème donné ?
|
On va se préoccuper uniquement de ce que l’on appelle la complexité temporelle. |
Cette unité peut être un cycle d’horloge, la seconde, une opération particulière.
On choisit ensuite une mesure de la taille des données, c’est à dire une application \(t\) de l’ensemble des données \(\mathscr{D}\) dans \(\mathbb{N}\) ; a priori, il n’est pas exclu de mesurer la taille des données par un \(n\)-uplet, mais à ce niveau, on se contente d’un seul entier. Le point important est que la mesure de la taille choisie reflète bien la quantité d’informations contenue dans les données.
Soit \(\mathscr{D}_n\) l’ensemble des données de taille \(n\).
On choisit en général une seule opération fondamentale13 ; pour \(d \in \mathscr{D}_n\), le coût \(c_A(d)\) d’une invocation \(A(d)\) par le programme \(A\) est le nombre d’opérations fondamentales qu’elle provoque. Le calcul exact de \(c_A(d)\) est rarement possible ; on s’intéresse alors plutôt à : \[\max_A(n)=\max\{c_A(d) \mid d \in \mathscr{D}_n\},\] complexité dans le pire des cas sur les données de taille \(n\) ou même à un simple majorant.
Prenons le programme [Prog1] en version «tant que» ; la donnée est un couple d’entiers \((a,\,b)\) ; comment en définir une taille ? On peut prendre \(a\), \(b\), \(a+b\), la somme des bits de l’écriture binaire de \(a\) et \(b\)… Le choix se fait en analysant le programme : clairement \(b\) ne compte pas. En revanche, \(a\) détermine le nombre d’itérations de la boucle «tant que» ; on prend donc \(a\) comme taille de la donnée \((a,\,b)\) ; puis les choses sont simples : par itération, on a une évaluation de booléen, un calcul de flottants (un produit et une somme), un appel de fonction de la bibliothèque math, un appel de la procédure pixel, deux affectations et pour terminer une évaluation de booléen. Aux fins de comparaisons de programme, compter le nombre d’appels de la procédure pixel n’est pas pertinent, car tout programme avec la donnée \((a,\,b)\) (\(b \leqslant a\)) affichera (au moins) \(a+1\) pixels. Par ailleurs, en Python, les opérations simples ont des temps d’exécution dans une fourchette disons de \(1\) à \(5\) (de l’ordre du dixième de micro-seconde, cela dépend bien sûr du matériel). On peut donc par exemple prendre l’appel de floor comme opération fondamentale. La complexité est alors exactement \(a\). On dit qu’elle est linéaire (sous-entendu «en \(a\)»).
Un test de mesure de durée confirme le résultat…
Passons maintenant au tracé des cercles.
Un cercle avec des flottants
La procédure d’affichage d’un pixel par une interface graphique accepte le plus souvent des arguments réels flottants (sans que le choix du pixel allumé soit bien documenté) ; cela permet d’écrire à volonté des programmes très simples. On considère donc pour l’instant que travailler avec des flottants n’est pas coûteux14.
Algorithme trigonométrique
Le cercle idéal de centre \((0,\,0)\) et de rayon \(r \in \mathbb{R}^+\) est représentable paramétriquement par les équations
\(x=r\cos(t),\,y=r\sin(t),\,t\in [0,\,2\pi[\)
En choisissant un nombre \(n\) de points à afficher (si \(R \geqslant 1\) est la mesure en pixels du rayon \(r\), \(n=\left\lceil \dfrac{\pi R}{4} \right\rceil\) est raisonnable pour les points d’un octant), on pose \(\delta = \dfrac{\pi}{4n}\) et on affiche les \(\big(R\cos(k\delta),\,R\sin(k\delta)\big)\), pour \(k\in[\![0,\,n ]\!]\) ; on complète par symétries. On vérifie que \(\delta \underset{R \to \infty}{\sim}\dfrac{1}{R}\cdotp\)
Cet algorithme est très simple à programmer sur tout matériel. Il est facile à adapter pour tracer un arc. Le principal inconvénient est l’utilisation de flottants et surtout les appels systématiques à des fonctions trigonométriques : trois produits de flottants, deux lignes trigonométriques par étape.
Une transformation
En posant \((x_i,\,y_i)=\left(\cos(i\delta),\,\sin(i\delta)\right)\), on cherche une relation de récurrence entre \((x_{i+1},\,y_{i+1})\) et \((x_i,\,y_i)\) ; un petit calcul conduit à :
\((x_{i+1},\,y_{i+1})=(x_i\cos(\delta)-y_i\sin(\delta),\,x_i\sin(\delta)+y_i\cos(\delta))\)
dans laquelle on reconnaît éventuellement l’expression analytique de la rotation de centre \((0,\,0)\) et d’angle \(\delta\) ; on voit le gain : deux lignes trigonométriques à calculer une seule fois, mais quatre produits de flottants à chaque étape. En initialisant à \((x_0,\,y_0)=(R,\,0)\), on a bien \(x_i^2+y_i^2=R^2\).
On peut songer puisque \(\delta\) est petit, à approcher \(\sin(\delta)\) par \(\delta\) et \(\cos(\delta)\) par \(1\). On a alors :
\((x_{i+1},\,y_{i+1})=\big(x_i-\delta y_i,\,\delta x_i + y_i\big)\)
On reconnaît cette fois une similitude directe, de rapport \(\sqrt{1+\delta^2}\) ; un calcul direct simple donne bien \(x_{i+1}^2+y_{i+1}^2=(1+\delta^2)(x_i^2+y_i^2)\) ; les \((x_i,\,y_i)\) ne sont donc pas à distance constante de \((0,\,0)\) et s’en éloignent progressivement.

Figure 2. R = 80 px, n = 63, zoom ×4.↩
Comme \(\delta \sim \dfrac{1}{R}\), un calcul assez classique donne \(\sqrt{x_{8n}^2+y_{8n}^2}-R \sim \pi\), soit \(3\) pixels sur un tour complet.
On perçoit (figure 2) d’autres inconvénients de ce cercle discret : il y a parfois des trous, souvent des pixels en trop (des coins).
Une erreur bénéfique
En voulant programmer le calcul du couple \((x’ ,\,y’ )=(x-\delta y,\,\delta x+y)\) en réutilisant les variables \(x\) et \(y\), une bourde classique est de produire le code
x=x-d*y |
bourde puisque, à la ligne 2, la valeur de x utilisée est celle redéfinie à la ligne 1. Or, si on programme le tracé du cercle avec ce code erroné, le résultat est étonnant15.

Figure 3. R = 40 px, n = 32, zoom ×8.
Ce calcul correspond à la relation de récurrence
\((x_{i+1},\,y_{i+1})=\big(x_i-\delta y_i,\,\delta x_i+(1-\delta^2)y_i\big)\)
relation affine de déterminant \(1\).
En posant \(\delta=2\sin(\varepsilon)\), les valeurs propres complexes de la matrice \(A=\begin{pmatrix} 1 &-\delta \\ \delta & 1-\delta^2 \end{pmatrix}\) sont \(\mathrm{e}^{-2\,\text{i}\,\varepsilon}\) et \(\mathrm{e}^{2\,\text{i}\,\varepsilon}\) ; on démontre alors classiquement (voir annexe) que \(A\) est semblable dans \(\mathfrak{M}_2(\mathbb{R})\) à la matrice \(\begin{pmatrix} \cos(2\varepsilon) & -\sin(2\varepsilon) \\
\sin(2\varepsilon) & \cos(2\varepsilon) \end{pmatrix}\) (semblable mais pas orthogonalement semblable). C’est ce qu’on appelle une rotation elliptique.
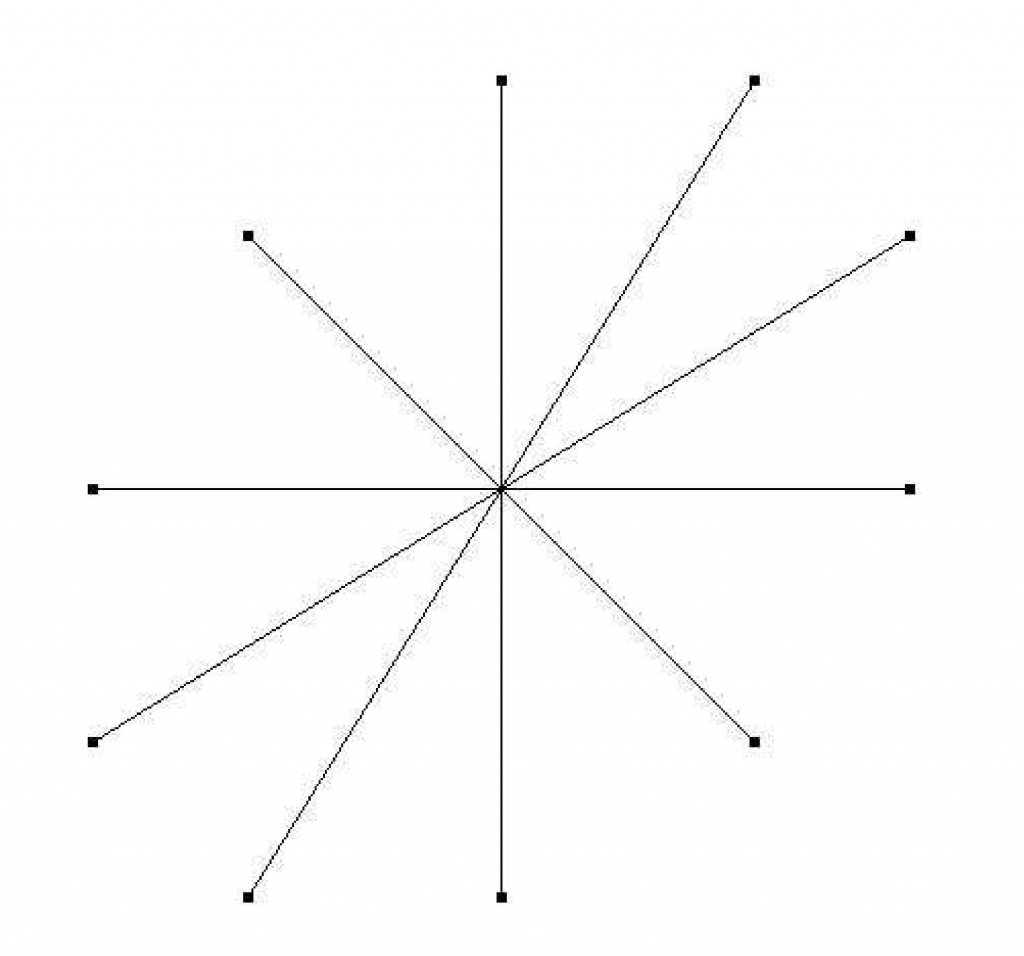
Figure 4. Rotation elliptique.↩
La figure 4 illustre le fonctionnement de l’itération d’une telle rotation avec \(\varepsilon=\dfrac{\pi}{10}\cdotp\) C’est exactement la perspective d’une rotation euclidienne.
Sans entrer dans les détails, on vérifie que
\(x_i^2-\delta x_iy_i+y_i^2=R^2\) ;
les \((x_i,\,y_i)\) sont donc sur l’ellipse d’équation
\(x^2-\delta xy+y^2=R^2\)
dont les axes de symétrie sont évidemment les droites \(y=x\) et \(y=-x\), d’où les demi-axes \(a=\dfrac{R}{\sqrt{\strut 1-\dfrac{\delta}{2}}}\) et \(b=\dfrac{R}{\sqrt{\strut 1+\dfrac{\delta}{2}}}\) et l’excentricité \(e\approx \sqrt{\delta}\). L’écart maximal (en pixels) au cercle idéal est \(R\left(\dfrac{1}{\sqrt{1-\delta/2}}-1\right)\sim\dfrac{1}{4}\) donc imperceptible.
Un cercle avec des entiers
Algorithme finlandais (1972)
Les auteurs proposent la fabrication d’une unité matérielle de calcul dédiée à l’affichage de cercles de mire sur un écran de télévision de 625 lignes à balayage entrelacé, c’est à dire qui affiche les lignes impaires puis les lignes paires. On va laisser de côté cette question d’entrelacement qui ne modifie pas de façon essentielle l’algorithme proposé. On oublie aussi les éventuelles questions de facteur d’aspect.
Sur le diamètre vertical d’un cercle de rayon \(R\), il y a \(2R+1\) lignes horizontales et sur chaque ligne, deux points du cercle (confondus aux sommets). Dans un repère où ces lignes ont une ordonnée \(k\) variant de \(1\) à \(2R+1\) et le centre du cercle est \((a,\,R+1)\), les luminophores du cercle ont pour abscisse
\(a \pm \sqrt{R^2-(k-(R+1))^2}\).
L’algorithme va consister à calculer le polynôme à valeurs entières \(X_k=R^2-(k-(R+1))^2\) par différences successives puis à calculer \(x_k=\left\lfloor \sqrt[]{X_k} \right\rfloor\) ou, mieux, \(x_k=\left[\strut\sqrt[]{X_k}\right]\), le calcul devant se faire assez vite pour permettre l’affichage en \(24\) images par seconde.
\[\begin{aligned}
\text{Posons }\Delta X_k&=X_{k+1}-X_k= 2R+1-2k\\
\text{et }\Delta^2 X_k&=\Delta X_{k+1}-\Delta X_k=-2\\
\text{avec }X_1&=0\text{ et }\Delta X_1=2R-1.\end{aligned}\]
Le calcul de la partie entière de la racine carrée en ne faisant que des additions est un grand classique de l’algorithmique.
Soit \(x \in \mathbb{R}^+\) et \(y=\left\lfloor \sqrt{x} \right\rfloor\). On a
\(y=\max\{h \in\mathbb{N} \mid h^2 \leqslant x\}\)
qui équivaut à \(y^2 \leqslant x < (y+1)^2\) ce qui permet d’introduire l’opérateur de minimisation :
\(y=\min\{h \in \mathbb{N} \mid h^2>x\}-1\)
le calcul de \(a_h=h^2\) se fait par différences successives : \(b_h=a_{h+1}-a_h=2h+1\) et \(b_{h+1}-b_h=2\).
L’algorithme est alors :
\(b_0=1\), \(a_0=0\)
\(b_n=b_{n-1}+2\), \(a_n=a_{n-1}+b_{n-1}\) pour \(n \geqslant 1\)
\(y=\min\{h \mid a_h >x\}-1\)
La programmation du \(\min{}\) se fait avec une boucle «tant que» qui nécessite le calcul itératif de \(h\) :
\(h_0=0 \textrm{ et } h_n=h_{n-1}+1\)
Le passage aux variables informatiques par élimination des récurrences et bonne gestion de l’ordre des affectations conduit au programme :
| Fonction perac |
def perac(x):"""renvoie la partie entière de la racine carrée de x>=0"""#INITIALISATIONh=h+1return(h-1)
|
On pourrait simplifier un soupçon en remplaçant h par h+1. Le lecteur pourra vérifier que \(b=2h+1\) et \(a=h^2+1\) sont des invariants de la fonction perac fournis ici encore par l’algorithme.
Intéressons-nous à la complexité de la fonction perac. On prend comme taille de la donnée x, x lui-même ; comme opération fondamentale l’évaluation du booléen not(a> ;x). L’entier h est un compteur d’exécution de la boucle, le nombre d’opération fondamentale est donc la valeur finale de h, soit \(\left\lfloor \sqrt{\texttt{x}} \right\rfloor+1\). La complexité est sous-linéaire ; une expérimentation basique permet de vérifier qu’une multiplication par \(4\) de \(x\) provoque bien un doublement du temps de calcul.
On peut alors écrire le programme d’allumage des luminophores (en prenant \(a=0\)) en se contentant du premier quart de cercle (programme 4).
On voit sur la figure 5 (cercle complet) le principal défaut : la non-connexité (par arc), mais qui n’est pas gênante sur un écran TV à balayage.
| Fonction cercle_lappa |
def cerclelappa(R) :X,DX=0,2*R-1x=perac(X) |
L’algorithme de calcul de \(\left[\sqrt{x}\right]\) est laissé à la sagacité du lecteur…
Intéressons-nous à la complexité du programme cercle_lappa. En prenant le rayon \(R\) (en pixels) comme taille de la donnée, et comme opération fondamentale l’appel de perac, on a une complexité en temps égale à \(\displaystyle\sum_{k=1}^{R+1}\left(\left\lfloor \strut \sqrt{X_k} \right\rfloor+1\right)\) somme dans laquelle on reconnaît (par construction !) une approximation en px\(^2\) de l’aire du quart de cercle. Donc \[\sum_{k=1}^{R+1}\left(\left\lfloor \strut \sqrt{X_k} \right\rfloor+1\right) \underset{R\to+\infty}{\sim}\ \frac{\pi}{4}R^2\]
la complexité est dite quadratique.
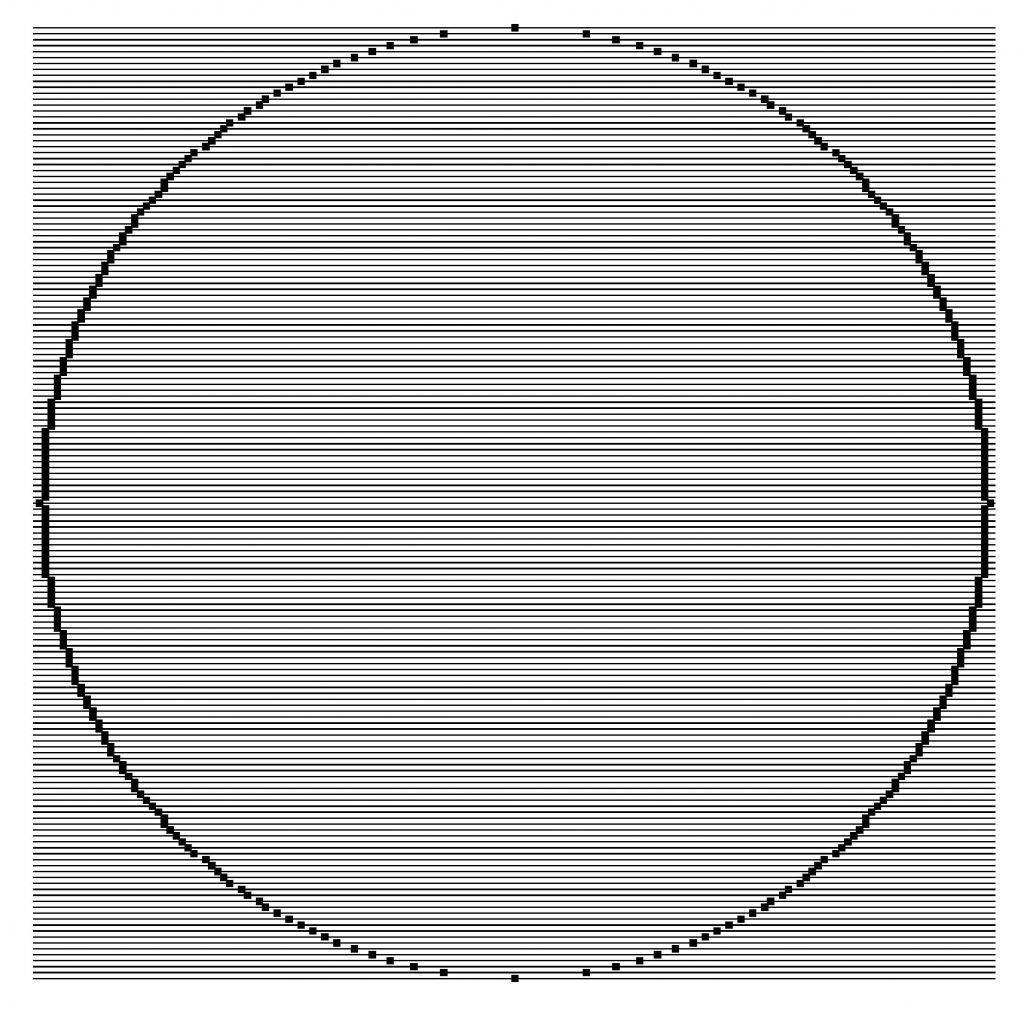
Figure 5. Cercle L. et O., R = 80 px.↩
On peut améliorer cette complexité de diverses façons ; d’abord, l’appel de perac comme fonction externe est coûteux puisque le calcul itératif redémarre à \(0\) alors qu’on pourrait partir de la valeur précédemment trouvée ; ce sera fait dans le programme .
Ensuite, il est possible de transformer le programme perac en un programme n’utilisant toujours que des additions d’entiers, des multiplications par \(2\) et des divisions entières par \(2\) pour obtenir une complexité logarithmique, c’est-à-dire en \(\log_2(x)\), ce qui fournit une complexité pour cercle_lappa en \(R\log_2(R)\). Le développement de tout cela est hors de propos ici.
Algorithme de Michener
Michener16 améliore un algorithme incrémental antérieur de Bresenham (1965) fondé sur la fonction de décision \(\Delta(x,\,y)=x^2+y^2-r^2\).
On va en donner une construction «à la mode programmeur», c’est-à-dire en raisonnant directement sur les valeurs des variables du programme.
On souhaite tracer le premier octant du cercle \(x^2+y^2=r^2\) (\(r\geqslant 1\)). Pour \(j\) fixé dans \(\left[\!\!\left[0,\,\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\right]\!\!\right]\), on cherche \(i\) minimisant \(\rule{0pt}{12pt}|\Delta(i,\,j)|=|i^2+j^2-r^2|\). On verra dans la section que cela équivaut à minimiser \(\left|i-\sqrt{\strut r^2-j^2}\right|\) ; la solution est donc \[i=\left[\sqrt{\strut r^2-j^2}\right].\] Comme dans l’algorithme de Bresenham pour les segments, on cherche un algorithme incrémental pour calculer \(i\) : le pixel \((i,\,j)\) étant allumé, quel est le suivant \((i’ ;,\,j’ ;)\) avec \(j’ ;=j+1\) ? Une étude de la fonction \(\varphi\colon j \longmapsto \left[\sqrt{\strut r^2-j^2}\right]\) fournit sa décroissance avec des sauts d’au plus \(1\), c’est-à-dire que \(i’ ;= i\) ou \(i-1\) (on donnera une démonstration géométrique de ceci dans la section ).
Pour choisir entre ces deux cas, on compare \(|\Delta(i,\,j+1)|\) et \(|\Delta(i-1,\,j+1)|\) ; comme
\(\Delta(i,\,j+1)-\Delta(i-1,\,j+1)=2i-1>0\),
il suffit de tester le signe de \[d=\Delta(i,\,j+1)+\Delta(i-1,\,j+1).\] Si \(d \leqslant 0\) alors \(i’ ;=i\) et \(j’ ;=j+1\) ; sinon \(i’ ;=i-1\) et \(j=j+1\).
Le calcul de \(d\) peut se faire de façon incrémentielle ;
-
si \(d \leqslant 0\) alors \(i’ ;=i\) et \(j’ ;=j+1\) donc
\(d’ ;=\cdots= d+(4j+6)\) ;
-
si \(d>0\) alors \(i’ ;=i-1\) et \(j’ ;=j+1\) donc
\(d’ ;=\cdots= d +4(j-i)+10\).
Récapitulons ; on a trois variables : \(i\), \(j\), \(d\) dont l’initialisation est \(i=r\), \(j=0\), \(d=3-2r\). Le triplet \((i,\,j,\,d)\) étant connu, on sait déterminer \((i’ ;,\,j’ ;,\,d’ ;)\) donc mettre à jour les variables \(i,\,j,\,d\). Reste le critère d’arrêt : lorsqu’on sort du premier octant, soit \(j > i\). On peut écrire un premier programme (programme 5).
Il est d’usage de considérer que le travail préalable à l’écriture de ce programme le valide, au même titre que le ferait un travail sur les suites indicées.
| Fonction Michener |
def Michener(r) :i,j,d = r,0,3-2*rpixel(i,j)d = d+4*j+6 else:d = d+4*(j-i)+10j = j+1 return(None)
|
Pour le lecteur qui voudrait s’exercer à une preuve sur le modèle de celle du programme [Prog1], le travail effectué fournit l’invariant principal :
\(d=i^2+(i-1)^2+2(j+1)^2-2r^2\)
Variant et terminaison sont évidents. La spécification du programme est
-
Précondition : \(r \geqslant 1\) ;
-
Postcondition : pour tout \(j \in\left[\!\!\left[0,\, \left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\right]\!\!\right]\), le pixel \(\left(\left[\sqrt{\strut r^2-j^2}\right],\,j\right)\) est allumé.

Figure 6. Cercles de Michener
\(R=1\), \(4\), \(8\), \(11\), \(16\), \(23\), \(37\), \(52\) px, zoom \(\times 8\).
Le programme Michener peut être amélioré en utilisant des différences secondes pour le calcul de \(d\)…
Algorithme de Horn (1976)
Travaillons par transformation de programme ; on part d’un programme simple de tracé de graphe de fonction pour le premier octant du cercle idéal \(x^2+y^2=r^2\), \(r \geqslant 1\) ; le principe est le suivant : pour chaque intersection du cercle idéal avec une ligne horizontale, on choisit le point du réseau sur cette horizontale le plus proche de l’intersection. Il est utile d’observer qu’il n’y a jamais ambiguïté car le cercle idéal ne peut passer par un point dont l’abscisse est demi-entière et l’ordonnée entière.
x,y = r,0pixel(x,y) |
Il s’agit de se débarrasser de la ligne 5 en la remplaçant par une mise à jour sous condition de la variable \(x\).
Or, en utilisant la définition de la partie entière, on a \(x=\left\lfloor \sqrt{\strut r^2-y^2}+\dfrac{1}{2} \right\rfloor=\varphi(y)\) si et seulement si \(x \in \mathbb{N}\) et \(\left(x-\dfrac{1}{2}\right)^2+y^2<r^2<\left(x+\dfrac{1}{2}\right)^2+y^2\) (inégalité stricte à gauche pour le motif de non-ambiguïté évoqué ci-dessus).
Posons \(\Delta(x,\,y)=(x-\dfrac{1}{2})^2+y^2-r^2\), \(y’ ;=y+1\) et \(x’ ;=\varphi(y’ ;)\).
On a \(x’ ;=x\) si et seulement si
\(\Delta(x,\,y+1)<0<\Delta(x+1,\,y+1)\)
L’inégalité de droite est vérifiée puisque
\(0<\Delta(x+1,\,y)<\Delta(x+1,\,y+1)\)
On aura donc \(x’ ;=x-1\) si et seulement si \(\Delta(x,\,y+1)>0\). D’où le programme
x,y = r,0pixel(x,y)x=x-1 |
Il reste à calculer \(\Delta(x,\,y)\) de façon incrémentielle : on a \(\Delta(x,\,y+1)=\Delta(x,\,y)+2y+1\) et \(\Delta(x-1,\,y)=\Delta(x,\,y)-2x+2\), et \(\Delta(r,\,0)=-r+\dfrac{1}{4}\cdotp\)
x,y,d=r,0,-r+0.25pixel(x,y)d=d-2*x+2 |
Pour obtenir un algorithme sur entiers uniquement, il suffit de remplacer la variable \(d\) par \(4d\) ce qui ne change pas son signe. Horn observe qu’il suffit de remplacer \(d\) par \(d-\dfrac{1}{4}\) en modifiant l’initialisation ; il convient alors de changer le test \(d>0\) de mise à jour de \(x\) en \(d \geqslant 0\). En prenant garde à la place des mises à jour de \(d\), on obtient le programme final (programme 6).
On perçoit (figure 7) une particularité de certains cercles discrets qui possèdent un coin sortant sur la diagonale : \(R=4\), \(R=11\) particularité déjà présente dans les cercles de Michener. Les valeurs de \(r\) pour lesquelles un tel coin apparaît peuvent être déterminées.
| Fonction Horn |
x,y,d=r,0,-rpixel(x,y)x=x-1 |
La détermination de la complexité pose aussi un problème intéressant ; en prenant toujours comme taille de la donnée la mesure \(R\) en pixels du rayon \(r\) et en prenant comme opération fondamentale soit les tests, soit les additions, soit les multiplications par 2, on voit que le nombre de telles opérations est fonction du nombre de validations du test \(d \geqslant 0\).

Figure 7. Cercles de Horn
R = 1, 4, 8, 11, 16, 23, 37, 52 px, zoom ×8. ↩
Or ce nombre peut être estimé17 ; la dernière exécution de la boucle tant que a lieu lorsque \(y = x\) qui sont alors voisins de \(\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\) ; pour passer de la valeur initiale \(r\) à cette valeur, \(x\) est décrémentée \(r-\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\) fois ; la boucle tant que est exécutée environ \(\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\) fois. La complexité, mesurée par exemple en additions, est donc, à quelques unités près,
\(3\left(\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\right)+2\left(r-\left\lfloor \dfrac{r}{\sqrt{2}} \right\rfloor\right) \approx \left(2+\dfrac{1}{\sqrt{2}}\right)r\)
L’algorithme DCS (2008)
Imaginé par deux universitaires indiens, cet algorithme amusant met en relation cercles et carrés parfaits18.
Considérons le deuxième octant du cercle Bresenham-Michener de rayon \(41\) (figure 8) ; il est constitué de segments discrets horizontaux de longueur \(7\), \(4\), \(4\), \(2\), \(2\), \(2\), \(2\), \(1\), \(1\), \(2\), \(1\), \(1\), \(1\) appelés «runs». La connaissance de cette suite permet bien sûr le tracé du cercle.
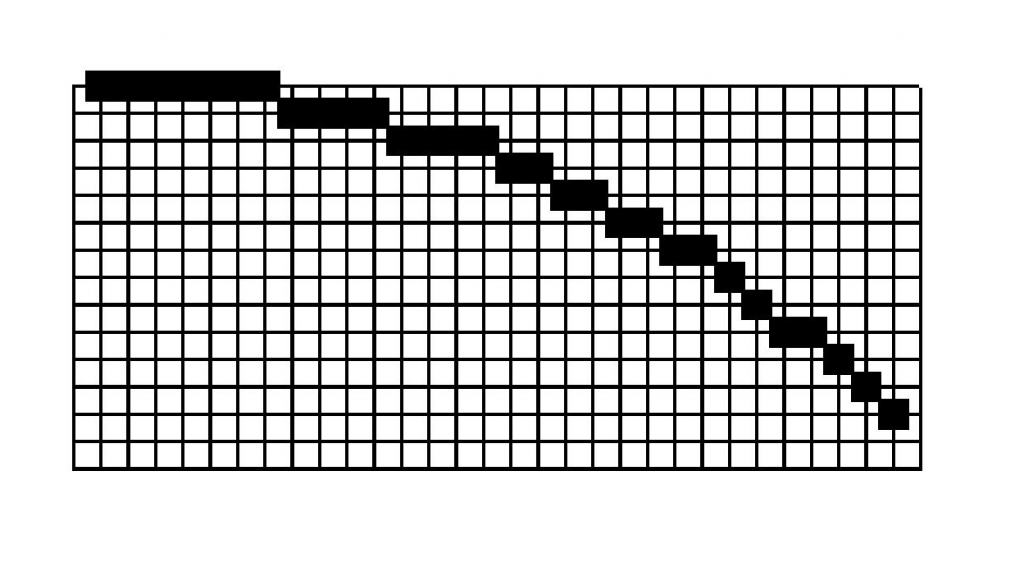
Figure 8. « runs » du cercle de Bresenham
R = 41 px, zoom ×8. ↩
La trouvaille de Bhowmick et Bhattacharya est la suivante : le premier «run» \(7\) est le nombre de carrés d’entier entre \(0\) et \(r-1=40\) ; en effet : \(\mathrm{card}(\{0,\,1,\,4,\,9,\,16,\,25,\,36\})=7\). De même, le second \(4\) est le nombre de carrés d’entier entre \(r=41\) et \(3r-3=120\), le troisième dénombre ceux entre \(3r-2=121\) et \(5r-7=198\) ; plus généralement, le \((k+1)\)-ième «run» est le nombre de carrés d’entier entre \(u_k=(2k-1)r-k(k-1)\) et \(v_k=(2k+1)r-k(k+1)-1=u_{k+1}-1\) (\(k \geqslant 1\)).
La démonstration de ceci est tout à fait simple ; le pixel \((i,\,j)\) est allumé si et seulement si \(j=\left\lfloor \sqrt{\strut r^2-i^2}+\dfrac{1}{2} \right\rfloor\) soit, en tenant compte de diverses observations faites antérieurement, si et seulement si \(r^2-j^2-j-\dfrac{1}{4} < i^2 < r^2-j^2+j-\dfrac{1}{4}\) ce qui, compte tenu du fait que \(i\), \(j\) et \(r\) sont entiers, équivaut à :
\[\tag{IF}\label{eqIF}
r^2-j^2-j \leqslant i^2 <r^2-j^2+j\]Toute l’habileté est alors de savoir lire l’information contenue dans ; prenons \(j=r\) (le premier «run») ; les \(i\) autorisés et admis (par condition nécessaire et suffisante) sont ceux vérifiant \(-r \leqslant i^2 < r\) soit \(0 \leqslant i^2 \leqslant r-1\). Avec \(j=r-k\), on retrouve les \(i\) vérifiant \(u_k \leqslant i^2 \leqslant v_k\).
Reste à transformer ces mathématiques en algorithme.
Posons \(u_0=0\), \(w_0=r\), et \[w_k=v_k-u_k+1=2r-2k\text{ pour }k \geqslant 1\, ;\] la suite \((w_k)\) est définie par \(w_0=r\), \(w_1=2r-2\), \(w_k=w_{k-1}-2\) et la suite \((v_k)\) par \(v_k=v_{k-1}+w_{k}\) pour \(k \geqslant 1\).
Les carrés se calculent comme dans le programme perac avec des additions (variables \(s\) et \(t\)). (programme 7). Programme remarquable, n’utilisant que des additions. «\(\ll\)» est l’opérateur de décalage des bits ; l’instruction 3 équivaut à w = 2*v.
| Fonction DCS |
def DSC(r):i,j,s,t,v = 0,r,0,1,r-1# boucle des carréspixel(i,j)v=v+wreturn(None) |
Il est très instructif pour ce programme à \(6\) variables de dresser un tableau de suivi de valeurs ; \(r=11\) est raisonnable. Pour mieux suivre le flot d’exécution, on ne réécrit pas les valeurs des variables non mises à jour.
\[\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
i & j & s & t & v & w & j \geqslant i & s \leqslant v &\textrm{pixel}\\ \hline
0 &11 &0 & 1 &10 & 20 &\mathsf{V} & \mathsf{V} &(0,11) \\ \hline
1 & & 1 &3 & && & \mathsf{V} & (1,11) \\ \hline
2 & & 4 & 5 && & & \mathsf{V} &(2,11) \\ \hline
3 && 9 &7 & & && \mathsf{V} & (3,11) \\ \hline
4 &&16& 9 && && \mathsf{F} & \\ \hline
&10 && & 30 & 18 & \mathsf{V} & \mathsf{V} & (4,10) \\ \hline
5 & & 25&11&& & & \mathsf{V} & (5,10) \\ \hline
6 & & 36& 13& && &\mathsf{F} & \\ \hline
& 9 & & & 48 & 16 & \mathsf{V} & \mathsf{V} & (6,9) \\ \hline
7 && 49& 15&& & & \mathsf{F} & \\ \hline
&8 & & & 64 & 14 & \mathsf{V} & \mathsf{V} & (7,8) \\ \hline
8 & & 64& 17&& & &\mathsf{V} & (8,8) \\ \hline
9 && 81& 19& & & \mathsf{F} &\\ \hline
& 7 & && 78 &12 & \mathsf{F} & & \\ \hline
\end{array}\]
Figure 9. Suivi d’exécution de DCS(11).
Un même cercle pour différents algorithmes
Un peu de vocabulaire pour commencer ; un élément de \(\mathbb{Z}^2\) sera appelé un point. On oublie les pixels… Une maille de \(\mathbb{Z}^2\) est un quadruplet de points sommets d’un carré de côté 1.
Une section d’un cercle idéal est le côté d’une maille coupé par le cercle en un point appelé point de section ; on peut distinguer les \(x\)-sections et les \(y\)-sections. Si le cercle passe par un sommet d’une maille, il y a quatre sections associées.
On va considérer parmi les discrétisés possibles d’un cercle idéal de rayon \(r\) ceux qui sont obtenus par l’un des trois procédés suivants :
-
chaque point du discrétisé est l’extrémité de la section la plus proche du point de section. (on va voir qu’il ne peut pas y avoir ambiguïté) ; on parlera de F-discrétisé19 ;
-
chaque point du discrétisé est l’extrémité de la section qui minimise \(|x^2+y^2-r^2|\) ; on parle de B-discrétisé20 ;
-
chaque point du discrétisé est l’extrémité de la section qui minimise \(\left|\sqrt{\strut x^2+y^2}-r\right|\) ; on parle de R-discrétisé21.
On suppose \(r\) entier plus grand que \(1\)22. Un simple argument de parité permet de prouver les trois propriétés suivantes :
-
\(\mathrm{B}(x,\,y)=\left|x^2+y^2-r^2\right|\) ne peut prendre la même valeur en deux points dont la distance est \(1\), en particulier aux extrémités d’une section.
-
\(\mathrm{R}(x,\,y)=\left|\sqrt{\strut x^2+y^2}-r\right|\) ne peut prendre la même valeur aux extrémités d’une section.
-
Le cercle idéal \(x^2+y^2-r^2=0\) ne peut passer par un point dont une coordonnée est demi-entière et l’autre entière.
Par exemple, la seconde : par l’absurde ; sinon il existerait, disons une \(x\)-section, telle que
\(0<r-\sqrt{\strut x^2+y^2} = \sqrt{\strut (x+1)^2+y^2}-r\)
\(\bigl((x,\,y)\) intérieur et \((x+1,\,y)\) extérieur\(\bigr)\) ; on aurait alors après quelques manipulations et élévations au carré :
\((4r^2+2x+1)^2=16r^2\left((x+1)^2+y^2\right)\) soit l’égalité d’un impair et d’un pair ; contradiction.
La première (resp. seconde) propriété montre qu’il y a unicité du cercle B-discrétisé (resp. R-discrétisé) puisqu’il y a, pour chaque section, un seul point possible. La troisième propriété prouve que le point de section ne peut pas être au milieu de la section ; donc il n’y a jamais ambiguïté pour un F-discrétisé.
On peut alors démontrer le théorème suivant (emprunté à [4]) :
| Théorème |
|
Les trois types de cercle discrétisé introduits précédemment coïncident. |
Commençons par l’identité du B-discrétisé et du R-discrétisé. Il s’agit de prouver que, si le cercle idéal a disons une \(x\)-section entre \((x,\,y)\) et \((x+1,\,y)\), alors les éléments des deux couples \(\left(\left|\sqrt{\strut x^2+y^2}-r\right|,\,\left|\sqrt{\strut (x+1)^2+y^2}-r\right|\right)\) et \(\left(\left| x^2+y^2-r^2\right|,\,\left|(x+1)^2+y^2-r^2\right|\right)\) sont dans le même ordre (nécessairement strict). Il y a beaucoup de cas à envisager ; supposons par exemple que
\[\tag{1}\label{bouchereq1}
r-\sqrt{\strut x^2+y^2}< \sqrt{\strut (x+1)^2+y^2}-r\]
et
\[\tag{2}\label{bouchereq2}
r^2-x^2-y^2<(x+1)^2+y^2-r^2\]
fournit
\(4r^2>2x^2+2y^2+2x+1+2\sqrt{\strut x^2+y^2}\sqrt{\strut (x+1)^2+y^2}\)
l’inégalité de Cauchy-Schwarz donne
\(\sqrt{\strut x^2+y^2}\sqrt{\strut (x+1)^2+y^2} \geqslant x(x+1)+y^2\) d’où l’on déduit, avec , \(x^2+y^2+x+\dfrac{1}{4} <r^2 < x^2+y^2+x+\dfrac{1}{2}\) incompatibles avec \(x\), \(y\) et \(r^2\) entiers.
La démonstration de ce premier point se complète aisément.
Ensuite, prouvons l’identité du R-discrétisé et du F-discrétisé ; l’argument est plutôt subtil : minimiser par exemple \(\left|x-\sqrt{\strut r^2-y^2}\right|\) à \(y\) fixé, revient à minimiser \(|x-s|\) où \(s^2=r^2-y^2\). Mais minimiser \(|x-s|\) est un F-problème avec l’axe des abscisses pour le cercle de rayon \(s\) avec \(s^2\) entier dont la solution coïncide donc avec celle du minimum de \(|x^2-s^2|=|x^2+y^2-r^2|\).
En conclusion
Notre promenade s’achève dans les années 1980 ; par la suite, les progrès technologiques aidant, la recherche va se déplacer vers des contrées plus abstraites. La géométrie discrète telle qu’initiée par Jean-Pierre Reveillès dans les années 1990 cherche à définir les objets discrets non pas comme objet produit par un algorithme mais par des propriétés de nature arithmétique, essentiellement des inéquations diophantiennes. On peut alors chercher à obtenir des objets possédant des propriétés permettant leur reconnaissance.
On trouvera dans l’article de Reveillès [5] des développements très accessibles sur ces questions.
Annexes↩
La procédure pixel
Le module turtle dispose de la fonction dot prenant en argument un entier \(n\) non nul et affichant (à la position de la tortue) un point dont la taille (et la forme) est déterminée par son argument ; à partir de \(n=5\), le point est d’allure circulaire de diamètre l’argument. Pour \(n=1\), le point est invisible ; pour \(n=2\), le point est exactement un pixel, pour \(n=3\), une croix (\(+\)) \(3\) px sur \(3\) px, et pour \(n=4\), un carré (\(\blacksquare\)) \(3\) px sur \(3\) px.
| Fonction pixel_1 |
from turtle import*up() # lève la plume |
Cette fonction suffit pour le rendu final mais ne permet pas de voir les pixels se dessiner.
On peut simuler un zoom (pair) \(\times n\), par défaut à \(4\), en plaçant le centre des pixels aux points du réseau.
| Fonction pixel_2 |
from turtle import*color(’black’)# ensuitefor i in range (4):forward(n) # avance de n dans la# direction de la tortue left(90) # tourne à gauche de 90°end_fill() |
Mesure de complexité temporelle
Le principe, un peu naïf, est de mesurer la durée d’exécution d’un programme — avec un chronomètre — en faisant varier la taille de la donnée de façon à obtenir un jeu de valeurs permettant d’évaluer expérimentalement la complexité temporelle (ou de confirmer un calcul théorique).
Le principe est qualifié de naïf car un ordinateur fait en permanence bien d’autres choses que d’effectuer les opérations des lignes de code testées et on ne sait pas trop ce que l’on mesure. On peut penser qu’en répétant un grand nombre de fois la mesure et en prenant le minimum des durées, on obtient une mesure plus significative.
Le mieux est de ne pas oublier que «Python est livré avec les piles» et d’utiliser l’outil conçu pour cela : .
Un exemple minimal23 en ligne de commande dans une fenêtre IDLE devrait suffire :
<>>>from timeit import timeit... >>>L=[4**n for n in range(5,15)]timeit(“perac(n)”,number=1000, |
En ligne 1, on importe la fonction timeit, ligne 2-3 on définit la fonction perac, ligne 4, on construit la liste des arguments réels qui vont être testés, et ligne 5-8, on exécute la fonction timeit avec trois arguments : le premier est une chaîne contenant le code qui va être testé, le second est le nombre de répétitions de l’exécution du code ( par défaut) et le troisième permet à timeit d’utiliser les fonctions dont le nom est dans l’espace de nom globals() ici perac.
L’exécution fournit les résultats suivants :
|
0.012283500248884138
0.0237704164145498 0.04335659532540603 0.09550758945681537 0.22917897760129335 0.5025265294473229 1.0326946844788836 2.1086930692052874 4.275860462784522 8.569076826942705 |
Les nombres obtenus correspondent au temps d’exécution en seconde de appels de perac(n) ; ce qui confirme que multiplier l’argument par \(4\) double le temps d’exécution.
Un théorème d’algèbre linéaire
Soit \(A\) une matrice \(2\times 2\) à coefficients réels admettant \(\lambda_{\pm}=a\pm \text{i}\,b\) (\(b \neq 0\)) comme valeurs propres complexes (non réelles) et \(V_{\pm}=\begin{pmatrix} p\pm \text{i}\,q \\ r \pm \text{i}\,s \end{pmatrix}\) les colonnes propres complexes associées. En posant \(U=\begin{pmatrix} p & q \\ r & s \end{pmatrix}\), on a \(U^{-1}A U=A’ ;=\begin{pmatrix} a & b \\ -b & a \end{pmatrix}\).
On peut vérifier par force brute que \(AU=UA’ ;\)… Un calcul sur les colonnes utilisant \(AV_+=\lambda_+V_+\) et la très utile \(C_k(AB)=AC_k(B)\) est plus élégant. Enfin \(U\) est inversible car ses lignes sont \(\mathbb{R}\)-indépendantes puisque les vecteurs propres \(V_+\) et \(V_{-}\) le sont.
Un grand merci à François Bouyer et à Vincent Beck pour leurs relectures des plus attentives.
Références
- Barrera, Hast et Bengtsson. « A chronological and mathematical overview of digital circle generation algorithms. » In : International Journal of Computer Mathematics (2015). ↩
- Patrick Bosc, Marc Guyomard et Laurent Millet. Conception d’algorithmes. Eyrolles, 2016. ↩
- Gilles Dowek et alii. Introduction à la science informatique. Paris : C.R.D.P., 2011. ↩
- Douglas McIlroy. « Best approximate circles on integer grids ». In : ACM Transactions on Graphics (1983). ↩
- Jean-Pierre Reveillés. « Géométrie et ordinateurs, droites, cercles, paraboles ». In : Gazette SMF (1998). ↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
François Boucher est tout jeune retraité de l’Éducation Nationale. Il a enseigné les mathématiques et l’informatique en CPGE au lycée Bellevue à Toulouse.
-
Voir [1] pour une synthèse partielle assez bien documentée.↩
-
Attribuées à Kenneth Eugène Iverson (1920-2004), informaticien canadien, concepteur du langage APL.↩
-
Choix arbitraire ; on pourrait convenir de choisir le plus petit.↩
-
Les modernes disent rastérizée… pchittt !↩
-
Jack Bresenham (1937– ) : informaticien qui a fait une bonne partie de sa carrière chez IBM. Ses travaux ici évoqués datent des années 1960.↩
-
Un commentaire est fait après le programme suivant sur
pixelet lereturn(None)terminal.↩ -
Le tuple est un type de données qu’on peut voir dans une certaine mesure comme l’image informatique du \(n\)-uplet mathématique.↩
-
Il s’agit bien de l’égalité de valeur des variables, donc d’un prédicat ; en contexte Python, on pourrait utiliser \(i == a\).↩
-
Bien entendu, ces invariants ne tombent pas du ciel, mais sont des sous-produits de l’algorithme précédemment décrit !↩
-
Ceci peut faire l’objet d’une démonstration, mais en informatique comme en mathématique, on ne démontre pas les évidences…↩
-
On disait aussi «évaluation» ; les modernes disent «complexité» ; ce dernier terme s’est imposé.↩
-
Il y a là une ambiguïté difficile : complexité algorithme/complexité programme qu’on va prudemment taire ici.↩
-
Il est loisible d’en prendre plusieurs. Mais si ces opérations fondamentales ont des durées d’exécution constantes, seule celle qui est exécutée le plus souvent déterminera le coût temporel asymptotique final.↩
-
Les cartes graphiques pour «gamer» ont une puissance de calcul qui dépasse les \(10\) teraflops et une capacité d’affichage qui atteint \(140\) gigapixels par seconde ; pourquoi diable se fatiguer ?↩
-
Qui a bien pu avoir cette idée ? Peut-être Yvan Sutherland (1938– ), pionner de l’informatique graphique, auteur entre autres choses, du système Sketchpad. Dans sa thèse (1963), il signale l’intérêt de ce code pour tracer efficacement des cercles, mais ne l’utilise pas car il ne permet pas le calcul parallèle. En revanche, il l’utilise pour calculer les lignes trigonométriques ; merci à Jack Volder et à son algorithme CORDIC (1956).↩
-
Il ne semble pas possible de trouver la moindre information sur Jim Michener ; tout le monde ou presque appelle algorithme de Bresenham ce qui devrait être appelé algorithme de Michener.↩
-
Un calcul exact semble un problème non trivial.↩
-
Partha Bhowmick et Bhargab Bhattacharya ; DCS=digital circle square.↩
-
«F» comme Freeman Herbert (1925– ) informaticien américain d’origine allemande.↩
-
«B» comme Bresenham.↩
-
«R» comme radial.↩
-
Le lecteur volontaire pourra vérifier que tout ce qui suit reste valide si \(r^2\) seulement est entier.↩
-
Bien sûr, rien ne remplace la consultation de la documentation pour prendre connaissance des possibilités offertes par le module.↩
