Jeux de boules

On appelle nombres figurés les nombres entiers qui peuvent être représentés par un ensemble de points disposés régulièrement suivant une figure géométrique.
Henry Plane présente ici quelques résultats concernant ces nombres, en considérant le cas particulier, cher aux artilleurs, des assemblages de sphères.

Henry Plane

© APMEP Décembre 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Existe-t-il un passé, fût-il lointain, où assembler les boules en triangle, en carré, en hexagone… a été d’un grand intérêt ? On pourrait le penser en constatant combien le dénombrement des éléments constituant ces assemblages — les nombres polygonaux — a laissé de traces même s’il dépasse rapidement le problème concret évoqué car assembler des boules en heptagone ! … Certes on peut penser qu’il s’agissait alors de planter des piquets, voire des arbres, pourquoi pas des quinconces orthogonaux ? … Donc ces nombres, les nombres polygonaux, prennent place dans les anciens traités d’arithmétique avec les moyens de les calculer de proche en proche, itérations amorces de récurrences. Il ne pouvait guère être question d’expression générale tant que Viète n’avait pas fourni le moyen de l’écrire. Peut-être pour le cas des carrés, nombre tétragonal, pouvait-on risquer une formulation mais pour les autres ce n’était, au mieux, qu’exemples numériques de suites régulièrement rythmées se généralisant.

Dans l’Institutio arithmetica de Boèce au livre 2 — chapitres 9 à 19 —, on trouve à peu près le texte suivant — nous sommes au début du  siècle ; il écrit en latin¹ :

Pour engendrer le nombre triangulaire nous ajoutons les nombres de la série naturelle qui se suivent d’une unité.

Pour les nombres tétragonaux on a joint la suite des nombres qui se dépassent de deux en deux à partir de un.

Pour les pentagonaux on ajoute ceux qui se suivent de trois en trois à partir de un.

Alors pour les hexagonaux, les heptagonaux, les octogonaux et les autres ce sera des accroissements de même nature à partir de un, de quatre en quatre, de cinq en cinq…

Boèce donne une table. Celle reproduite ici figure dans la première impression de l’arithmétique de Boèce (Venise, 1499).

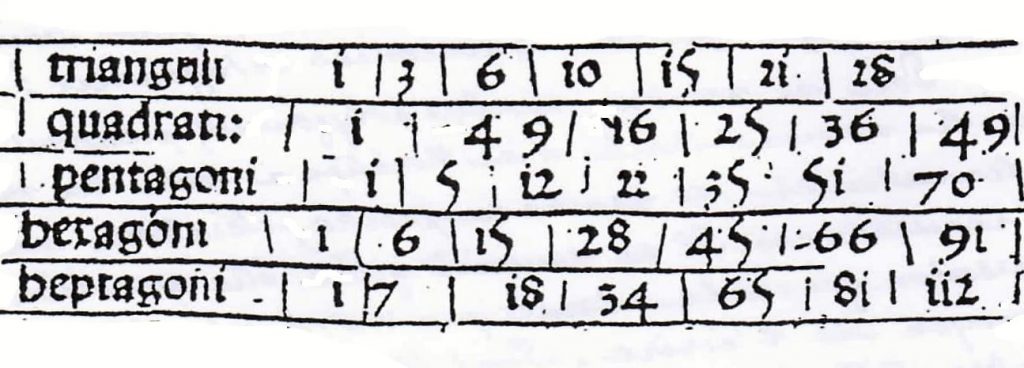
Mais il est bon de noter que le sens du problème s’était perdu au cours du Moyen-Âge, si ce n’est antérieurement, pour ne garder que celui d’un calcul rythmé. On s’en apercevra avec la figure qui accompagne le tableau précédent dans l’incunable vénitien.

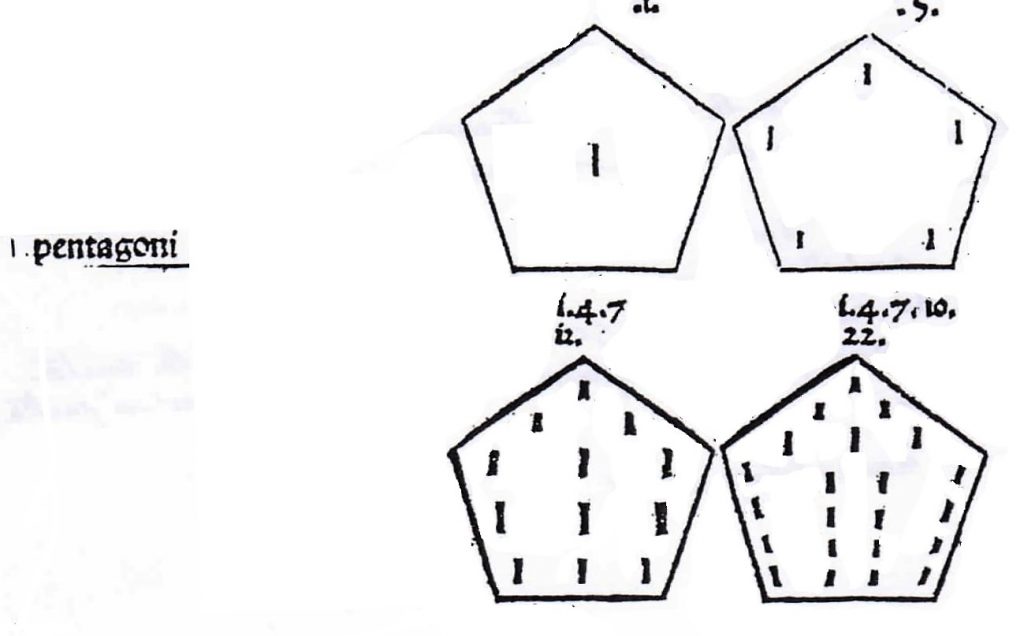
Ces dénombrements restent encore sujets d’étude au  siècle. Euler (1707–1783), grand amateur de calculs, donne la démonstration de l’expression du nombre de rang \(n\) correspondant au polygone d’ordre \(q\) : \[P_n^q=\dfrac{(q-2)n^2-(q-4)n}{2}\] Ainsi pour les nombres triangulaires : \(P_n^3=\dfrac{n^2+n}{2}\cdotp\)

Dans les ouvrages de mathématiques de ce  siècle, et plus particulièrement ceux des écoles militaires, on s’intéresse en outre à l’entassement des boules. Boèce en parlait déjà (Livre 2 chapitres 20 et suivants : les nombres solides, pyramides à bases triangulaire ou tétragonale) et il énonçait quelques résultats.

Mais pourquoi cet intérêt entretenu en la circonstance ? Parce que les boules pouvaient être des boulets !

Il s’agissait d’évaluer rapidement les réserves en boulets dans les forteresses où ceux-ci étaient entassés. À la vue du tas et d’une simple évaluation d’une arête, il s’agissait de connaître la réserve en munitions.

Pyramide à base triangulaire (tétraèdre…)

Sur le triangle de trois boulets, on peut en monter un et placer le tout dans les intervalles d’un autre triangle de trois boulets de côté.

Si on dénombre \(1+3+6+\cdots+\dfrac{n(n+1)}{2}\), en continuant : \(T_n=P_1^3+P_2^3+P_3^3+\cdots+P_n^3\), l’étude précédente reprend tout son sens.

\[T_n=\sum_{i=1}^n \dfrac{i^2+i}{2}=\dfrac{1}{2} \left(\sum_{i=1}^n i^2+\sum_{i=1}^n i\right)\]

Il faut calculer la somme des carrés des entiers. Mais Pascal (1623–1662) a donné le moyen de mener ce calcul dans son Traité de la sommation des puissances numériques.

Il procède ainsi : par le triangle arithmétique, on a : \((n+1)^3=n^3+3n^2+3n+1\).

Donc successivement : \[\begin{aligned} 2^3&=(1+1)^3=1^3+3\times 1^2+3\times 1+1\\ 3^3&=(2+1)^3=2^3+3\times 2^2+3\times 2+1\\ &\vdots\\ n^3&=(n-1+1)^3=(n-1)^3+3(n-1)^2+3(n-1)+1\\ (n+1)^3&=\hphantom{(n+1)^3}=n^3+3n^2+3n+1\end{aligned}\]

En sommant membre à membre et en simplifiant, il vient alors :

\[(n+1)^3=1^3+3\sum_{i=1}^ni^2+3\sum_{i=1}^n i +n\quad\text{ou}\quad 3 \sum_{i=1}^ni^2=(n+1)^3-1-3\dfrac{n(n+1)}{2}-n\]

d’où \(\displaystyle\sum_{i=1}^n i^2=\dfrac{1}{6}n(n+1)(2n+1)\) et \(T_n=\dfrac{1}{6}n(n+1)(n+2)\cdotp\)²

Empilement en cube ?

On peut théoriquement entasser des boulets en cube mais, la stabilité n’étant pas garantie, les artilleurs préféraient la pyramide à base carrée : chaque étape étant un carré de \(n^2\) boulets, si le tas est d’arête \(n\), on aura : \(C_n=1+4+9+\cdots+n^2\), donc \(C_n=\dfrac{1}{6}n(n+1)(2n+1)\cdotp\)

D’autres tas stables sont possibles. En particulier ceux en forme de toits. Par exemple, au sommet une ligne de \(2\) boulets repose sur des intervalles d’un « rectangle » de \(2\) lignes de \(3\) boulets. Cet étage repose lui-même sur \(3\) lignes de \(4\) boulets. On dénombrera :

\(L_n^2=1\times2+2\times3+3\times4+\cdots+n(n+1)=\displaystyle\sum_{i=1}^n (i^2+i)=\dfrac{n(n+1)(n+2)}{3}\cdotp\)

Si la ligne de faîte est de 3 boulets :

\(L_n^3=1\times 3+2\times4+3\times5+\cdots+n(n+2)=\displaystyle\sum_{i=1}^n (i^2+2i)=\dfrac{n(n+1)(2n+7)}{6}\cdotp\)

Si la ligne de faîte est de \(q\) boulets :

\(L_n^q=1\times q+2\times (q+1)+3\times (q+2)+\cdots+n(n+q-1)=\displaystyle\sum_{i=1}^n (i^2+(q-1)i)=\dfrac{n(n+1)(2n+3q-2)}{6}\cdotp\)

Il suffit de dénombrer la ligne de faîte si les tas sont uniformes.³

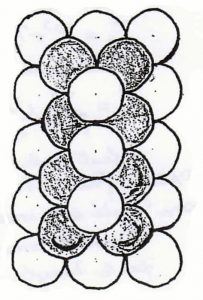
Cessons le tir ! Mais ne rendons pas les armes car, à la fin du  siècle fleurirent d’autres problèmes qui attendaient une réponse avec les nombres figurés et les nombres solides. Ce sont, par exemple, les questions d’emballage d’objets sphériques, de tubes d’acier, de bouteilles. Comment standardiser les contenants ? Comment perdre le moins de place dans la cale d’un navire et optimaliser la cargaison ? Et encore les molécules ne sont-elles pas un peu comme des sphères à entasser dans des schémas de composés chimiques ?

Franchement ces nombres ne sont pas encore bons à mettre au cabinet⁴.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Henry Plane, professeur de mathématiques retraité, est un membre actif de l’APMEP. Il appartient au groupe M:ATH (Mathématiques : Approche par des Textes Historiques) de l’IREM de Paris VII.