Les équerres d’Arenas
L’ingéniosité de la « géométrie pratique » des artisans au cours des siècles n’est plus à prouver. Mais qui connaît les équerres d’Arenas ? Bernard Parzysz les présente ici et fournit du même coup un terreau d’activités pour faire travailler la distinction entre géométrie instrumentée et géométrie démontrée au collège.
Bernard Parzysz
© APMEP Mars 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
L’art mudéjar s’est développé du XIIe à la fin du XVIe siècle dans les régions de la péninsule ibérique conquises par les royaumes chrétiens, en prolongeant les motifs et les techniques de l’art mozarabe qui l’avait précédé. En architecture, on y retrouve en particulier les plafonds à caissons en bois marquetés1 (fig. 1).
 (a) San Juan de los Reyes (Tolède) (© Jozef Sedmak, Dreamstime.com). |

(b) Casa de Pilatos (Séville) (© karoliinakazi.com). |
Ces plafonds, à l’instar des zelliges2 mauresques, comportent des motifs géométriques composés de rosaces à \(6\), \(8\), \(9\), \(10\), \(12\), \(16\) pétales qui se raccordent entre elles en formant des entrelacs. Pour réaliser le décor, les charpentiers ne faisaient pas de dessin d’ensemble et se contentaient de déterminer les types de rosaces qu’ils allaient utiliser, puis ils les mettaient en place à l’aide d’équerres de bois correspondant à ces rosaces.
Ces équerres triangulaires comportaient un angle droit et un angle aigu de \(\dfrac{\pi}{n\mathstrut}\), l’entier \(n\) correspondant à une rosace donnée.
Ils disposaient de tout un jeu d’équerres, pour diverses valeurs de \(n\), appelées « équerre de \(n\) » (fig.2).
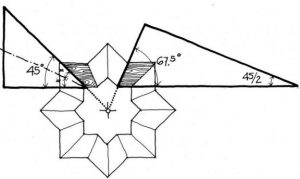
Figure 2 : Exemple d’utilisation des équerres de 4 et de 8 ↩ (© Enrique Nuere).
En 1619, au moment même où s’éteint l’art mudéjar, un architecte sévillan, Diego López de Arenas (1579— ?) commence à rédiger un « abrégé de charpenterie » [1] dans lequel il traite, entre autres, de la fabrication des plafonds (fig.3).
 |
 |
Il y indique, en introduction, mais sans donner d’explications, la façon de construire les équerres de \(n\) pour \(n=4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\), \(12\), \(14\), \(16\) et \(20\), comme triangles inscrits dans un demi-cercle (fig. 4a). La figure relative à l’équerre de \(5\) (fig. 4b) témoigne de la difficulté à interpréter certaines des illustrations.
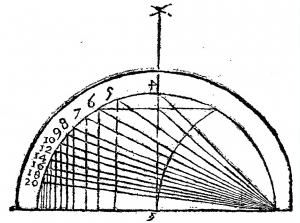
(a) Ensemble des équerres. ↩ |
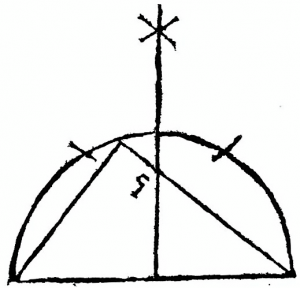
(b) Équerre de 5. ↩ |
Certaines de ces équerres sont obtenues par des constructions exactes « classiques » :
-
l’équerre de \(4\) n’est autre que le triangle rectangle isocèle (fig. 5a) ;
-
l’équerre de \(8\) se construit par bissection de celle de \(4\) (fig. 5b), et de même l’équerre de \(16\) par bissection de la précédente (fig. 5c) ;
-
l’équerre de \(6\) est un triangle rectangle \(30\)–\(60\) (fig. 5d) ;
-
l’équerre de \(12\) s’obtient par bissection de l’équerre de \(6\) (fig. 5e).
|
(a) Équerre de 4. ↩ |
(b) Équerre de 8. ↩ |
|
(c) Équerre de16. ↩ |
|
|
(d) Équerre de 6. ↩ |
(e) Équerre de 12. ↩ |
Il y a quelques années, Enrique Nuere Matauco s’est attaché à décrypter l’ouvrage d’Arenas [2] ; voici la construction qui ressort de son étude pour l’équerre de \(5\) (fig. 6) :
-
Partant du diamètre [AB], de milieu O, placer le sommet C d’un triangle équilatéral ABC.
-
Tracer la droite (OC).
-
Tracer le cercle de centre C et de rayon OA, qui coupe le segment [OC] au point D.
-
Tracer la droite (BD), qui recoupe le demi-cercle en E.
Le triangle ABE est une équerre de \(5\), c’est-à-dire que \(\widehat{\mathrm{ABE}}=\dfrac{\pi}{5}\cdotp\)
|
|
|
|
|
|
Qu’en est-il en réalité ? Prenant comme unité le rayon du demi-cercle, on a \(\mathrm{OC}=\sqrt{3}\) et \(\mathrm{CD}=1\), d’où \(\mathrm{OD}=\sqrt{3}-1\) et \(\widehat{\mathrm{ABE}}=\arctan(\sqrt{3}-1)\), soit \(\widehat{\mathrm{ABE}}\approx36,2\)° (au lieu de \(36\)°). Cet écart d’un cinquième de degré conduit à un écart systématique de \(2\) degrés en plus lorsqu’on reporte dix fois l’équerre autour d’un point pour réaliser une rosace, écart de l’ordre de celui qu’on commet en juxtaposant les équerres.
Remarque : la construction qui précède peut être utilisée pour obtenir un pentagone « presque régulier » inscrit dans un cercle ; en effet, [AE] sous-tend un arc de \(72,4\)° environ (au lieu de \(72\)°). On peut même en imaginer des variantes, comme par exemple celle-ci (fig. 7), qui n’utilise qu’une seule ouverture de compas :
-
Partant du diamètre [AB], de milieu O, tracer les cercles de centres A et B passant par O, qui coupent le demi-cercle respectivement en M et N.
-
Tracer les cercles de centres M et N passant par O, qui se recoupent en C.
-
Tracer le segment [OC].
-
Tracer le cercle de centre C passant par M, qui coupe [OC] en D.
-
Tracer la droite (BD), qui recoupe le demi-cercle en E.
|
|
|
|
|
|
|
|
|
|
|
|
Arenas obtient l’équerre de \(7\) par bissection du grand angle aigu de l’équerre de \(5\) (fig. 8). L’angle obtenu est donc d’environ \(26,9\)° (au lieu de \(25,7\)°), soit un écart de \(1,2\)° qui, reporté \(14\) fois pour la rosace, donnera une différence de plus de \(16\)°, ce qui n’est pas négligeable.
Figure 8 : Construction de l’équerre de 7. ↩
Antonia Redondo explique que « la clé est le rabotage, essentiel, des pièces de bois, permettant au charpentier de les ajuster à la forme requise, produisant finalement une rosace pratiquement régulière. »3 ([3], p. 75).
Pour l’équerre de \(9\), elle indique que « les explications d’Arenas sont incomplètes et inintelligibles »3 (ibid.). Elle conclut cependant, de l’analyse de l’une de ses illustrations, que la construction utilise le milieu du côté du demi-hexagone inscrit. On peut alors proposer la procédure suivante (fig. 9), qui commence comme la procédure alternative de la figure 6 :
-
Partant du diamètre [AB], de milieu O, tracer les cercles de centre A et B passant par O, qui coupent le demi-cercle respectivement en M et N.
-
Tracer les cercles de centres M et N passant par O, qui se recoupent en C.
-
Tracer les segments [MN] et [OC], qui se coupent en I.
-
Prolonger le segment [BI] jusqu’à son intersection, P, avec le demi-cercle.
-
Construire la bissectrice de l’angle \(\widehat{\text{ABP}}\), qui coupe le demi-cercle en Q.
Le triangle ABQ est une équerre de \(9\).
|
|
|
|
|
|
|
|
|
|
|
|
On a \(\widehat{\mathrm{ABQ}}=\dfrac{1}{2}\arctan\left(\dfrac{\sqrt{3}}{2}\right)\), soit \(\widehat{\mathrm{ABQ}}\approx20,45\)° (au lieu de \(20\)°). Le report de \(18\) équerres pour réaliser une rosace conduit alors à un écart de \(8\)° qui, ici aussi, peut être annulé grâce au rabotage de l’équerre.
Bien évidemment, les équerres de \(10\), de \(20\) et de \(14\) sont obtenues par bissection.
Le traité d’Arenas permet donc un accès direct aux pratiques des artisans et maîtres d’œuvre du XVII siècle et des siècles antérieurs. Leur géométrie « pratique » s’appuie certes sur la géométrie « savante », comme le montrent les constructions exactes mises en œuvre (équerres de \(4\), de \(6\), de \(8\), de \(12\), de \(16\)).
Mais la nécessité d’obtenir des solutions pour les cas qu’elle ne peut ou ne sait pas traiter conduit à inventer des solutions originales plus ou moins approchées. La problématique n’est pas ici celle de la conformité à une théorie (en l’occurrence la géométrie euclidienne) mais celle, pragmatique, de l’efficacité (« ça fonctionne »).
Les artisans étaient sans doute — au moins dans le cas des grands écarts — conscients du fait que leurs constructions n’étaient pas exactes, mais la construction géométrique leur permettait un dégrossissage de l’équerre de bois, celle-ci étant ensuite finalisée par des essais et un ponçage rectificatif.
Se pose également la question de l’invention de ces procédures approchées. Ce qui précède suggère qu’elles sont dérivées des procédures correspondant aux constructions exactes ; en particulier, l’illustration de la figure 4a permet d’imaginer un scénario. Partant de la configuration construite pour les équerres à construction exacte de \(4\) et de \(6\), c’est-à-dire le demi-carré et le demi-hexagone inscrits (fig. 10a), l’équerre de \(5\) correspondra à un point G du demi-cercle situé entre F et M. Une idée naturelle (fig. 10b) consiste à prolonger le segment [BI], où I est le milieu de [MN]. On obtient alors un point P, mais l’expérience montre que ce point est trop haut, et qu’il convient mieux — après bissection — pour l’équerre de \(9\) (voir figure 9). Il faut donc trouver un point G de l’axe (OC) situé plus bas que I, d’où l’idée de remplacer le segment [MN] par l’arc \(\overset{\displaystyle\frown}{\mathrm{MN}}\) du cercle centré en C (fig. 10c).
|
(a) |
|
|
(b) |
(c) |
Pour l’équerre de \(7\), l’idée d’une série de juxtapositions de l’autre angle aigu de l’équerre de \(5\) a pu amener à constater que \(7\) juxtapositions successives d’une équerre de \(5\) autour du sommet du grand angle aigu — symétrie par rapport à un côté — font un peu plus qu’un tour (fig. 11), et qu’en conséquence, en prenant la moitié de cet angle et en la rabotant un peu, on pourra obtenir une équerre de \(7\) acceptable.
Figure 11 : Vers l’équerre de 7. ↩
En conclusion, même s’ils sont souvent délicats à interpréter, les traités écrits par les artisans de jadis sont susceptibles de nous fournir des renseignements précieux sur leurs connaissances géométriques et sur les techniques mises en œuvre.
Ces techniques peuvent être réinvesties en classe, notamment au niveau du collège, d’une part pour travailler les procédures de construction à la règle et au compas sous forme d’algorithmes, et d’autre part pour mettre en évidence les limites des constructions approchées, à l’aide d’un logiciel de géométrie dont les constructions sont a priori extrêmement précises.
Dans l’exemple précédent, on peut constater que \(10\) juxtapositions d’une équerre de \(5\) autour du sommet de son angle « utile » font presque exactement un tour, mais qu’il y a malgré tout une petite différence (fig. 12a). Au contraire, le même traitement appliqué à une équerre de \(6\) ne fait apparaître aucun écart (fig.12b).
|
(a) |
|
(b) |
En allant plus loin on peut, en troisième, démontrer que l’équerre de \(5\) n’est pas exacte, en calculant la tangente de son angle « utile » : \(\sqrt{3}-1\), puis une valeur approchée de cet angle : \(36,206\)°.
La distinction entre géométrie instrumentée et géométrie démontrée est un enjeu important du programme de mathématiques du cycle 4, mais la mise en évidence de cette distinction n’est pas toujours facile, notamment en raison du fait que la résolution d’un problème de géométrie euclidienne utilise de fréquents allers et retours entre figure et raisonnement. On dispose, avec les équerres d’Arenas, d’un élément permettant d’opérer une différentiation nette entre les deux paradigmes, qui peut éventuellement servir de base à un travail interdisciplinaire autour d’un art original, relativement méconnu et cependant plus proche de nous qu’il n’y paraît : ainsi, le château de Villandry possède un plafond mudéjar du XV siècle, récupéré d’un palais de Tolède.
Bibliographie
-
Diego López de Arenas. Breve compendio de la carpinteria de lo blanco. http://www.sedhc.es/biblioteca/tratado.php?ID_pubD=26. Séville : L. Estupiñan, 1633. ↩
-
E. Nuere Matauco. La carpinteria de lo blanco. Lectura dibujada del primer manuscrito de López de Arenas. Madrid : Ministerio de Cultura, 1985. ↩
-
A. Redondo Buitrago. « On polygons, set squares and mudéjar carpentry ». In : Nexus 2018 : Architecture and Mathematics, Conference book (2018). Sous la dir. de K. Williams et M.G. Bevilacqua, p. 73-77. ↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Bernard Parzysz, professeur émérite de l’université d’Orléans, fait partie du Laboratoire de Didactique André Revuz de l’université Paris-Diderot. Il collabore depuis une dizaine d’années avec des archéologues pour retrouver les connaissances géométriques des artisans de l’Antiquité, notamment les mosaïstes.
![]()

-
L’idée initiale de cet article provient d’un exposé entendu lors d’un colloque sur l’architecture [3].↩
-
Les zelliges sont des mosaïques à motifs géométriques constituées de morceaux de faïence colorée. Les plus célèbres se trouvent à l’Alhambra de Grenade. Pour une utilisation des zelliges en classe, voir l’article « Zelliges à la grande mosquée de Strasbourg », de Julie Benoit, paru dans PLOT 58.↩
-
Traduction personnelle.↩

Une réflexion sur « Les équerres d’Arenas »
Les commentaires sont fermés.