Le musée de JSM
Le parcours proposé par notre illustrateur dans ce numéro tient à la fois du musée, du fil rouge et d’une démarche artistique qui lui est propre, et qu’il nous dévoile ici. Joli moment de rencontre entre mathématiques et arts.
Jean-Sébastien Masset
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Spirale
Je voulais faire une œuvre utilisant des principes ou objets mathématiques.
J’ai pensé au nombre d’or qui régit de nombreuses œuvres classiques et j’ai trouvé intéressant de l’utiliser dans une œuvre contemporaine.
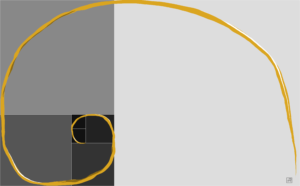
La suite de Fibonacci permet une approximation de ce nombre et la représentation en carrés successifs, comme sur cette image, est classique.
Cela permet de créer la spirale dite de Fibonacci représentée grossièrement ici en couleur « or ».
Les nuances de gris sont choisies en fonction de la valeur du carré dans la suite.
La valeur hexadécimale de la nuance est \(\mathsf{xxxxxx}\), où \(\mathsf{x}\) est la valeur du carré dans la suite. \(111111\) pour les deux plus petits, puis \(222222\), \(333333\), \(555555\), \(888888\) et enfin \(\mathsf{dddddd}\).
Jacques & frères
L’article illustré parle justement de la construction d’œuvres d’art. Ou plus précisément de principes utilisés dans leur construction, sans que cela ne soit évident dans l’œuvre elle-même.
Il y est entre autre question de musique, et de la façon dont un même thème musical est reproduit tout au long d’une œuvre de manières variées.
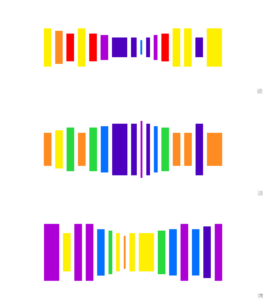
Chaque élément du triptyque représente graphiquement un même thème musical. Il s’agit de Frère Jacques, auquel j’ai retiré les répétitions.
Chaque note est représentée par une couleur, selon les couleurs de l’arc en ciel. Do en violet, ré en indigo, …, si en rouge. La hauteur de la bande de couleur est liée à la note également : plus la note est haute, plus la bande est petite, comme sur un xylophone. La différence de longueur de bande entre deux notes successives est deux fois plus longue si les notes sont séparées d’un ton que si elles sont séparées d’un demi-ton.
Les largeurs sont proportionnelles à la longueur de la note dans le morceau. Une blanche est deux fois plus large qu’une noire par exemple.
La première image représente donc Frère Jacques en commençant le morceau par un sol.
La deuxième image est le même morceau, en inverse. Lorsque le thème initial monte d’un ton, le thème inverse descend d’un ton. Pour que ça fonctionne, il commence par un la.
La troisième est le morceau repris à la quinte (donc commençant par do) et rétrograde.
Coalitions

Cela représente les coalitions possibles dans une assemblée à quatre groupes.
La couleur de fond est du noir appliqué avec 51 % d’opacité, symbole du poids nécessaire pour être gagnant dans un débat.
Dans le premier disque, chaque partie est remplie avec du noir avec un niveau d’opacité égal à son pourcentage d’occupation.
Dans les autres, j’ai mis des opacités égales aux poids des coalitions possibles. Une coalition est gagnante si son niveau de gris est plus foncé que le gris du fond de l’image.
Le dernier disque représente le cas où tous les groupes vont dans le même sens.
La poule ou le neuf ?

Je suis parti de la question de qui était là en premier, de la poule ou de l’œuf, en m’inspirant de la démarche de représenter une expression de la langue française.
Si l’on considère que l’image a un fond jaune sur lequel sont tracées les poules et les lignes noires (interprétation naturelle due à l’utilisation habituelle d’encre noire), les poules existent sur l’image mais les œufs ne sont pas réels car ils ne sont visibles que grâce aux lignes qui s’interrompent. D’une certaine façon, les poules valent \(1\) et les œufs \(0\). Soit \(1 001\) écrit dans l’image. Et \(1 001\), c’est neuf en binaire. Tout commence avec un neuf. Un neuf, un œuf…
D’ailleurs qui existe vraiment sur l’image ? Peut-être que le fond est noir et qu’on a tracé dessus des œufs et des lignes jaunes. Auquel cas ce sont les poules qui n’existent pas vraiment. Donc on ne sait pas qui est là en premier.
On peut tourner la question dans tous les sens, elle n’a pas de réponse.
Et si l’on retourne l’image à 180°, elle ne change pas d’un iota, la tourner n’apporte pas de réponse.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Jean-Sébastien Masset est l’un de nos trois illustrateurs, le seul qui ne soit pas aussi prof de math. Mais c’en est un véritable amateur! Magicien et mentaliste de son état, homme aux multiples talents, vous pouvez le contacter si vous avez des projets (illustrations, animations, …). Vous pouvez également retrouver certaines de ses créations sur Facebook (Jean-Sébastien Masset).
![]()

Une réflexion sur « Le musée de JSM »
Les commentaires sont fermés.