Atelier Math et anamorphoses
Avec des collègues de son lycée, Mireille Génin a animé un atelier scientifique pendant une quinzaine d’années, atelier au cours duquel elle a pu observer, découvrir… des mathématiques et des élèves pleins d’idées et de passion. Voici le récit d’une de leurs découvertes au cours de l’année 2001 : la recherche rendue accessible en somme !
Mireille Génin
© APMEP Mars 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
L’atelier s’intégrait dans le cadre administratif des Ateliers Scientifiques et Techniques ![]() . Nous l’avions intitulé : Atelier Mathématiques appliquées. Les animateurs étaient des professeurs de l’équipe de mathématiques du lycée ; les élèves, volontaires, pouvaient appartenir à n’importe quelle classe. Il nous est même arrivé parfois d’accueillir un ou deux élèves d’autres lycées au rythme d’une séance hebdomadaire d’une heure et demie. À cela s’ajoutait la participation au cours de l’année à la Fête de La Science, au Village des Sciences, à Exposcience et au Salon Culture et Jeux Mathématiques
. Nous l’avions intitulé : Atelier Mathématiques appliquées. Les animateurs étaient des professeurs de l’équipe de mathématiques du lycée ; les élèves, volontaires, pouvaient appartenir à n’importe quelle classe. Il nous est même arrivé parfois d’accueillir un ou deux élèves d’autres lycées au rythme d’une séance hebdomadaire d’une heure et demie. À cela s’ajoutait la participation au cours de l’année à la Fête de La Science, au Village des Sciences, à Exposcience et au Salon Culture et Jeux Mathématiques ![]() .
.
Mathématiques expérimentales, expérimentées : les recherches avançaient au gré des questions, des rebondissements, des découvertes, des rencontres. Le plus souvent, les animateurs de l’atelier ne savaient pas où iraient les recherches engagées, les élèves en étaient conscients et cela les motivait encore davantage !
Miroirs cylindriques et anamorphoses
Le sujet qui nous intéresse ici débute lors de la visite d’un groupe d’élèves à l’un des premiers Salons Culture et Jeux Mathématiques où un stand présentait de nombreuses anamorphoses : images dans des miroirs sphériques, cylindriques ou coniques. Nous avons eu du mal à détacher Hervé, élève de Seconde, de ce stand durant nos trois jours sur le salon. L’animateur du stand, très patient, répondait à toutes ses questions et en récompense pour son intérêt lui offrit en fin de salon l’un de ses « miroirs » : un petit cylindre métallique d’une dizaine de centimètres de haut et \(2\) ou \(3\) cm de diamètre… C’est ce cylindre qui fut le point de départ de recherches très riches dans l’atelier, l’année scolaire suivante.
Pour commencer les recherches et expérimentations, le cylindre rapporté par Hervé étant un peu petit pour bien visualiser les expériences, nous trouvons des grandes boîtes cylindriques pouvant faire miroir, en fait des boîtes de rangements très bon marché, vendues à l’origine pour ranger les rouleaux de papier toilette ! On peut faire des maths avec tout !

Figure 1. Miroir de départ. |

Figure 2. Boîte miroir et le miroir d’Hervé. |
Les élèves intéressés par le sujet sont alors en début de 1ère S. Leurs premiers essais sont peu structurés. Ils commencent par des dessins dont ils observent l’image déformée dans le miroir.
Dans le livre Secrets des anamorphoses (éditions Gallimard jeunesse, 1996), ils trouvent des grilles permettant de fabriquer des anamorphoses cylindriques mais cela ne les satisfait pas.
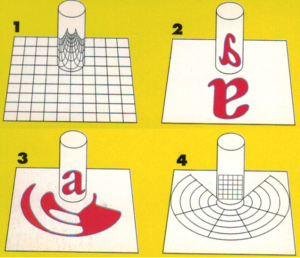
Figure 3. Secrets des anamorphoses.
Leur projet se précise assez vite : « Partir d’une figure géométrique dont les propriétés sont clairement identifiées (carrés, polygones réguliers, cercles…), transformer cette figure avec la transformation adéquate qu’ils vont créer avec le logiciel de géométrie dynamique1, puis présenter la feuille devant le miroir pour retrouver l’image de départ ».

Figure 4. Test pour un hexagone.
En Seconde, les élèves avaient étudié une transformation qui ne conserve pas l’alignement : une symétrie par rapport à un cercle2. Cette transformation, que les élèves nommaient \(\mathbf{z}\) est définie par :
Soit \((C)\) un cercle donné de centre \(\mathrm{O}\). Pour tout point \(\mathrm{M}\) (distinct de \(\mathrm{O}\)), on construit la demi-droite \([\mathrm{OM})\). On marque le point d’intersection de \([\mathrm{OM})\) avec le cercle \((C)\) ; l’image \(\mathrm{M}’ ;\) du point \(\mathrm{M}\) par \(\mathbf{z}\) est alors le symétrique de \(\mathrm{M}\) par rapport à ce point d’intersection.
Figure 5. Première transformation : symétrie par rapport à un cercle.
À cette étape, nos apprentis chercheurs pensent que cette transformation va résoudre leur problème d’image. À l’aide du logiciel , ils transforment un point et créent pour cela une macro-construction3. Lorsque le point parcourt l’un des objets dont ils veulent étudier l’image, l’outil Lieu leur permet de tracer cette image. Il reste à poser la feuille de la figure devant le miroir pour retrouver, si tout va bien, l’objet de départ. Mais visiblement, la transformation ne répond pas à leurs attentes…

Figure 7. Image réfléchie par le miroir. |
Peu convaincus par les résultats observés (dans le miroir la tête devrait être ronde !), les lois de la réflexion de Descartes, vues en sciences physiques, sont appelées à la rescousse :
Figure 8. Réflexion miroir plan.
Comment les adapter au miroir cylindrique ?
L’idée vient de s’intéresser au cercle que le miroir dessine sur la table et d’utiliser une tangente au cercle ; mais laquelle ? L’œil leur pose problème. Une nouvelle transformation est alors testée par Hervé qui dit que la position de l’œil aura peu d’importance : ce sera à l’observateur de le positionner correctement en se déplaçant ! D’où la transformation proposée.
Figure 9. Une nouvelle transformation.
Une nouvelle macro-construction est ainsi créée :
|
Objets initiaux : |
Cette macro-construction et l’outil Lieu permettent d’obtenir les tracés qui sont ensuite testés avec les miroirs. Les figures créées par les élèves sont constituées de segments, arcs de cercles ou polygones réguliers mais leur imagination foisonne :
|
Figure 10. Transformation d’une grille. |

Figure 11. Image reformée dans le miroir. |
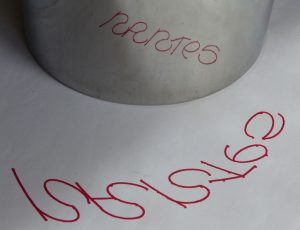
Figure 12. Essai élève, des lettres géométriques. |

Figure 13. Mary Poppins ! |
Poursuite de l’aventure sur des chemins différents
Les anamorphoses dans notre quotidien
Ce chemin nous mène à la visite de l’entreprise Pack-system, installée près de Nantes. C’est une entreprise de fabrication d’emballages qui utilise des anamorphoses pour les emballages emboutis : à partir d’un dessin « rectangulaire » (texte, illustration, code-barre…) représenté sur un emballage « plat », il s’agit d’appliquer une déformation sur la pièce pour retrouver le rendu escompté sur le cylindre final (la boîte de conserve). C’est donc un dessin anamorphosé qui doit y être imprimé. Le dessin apparaissant déformé sera « remis en forme » après l’emboutissage ![]() . Les entreprises utilisant ce procédé de fabrication parlent d’impression prédéformée. Pour elles, pas de logiciel de géométrie dynamique mais des calculs de grilles pour passer d’une image « déformée » à une image « reformée ». Les difficultés se posent particulièrement pour les informations écrites sur les côtés de la boîte qui doivent être lisibles après l’emboutissage.
. Les entreprises utilisant ce procédé de fabrication parlent d’impression prédéformée. Pour elles, pas de logiciel de géométrie dynamique mais des calculs de grilles pour passer d’une image « déformée » à une image « reformée ». Les difficultés se posent particulièrement pour les informations écrites sur les côtés de la boîte qui doivent être lisibles après l’emboutissage.

Figure 14. L’image sur la plaque déformée AVANT l’emboutissage. |

Figure 15. L’image reformée APRÈS l’emboutissage. |
Les anamorphoses coniques, pour aller encore plus loin
Cette fois-ci les miroirs sont réalisés avec du papier miroir, ils sont beaucoup plus petits. L’observateur se positionne au-dessus du miroir (œil sur l’axe vertical).

Figure 16. Miroirs coniques.
Les élèves dessinent d’abord une coupe verticale du miroir cône (le triangle \(\mathsf{OSA}\) sur la coupe suivante) et reconstituent le schéma optique de la réflexion.
Dans ce cas de figure, ils peinent à trouver la transformation qui permettrait de faire avancer le problème. Certains d’entre eux se souviennent que sur le stand du Salon, l’animateur présentait une « machine à transformer les figures » basée sur une homothétie. Mais quelle homothétie ? De quel centre et de quel rapport ?
Pour « voir » une homothétie qui transformerait \(\mathsf{M}\) en \(\mathsf{M}’ \), il faudrait avoir des parallèles ou une configuration de Thalès. La figure résiste et on aimerait bien que la droite \((\mathsf{ME})\) et l’axe \((\mathsf{OS})\) du cône soient parallèles ! Qu’à cela ne tienne, on décide qu’elles le sont : pour les physiciens, cela ne pose aucune difficulté, l’œil \(\mathsf{E}\) est assez « haut » par rapport à la hauteur du cône, pour pouvoir écrire : \((\mathsf{OS})//(\mathsf{ME})\). Pour le professeur de mathématiques, il y a beaucoup d’hésitations… On essaie quand même avec cette « simplification ».
La figure est alors plus intéressante pour faire avancer les recherches :
L’homothétie recherchée pour transformer \(\mathsf{M}\) en \(\mathsf{M}’ \) pourrait être de centre \(\mathsf{A}\), son rapport serait négatif et il faudrait montrer que le rapport ne dépend pas de la position de \(\mathsf{M}\) sur le segment \([\mathsf{OA}]\). Les élèves utilisent les outils de calcul du logiciel pour conjecturer des égalités. Au cours de leurs essais, ils s’aperçoivent qu’il y a des rapports de distances qui restent constants et que le rapport de l’homothétie cherchée ne dépend que des deux paramètres : \(h\) hauteur du cône et \(r\) rayon de la base, c’est-à-dire \(\mathsf{OS}\) et \(\mathsf{OA}\).
Ils établissent que \(\dfrac{\mathsf{IM}}{\mathsf{IM}’ }=\dfrac{\mathsf{AM}}{\mathsf{AM}’ }\cdotp\)
Un peu de trigonométrie dans les triangles \(\mathsf{SOA}\) et \(\mathsf{IMM}’ \) est alors utile. On note \(\alpha\) l’angle \(\widehat{\mathsf{OSA}}\), l’angle \(\widehat{\mathsf{MIM}’ }\) est alors \(2\alpha\) et \(\dfrac{\mathsf{IM}}{\mathsf{IM}’ }=\cos(2\alpha)\). Or le chapitre concernant le cosinus de l’angle double vient d’être étudié par les élèves de 1ère S. Ils trouvent alors : \(\dfrac{\mathsf{AM}}{\mathsf{AM}’ }=\cos^2(\alpha)-\sin^2(\alpha)\) et en observant l’angle \(\alpha\) du triangle \(\mathsf{SOA}\) : \[\dfrac{\mathsf{AM}}{\mathsf{AM}’ }=
\dfrac{h^2}{h^2+r^2}-\dfrac{r^2}{h^2+r^2}\cdotp\] D’où \(\dfrac{\mathsf{AM}’ }{\mathsf{AM}}=\dfrac{h^2+r^2}{h^2-r^2}\) et donc un rapport d’homothétie négatif : \(k=-\dfrac{h^2+r^2}{h^2-r^2}\cdotp\)
\(\mathsf{M}’\) est l’image de \(\mathsf{M}\) par l’homothétie de centre \(\mathsf{A}\) et de rapport \(k\). Cette propriété étant vraie pour tous les points \(\mathsf{M}\) à l’intérieur du cercle de base du cône, une nouvelle macro-construction est créée et enregistrée, les élèves la nomment Anacône :
Macro-construction Anacône |
| Objets initiaux : Le cercle de centre \(\mathsf{O}\) de rayon \(r\), un nombre pour la hauteur \(h\) du cône, le point à transformer \(\mathsf{M}\) Objets finaux : le point image \(\mathsf{M}’ \) Construction et calcul : la demi-droite \([\mathsf{OM})\), son point d’intersection \(\mathsf{A}\) avec le cercle, le calcul du rapport de l’homothétie, l’image \(\mathsf{M}’ \) de \(\mathsf{M}\) par l’homothétie de centre \(\mathsf{A}\) et de rapport le rapport calculé. |
On peut reprendre alors les tests avec cette macro et l’outil Lieu, et ça fonctionne !
|
Figure 19. Transformation d’une grille pour un miroir conique. |
Figure 20. Transformation d’un cœur pour un miroir conique. |
En conclusion
Toutes ces recherches prennent du temps, mais cette contrainte n’est pas un souci dans un atelier. La plus grande difficulté est que les élèves ne se découragent pas et qu’ils puissent se remotiver après un échec pour explorer de nouvelles pistes. Peu d’élèves sont allés jusqu’à une synthèse écrite de leurs travaux de recherche mais tous se sont impliqués dans les présentations orales de leur cheminement et découvertes lors de villages des sciences, portes ouvertes et salons scientifiques.
Quelques années après, Hervé raconte :
« Je me souviens bien de ce miroir cylindrique, je l’ai toujours sur mon bureau (d’ailleurs, en le mesurant, c’est \(10\,\text{cm}\) de hauteur et \(31\) ou \(32\,\text{mm}\) de diamètre). J’avais passé de très belles années à l’atelier, je me souviens de l’ambiance détendue et relâchée qui y régnait, et des quelques visites que nous avons faites à Paris pour le salon de la FFJM, de l’équipe qui concourait pour la coupe. Je me souviens que les élèves étaient assez moteurs de cet atelier, les sujets d’étude n’étaient pas imposés (même s’il y avait sans doute une petite orientation, j’imagine). Souvent, c’était des choses que nous avions vues sur un salon, comme ce qui est présenté dans cet article ou notre étude des tas de sable. Je me souviens avoir été fasciné par ces anamorphoses et d’avoir passé la journée à poser des questions à la personne qui animait le stand. »
Quelques pistes pour approfondir le sujet sur les anamorphoses cylindriques
-
une anamorphose cylindrique monumentale L’arroseur arrosé, œuvre de Claude Gazier, située à Lyon, à l’angle de la rue Cotte et la rue Narvick, 8 arrondissement
 .
.
Figure 21. L’arroseur arrosé, œuvre de Claude Gazier.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Mireille Génin, désormais retraitée, a été enseignante de mathématiques et formatrice pour les professeurs stagiaires. Elle reste active au sein de la régionale de Nantes de l’APMEP et fait partie de l’équipe d’Au fil des maths.

-
Les travaux des élèves ont été réalisés avec Cabri II, ils sont facilement adaptables pour être réalisés avec Geogebra.↩
-
Transformation présentée dans un article très intéressant de collègues de l’IREM de Rouen, publié en 1993 dans MATHS EN SECONDE : Énoncés et Scénarios, Bulletin Inter-IREM-SECOND CYCLE
 .↩
.↩ -
Créer une macro-construction dans permet d’enregistrer une construction qui pourra devenir un nouvel outil (comme une transformation). L’équivalent dans est
Créer un nouvel outil.↩
