Les représentations en barres :
« ni cet excès d’honneur, ni cette indignité »¹

Richard Cabassut propose un point de vue sur les avantages et les inconvénients des représentations en barre dans la résolution de problèmes, au moment où cette approche se développe dans les formations continues et les ressources proposées aux enseignants de l’école primaire.

Richard Cabassut

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Avertissement
Comme indiqué dans le revue papier, la bibliographie complète est accessible à la fin de cet article. Les renvois bibliographiques du texte qui suit ne citent que les auteurs (et, éventuellement, l’année).

Nous étudions ici les représentations en barres utilisées pour la résolution de problèmes arithmétiques élémentaires dès l’école primaire. Nous rappellerons d’abord une définition possible des représentations en barres et le contexte dans lequel ces représentations se développent actuellement. Ensuite nous discuterons de quelques avantages et inconvénients attribués à ces représentations.

Une première définition des représentations en barres

Commençons par une définition sommaire des représentations en barres sachant qu’il existe des points de vue différents comme ce sera évoqué plus loin.

Pour cela nous allons partir de l’exemple suivant d’énoncé de problème arithmétique inspiré de [21] pour lequel il n’est pas question ici de discuter de la pertinence de l’énoncé ou de la recevabilité de la rédaction de la solution.

Enoncé 1
Une vache pèse 150 kg de plus qu’un chien. Une chèvre pèse 130 kg de moins qu’une vache. Ensemble les animaux pèsent 410 kg. Combien pèse le chien ?

Voici un premier exemple de représentations en barres qu’on peut associer à ce problème :

Puis à partir de cette représentation, une rédaction possible d’une solution pourrait être la suivante. \begin{align*}
\text{poids du chien}+\text{poids de la vache}+\text{poids de la chèvre} &=410\\
\text{poids du chien}+150 &=\text{poids de la vache}\\
&=\text{poids de la chèvre}+130\\
3\text{ poids de la vache} &=410+150+130\\
&=690\\
\text{poids de la vache} &=690\div3\\
&=230\\
\text{poids du chien} &=\text{poids de la vache}-150\\
&=230-150\\
&=80
\end{align*}
Le poids du chien est \( {80}\) kg.

Voici un autre exemple de représentation en barres qu’on peut associer à ce problème, ce qui illustre qu’il peut y avoir diverses représentations en barres d’un même problème.

Puis à partir de cette représentation, une rédaction possible d’une solution pourrait être la suivante : \[\begin{aligned}
3\text{ poids du chien}+150+20 & =410\\
3\text{ poids du chien} & =410-170\\
& =240\\
\text{poids du chien}& =240\div3\\
& =80\end{aligned}\] Le poids du chien est \( {80}\) kg.

Étudions les caractéristiques de ces représentations.

Une barre ou rectangle représente une grandeur (ici le poids) attachée à un objet (ici un animal). À l’intérieur de la barre, on indique une mesure de la grandeur qu’elle représente (si elle est connue), ou un point d’interrogation si elle est inconnue.

Les rectangles ont une « largeur » fixe et une « longueur » variable. Cette longueur variable n’a pas à être proportionnelle à la grandeur ; ce point de vue n’est pas partagé par tous les auteurs [15], sauf dans les problèmes de partage en parts égales. L’usage veut qu’on respecte l’ordre des grandeurs : un poids de \( {150}\) kg sera représenté par une barre plus longue qu’un poids de \( {130}\) kg. On voit la difficulté lorsque les barres représentent des grandeurs inconnues. C’est pourquoi les usages sur l’ordre (et à plus forte raison sur la proportionnalité) peuvent ne pas être respectés.

En général, les rectangles sont représentés horizontalement pour la «longueur» variable et les «largeurs» fixes sont alignées verticalement ou juxtaposées. Cependant, on peut permuter vertical et horizontal pour certaines représentations.

Des représentations additionnelles (sur notre exemple les flèches à deux sens) peuvent indiquer les écarts entre deux barres et représentent donc une augmentation ou une diminution d’une barre par rapport à une autre. Elles peuvent également indiquer une mesure de la grandeur représentée par la réunion de barres : accolade verticale (dans notre exemple, \(410\) pour la réunion des trois poids d’animaux) ou horizontale (au-dessus de barres juxtaposées). Il est d’usage d’indiquer la mesure au regard de la flèche à deux sens qui la représente (et éventuellement un point d’interrogation si cette mesure est inconnue). Dans d’autres représentations, ces accolades peuvent être remplacées par des flèches à deux sens.

Des légendes donnent des informations sur ce que représente un rectangle (dans notre exemple, l’animal considéré : chien, vache ou chèvre) ou sur l’étape de représentation (souvent avant et après un événement, ou dans notre exemple représentation initiale et représentation intermédiaire).

Quelques types basiques des représentations en barres

Seront d’un même type des problèmes qui seront semblables du point de vue d’un critère : le critère peut être lié à la forme de l’énoncé, aux solutions possibles, aux difficultés attendues… Il y a de multiples catégorisations possibles [3]. Avec la terminologie de Houdement de la catégorisation en problèmes basiques, complexes et atypiques², considérons les trois catégories de problèmes arithmétiques basiques suivant leurs représentations en barres d’après [21] :

les problèmes parties-tout :

Ce schéma représente la relation mathématique suivante :

\(\text{mesure de la partie 1}\)
\(+\text{mesure de la partie 2}\)
\(=\text{mesure du tout}\).
les problèmes de comparaison :

Ce schéma représente la relation mathématique suivante :

\(\text{petite mesure}+\text{différence}=\text{grande mesure}\).
les problèmes de partage en parts égales (appelés par Ng et Lee «problèmes de multiplication et de division»).

Ce schéma représente la relation mathématique suivante :

\(n \times\text{mesure d’une part}=\text{mesure du tout}\).

Les problèmes complexes se décomposent en ces problèmes basiques. Dans notre exemple complexe introductif, dans la seconde solution on voit qu’apparaissent deux problèmes de comparaison (entre la vache et le chien, entre la vache et la chèvre), un problème de parts égales (en reconnaissant \(3\) parts égales de poids chien), puis un problème parties-tout en décomposant le tout (\(410\)) en parties.

Mais la catégorisation des problèmes basiques dans les représentations en barres ne fait pas l’unanimité, même à Singapour. Kaur considère la catégorie parties-tout en y incluant la catégorie précédente de partage en parts égales [16].

En effet on peut considérer que ce dernier cas modélise ce qu’on appelle l’addition itérée, c’est-à-dire que le tout est la réunion de parties représentées par des parts égales. La seconde catégorie est celle des comparaisons absolues entre objets (différents ou ayant subi une variation), comme pour Ng et Lee. La différence apparaît avec la troisième catégorie, les problèmes de variation (change model) : Kaur compare des variations du même objet, variations additives (ajout ou retrait) ou multiplicatives (coefficient multiplicatif supérieur à \(1\) pour une augmentation ou inférieur à \(1\) pour une diminution). Dans cette catégorie, on retrouve les catégories de Vergnaud correspondant aux transformations d’état [29] pour les variations absolues et au coefficient multiplicatif dans un seul espace de mesures [28] pour les variations relatives. Pour Kaur, la diminution ou l’augmentation sont représentées par une valeur absolue dans le cas d’une variation absolue ou une fraction ou un pourcentage de la mesure initiale dans le cas d’une variation relative. Illustrons cette catégorie sur des exemples inspirés de Kaur.

L’augmentation est de \(12\).

L’augmentation est de \(\dfrac{2}{3}\) de la valeur initiale.

La diminution est de \(30\) % de la valeur initiale.

Après avoir détaillé ces deux catégorisations différentes émanant de Singapouriens, on ne s’étonnera pas que les catégorisations proposées par les différents éditeurs français soient également variées. Chaque catégorisation de problèmes propose ses types de modèles à reconnaître pour résoudre un problème donné, ce qui nous amène maintenant à rappeler la distinction entre représentation et modélisation.

Distinction entre représentation et modélisation

Il n’aura pas échappé au lecteur avisé que nous avons évoqué jusqu’à présent la représentation en barres et non pas la modélisation en barres. Pourtant à Singapour [21], cette représentation en barres est appelée «la méthode de modélisation» (the model method). Notre intention est bien de distinguer représentation et modélisation, qui sont d’ailleurs distinguées par deux compétences différentes dans les programmes officiels de la scolarité obligatoire française. Parzysz [23] distingue dessin et figure. Le dessin est une représentation perceptive (la perception pouvant être altérée par l’affectif) alors que la figure est un dessin dans lequel on intègre des connaissances : on regarde le dessin du terrain de football avec ses connaissances et on « voit » que les côtés opposés sont de longueurs égales, les quatre angles des corners sont droits et on voit donc que les diagonales vont se couper en leur milieu ou qu’elles sont de longueurs égales. On pourrait dire en généralisant que la modélisation est à la représentation ce que la figure est au dessin.

En d’autres termes quand on regarde une représentation en y mettant des relations mathématiques entre éléments représentés, on modélise mathématiquement. Un modèle mathématique d’un système d’éléments représentés est un système de relations mathématiques entre éléments du système. Pour les problèmes arithmétiques élémentaires considérés dans cet article, on se limite aux relations mathématiques issues des quatre opérations élémentaires entre mesures de grandeurs représentées.

La modélisation mathématique ou mathématisation est une représentation dans laquelle les relations mathématiques entre différents éléments représentés sont reconnues et mises en évidence, à raison si le modèle est correct, à tort s’il est incorrect (voir plus loin un exemple de modélisation incorrecte).

La reconnaissance des relations mathématiques entre des éléments fait passer d’une simple représentation à une modélisation. Dans l’exemple précédent :

\[\text{« poids du chien}+150 = \text{poids de la vache »}\]

est une relation mathématique additive entre les poids du chien et de la vache. On peut représenter cette relation par l’écriture algébrique précédente, ou par la représentation en barres suivante :

Avec les représentations de Vergnaud on aurait représenté comme suit :

C’est le même modèle mathématique \[\text{« poids du chien}+150=\text{poids de la vache »}\] qui est visé par les deux représentations, en barres et de Vergnaud.

Ce n’est pas le fait de dessiner des rectangles pour la représentation en barres, ou des carrés et cercles, pour la représentation de Vergnaud, qui garantit la reconnaissance du bon modèle, et nous n’avons pas trouvé de résultats de la recherche qui montraient qu’une représentation rendait la modélisation plus facile qu’avec une autre représentation. Duval [10] a montré que les représentations d’un même objet ne sont pas toujours congruentes entre elles, et il est possible que pour certains élèves et certains problèmes, on puisse montrer que la reconnaissance d’un modèle, dans ces cas précis, est plus facile avec une représentation plutôt qu’avec une autre.

Enfin le recours à une représentation ne garantit pas la bonne modélisation, comme l’illustre l’exemple suivant inspiré de Sander [26].

Enoncé 2
Tu as acheté \(4\) pommes et \(5\) oranges. Combien de fruits as-tu en tout ?

Une représentation en barres peut être :

Elle conduit au modèle additif : \( ?=4+5=9\). Il y a \(9\) fruits.

Considérons l’énoncé suivant.

Enoncé 3
Chaque fois que tu achètes \(4\) pommes, tu as en cadeau \(1\) orange. À la fin des achats tu as \(5\) oranges. Combien de fruits as-tu en tout ?

Il peut conduire à la même représentation en barres et modélisation que précédemment, mais cette fois-ci, la modélisation est incorrecte.

Ce qui est donc fondamental dans la modélisation, c’est la justification du choix des relations mathématiques entre les éléments du système représenté. Pour justifier ces choix, l’élève doit produire deux types de raisonnements. D’une part, les raisonnements heuristiques [11] [25] permettent d’avoir des idées (qu’on espère bonnes) et de reconnaître des modèles (qu’on souhaite corrects). C’est par exemple les raisonnements de plausibilité construits sur le modèle suivant : (si A alors B) est vrai et B est vrai, donc A est davantage plausible [4]. Ces raisonnements sont très importants pour formuler des conjectures. D’autre part, des raisonnements de preuve valident le choix des relations mathématiques entre les éléments du système représenté et la validation du traitement mathématique de ces relations (ici essentiellement la validation de calculs). C’est par exemple la cas des raisonnements de nécessité basés sur le modèle suivant : (si A alors B) est vrai et A est vrai, donc B est nécessairement vrai.

C’est pourquoi nous distinguons représentation et modélisation : la modélisation est un cas particulier de représentation où les raisonnements heuristiques et de validation justifient les relations mathématiques entre objets représentés. .

Examinons maintenant le contexte qui explique le développement actuel des représentations en barres.

Le contexte du développement des représentations en barres

Chambris [5] note que les représentations en barres sont présentes dans l’enseignement français dans les années 70 mais c’est certainement à Singapour, en 1983, que les représentations en barres ont connu un développement massif, puisqu’elles sont devenues les représentations à utiliser, dans le curriculum officiel de cet état, pour résoudre les problèmes arithmétiques élémentaires. [16]. La commission Torossian-Villani [27] met en valeur Singapour, qui d’ailleurs obtient de bons résultats à TIMSS et PISA, et considère que sa méthode est basée sur des pédagogies efficaces, parmi lesquelles l’utilisation des représentations en barres. Neagoy a participé à cette commission et, comme directrice de collection, à la conception de la collection « Maths méthode de Singapour » de la Librairie des Écoles. Elle est également formatrice sur ce thème. D’ailleurs, plusieurs éditeurs scolaires français proposent des ouvrages se réclamant de la méthode de Singapour (la Librairie des Écoles , Larousse , Hachette , Bordas ). Enfin un thème de formation des référents mathématiques de circonscription pour 2019-2020 concerne les représentations en barres dans la résolution de problèmes. Nous sommes donc dans un contexte de développement de la diffusion des représentations en barres à l’école primaire française.

Discussion sur les avantages et les inconvénients des représentations en barres.

La première critique concerne l’efficacité de l’utilisation des représentations en barres. On peut d’abord remarquer qu’associer les bons résultats d’un pays à PISA ou à TIMSS, comme c’est le cas pour Singapour, n’est pas une garantie de cette efficacité. On sait par exemple que l’académie de Rennes a des meilleurs résultats que l’académie de Créteil au baccalauréat alors que c’est la même organisation scolaire, les mêmes programmes, les mêmes manuels, et en théorie la même formation de professeurs. L’explication est essentiellement socio-culturelle et sociologique. Par exemple, l’académie de Créteil connaît des difficultés pour recruter des professeurs d’école. Plus généralement une mauvaise réforme de la formation des maîtres et de leur recrutement peut avoir un impact plus redoutable sur les résultats à PISA et TIMSS que l’introduction d’une représentation en barres. Enfin la ville-état de Singapour et la France ont sans doute des niveaux de codétermination didactique [2] extra-mathématiques liés à la civilisation, à la société, à l’école et à la pédagogie très différents.
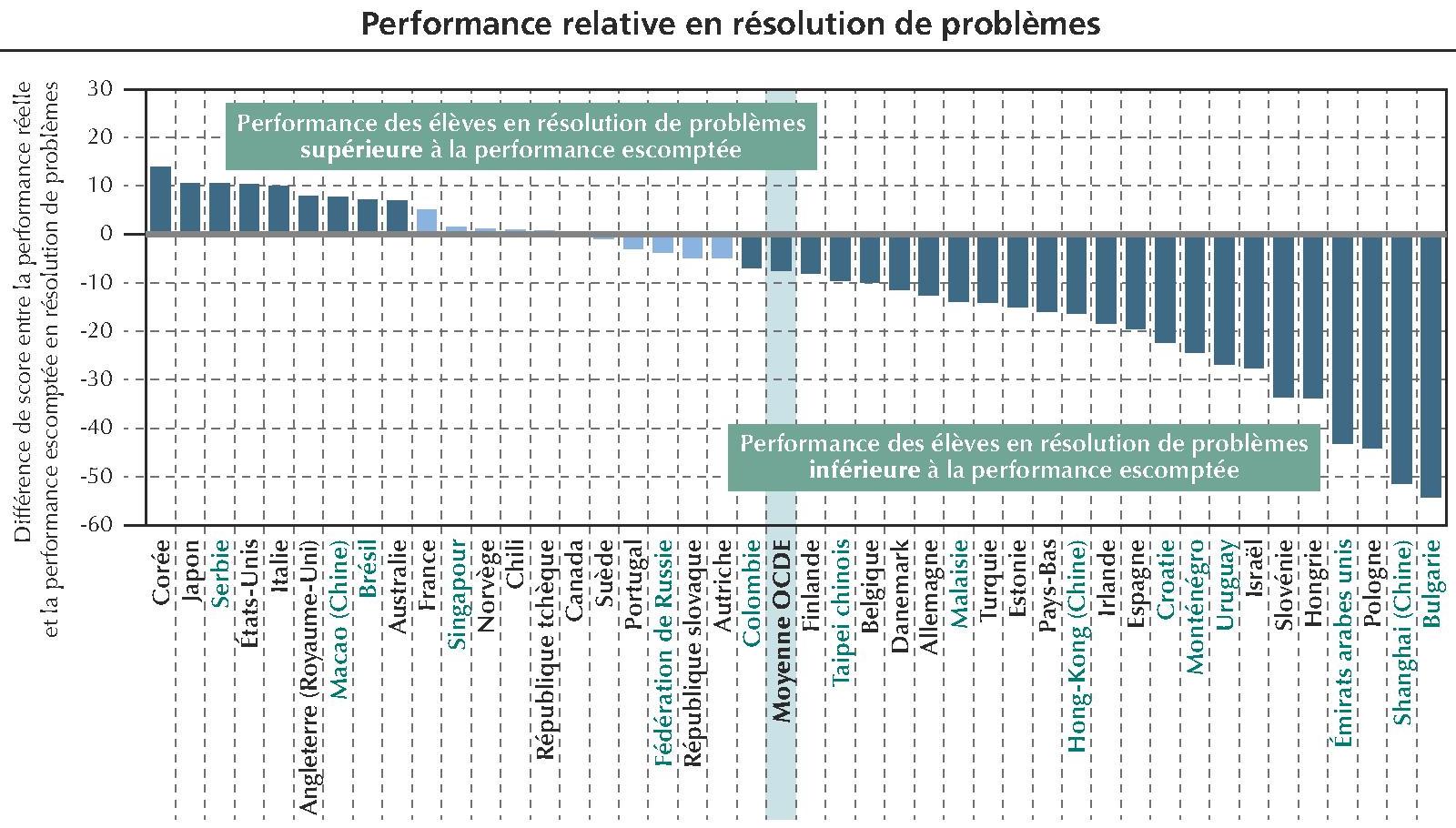
Chambris [6] note par exemple que les professeurs de Singapour ont \(100\) h de formation continue par an. Compte tenu de la variabilité liée au professeur, aux élèves, au contexte, « existe-t-il vraiment des pédagogies efficaces ? » [1]. En dehors des évaluations internationales et nationales qui peuvent être des indicateurs d’efficacité, nous n’avons pas trouvé de rapports de l’Inspection de l’Éducation nationale, ou des résultats de la recherche indiquant une meilleure efficacité des représentations en barres par rapport à d’autres représentations pour la résolution de problèmes arithmétiques. Je voudrais enfin terminer par une anecdote provocatrice, illustrant qu’on peut faire dire aux statistiques ce que l’on veut. Dans l’enquête PISA de 2012 [22] sur la résolution de problèmes, la France était classée avant Singapour. On aurait pu alors, à l’époque, conseiller à Singapour d’abandonner les représentations en barres au profit des représentations utilisées en France pour la résolution de problèmes.

Source : base de données PISA 2012, tableau V.2.6. [22].

Une autre critique concerne le caractère dominant que pourraient avoir les représentations en barres au détriment d’autres représentations. Même Neagoy, promotrice de l’utilisation des représentations en barres, insiste sur l’importance des représentations multiples :« L’enseignement des mathématiques doit se faire selon une progression « concrète -> imagée -> abstraite », c’est-à-dire en privilégiant d’abord la manipulation (qui est ultimement au service de l’abstraction) et en offrant des représentations multiples de tout concept abordé pour aider les élèves à donner du sens aux expressions et équations mathématiques qui suivront » [20] .

Beaucoup de chercheurs insistent sur l’intérêt de disposer de plusieurs registres de représentations. Pour Duval [10] : «« La compréhension mathématique commence lorsque la coordination des registres commence. […] Les processus de pensée mathématique dépendent d’une synergie cognitive des registres de représentation »³. Il faut donc favoriser les conversions entre registres de représentation (les registres de la langue écrite, de la langue orale, de l’écriture sous forme de calcul, des représentations en barres, des représentations de Vergnaud, d’autres représentations). Un des avantages de la représentation en barres est qu’elle peut connaître une évolution du concret, en passant par le visuel, puis vers l’abstrait, comme l’illustre la figure suivante extraite d’un ouvrage de la Librairie des Écoles.

représentations : verbales (mots), concrète (objets), imagée (dessins) et abstraite (symboles).

La représentation en barres permettrait d’assurer des échanges entre élèves qui ont accès directement à l’écriture pré-algébrique ou algébrique \(4+2= ?\), et élèves qui ont encore besoin d’une représentation visuelle. Elle peut être démarrée dès la grande section maternelle avec des alignements d’objets concrets. C’est donc la pérennité de cette représentation du cycle 1 au cycle 4 qui lui donne cette importance plutôt qu’une domination : les représentations en barres pourront modéliser des problèmes additifs, des problèmes multiplicatifs, avec des fractions et des pourcentages. Bien entendu, il n’est pas question d’interdire à des élèves d’utiliser d’autres représentations, ni d’obliger un élève qui représente directement dans le registre pré-algébrique (avec des additions ou des multiplications à trou par exemple) de passer obligatoirement par une représentation en barres. Cependant, ce passage par la représentation en barres pourrait être un moyen de communiquer plus facilement avec ses camarades qui auraient des difficultés d’accès direct au registre algébrique.

On peut également critiquer le nombre limité de cas basiques (trois cas basiques dans les catégorisations de Ng-Lee ou de Kaur). C’est une grande différence par rapport à toutes les catégories que certains ont proposés par rapport à la typologie de Vergnaud [8] [12]. Cette multiplication des modèles basiques peut d’ailleurs poser un problème de mémorisation pour certains élèves. En faveur de cette limitation de problèmes basiques, nous pouvons évoquer le recodage sémantique de Sander : « l’objectif du recodage sémantique est de faire apparaître la ressemblance profonde entre deux situations qui, en dépit des différences sémantiques, sont analogues sur le plan des notions disciplinaires […] Le recodage sémantique peut également être suscité par la comparaison d’énoncés en travaillant avec les élèves à la mise en place d’un codage commun qui rend perceptible les analogies existant entre les énoncés […] De tels recodages sémantiques favorisent la perception d’analogies qui fondent les notions et peuvent favoriser un développement de la conceptualisation » .

À titre d’exemple pour les problèmes avec un axe temporel, plutôt que d’inventer de nouvelles représentations comme pour les problèmes de transformation de Vergnaud ou les représentations graphiques de Petit [24], il peut être intéressant de recoder sémantiquement ces problèmes avec un recodage sans axe temporel. Illustrons par un exemple où le problème de avant-après (ou transformation d’états) est recodé en problème parties-tout, où le tout représente l’objet après qui est la réunion de deux parties : l’objet avant et la partie correspondant à l’augmentation.

Cependant, cette simplification de la catégorisation ne doit pas faire croire que les difficultés relevées par Vergnaud ou Petit ont disparu. Elles doivent être traitées dans la discussion pour reconnaître le modèle commun aux problèmes parties-tout et avant-après. Faut-il passer par des représentations intermédiaires (du type de celles de Vergnaud et Petit) ? De même, Vergnaud propose une analyse fine des problèmes multiplicatifs, avec notamment les représentations en tableau pour la proportionnalité [17]. Est-ce que les représentations en barres peuvent répondre à cette analyse fine ? Ou se limitent-elles aux problèmes de variations (fractions et pourcentages) ? La recherche et les expérimentations en classe devront nous éclairer pour répondre à ces questions. Pour le moment, nous n’avons pas trouvé de résultats convaincants en faveur des représentations en barres alors que des résultats intéressants ont été trouvés concernant les représentations de Vergnaud [18].

On peut observer également que certains problèmes sont choisis avec les bonnes variables didactiques qui rendent la résolution aisée avec la représentation en barres.

Par exemple, le problème suivant devient plus difficile à représenter en barres en remplaçant \( {6}\) cm par \( {13}\) cm et en gardant \( {18}\)
cm pour l’arbre.

Enoncé 4
Sur la photo, Jean mesure \( {6}\) cm de haut et l’arbre mesure \( {18}\) cm. Sachant qu’en réalité Jean mesure \( {120}\) cm de haut, quelle est la hauteur réelle de l’arbre ?

De même, les problèmes de proportionnalité qui se représentent facilement dans des tableaux deviennent complexes à représenter dans des représentations en barres si le nombre de colonnes et de lignes devient important. Les problèmes avec fractions sont d’ailleurs très privilégiés dans les représentations en barres alors que dans les programmes actuels les fractions sont surtout introduites comme outil pour que les fractions décimales puissent donner sens aux nombres décimaux. Mais les fractions ne sont objets d’étude qu’au collège, au moment où l’entrée dans l’algèbre devrait être mieux assurée qu’à l’école primaire. Il ne faudrait pas que l’introduction des représentations en barres soit un prétexte pour faire des fractions un objet d’étude dès l’école primaire : sinon il serait intéressant de mesurer l’impact d’une telle modification, compte tenu des difficultés des élèves sur les contenus actuels.

Concernant les ressources relatives à la représentation en barres, remarquons encore un élément. Pour la collection de la Librairie des Écoles consacrée à la méthode de Singapour et utilisant les représentations en barres, «le dispositif didactique est le plus souvent de type “explication – application” : l’enseignant livre le savoir, les élèves l’appliquent. Il est plus rarement de type “observation – compréhension – application” […] l’enseignant montre ce qui est à faire, sans que chaque élève ait pu être confronté individuellement à une tâche de découverte. Les élèves appliquent ensuite ce qui a été expliqué dans des exercices similaires» [19]. Dans l’ouvrage intéressant, remarquablement argumenté et soumis à la discussion, de Jamet sur la résolution de problèmes en utilisant les représentations en barres, du CE2 au CM2, sont proposées des progressions abondamment illustrées par des séquences mises en œuvre en classes. Jamet y défend un temps conséquent accordé à la pratique de résolution de problèmes guidée par l’enseignant avant de passer à une pratique autonome. Dans cette pratique guidée, «cela se traduit par une grande importance accordée aux échanges avec les élèves tout au long des séances […] réflexion et analyse personnelles et travail collaboratif sont des temps préalables à l’entraînement en autonomie» [15]. On voit donc que les représentations en barres peuvent être utilisées par l’enseignant de différentes manières, cette observation étant en fait valable pour toute autre représentation et pas spécifique aux représentations en barres.

Une pratique d’enseignement qui ne laisse pas de place à la réflexion et à l’analyse personnelle de l’élève, et au travail collaboratif, risque d’être un obstacle à l’autonomie des élèves, quelle que soit le mode de représentation utilisé pour résoudre des problèmes.

La dernière critique, plus générale, concerne les risques de la transposition didactique : faire apparaître dans l’institution scolaire des tâches qui n’existent pas chez le mathématicien qui résout des problème et dont l’intérêt pour l’apprentissage des mathématiques est discutable. Par exemple on peut mettre en place un passage obligé par la représentation en barres alors qu’un élève sait s’en dispenser. Ou encore imposer un soin du tracé, l’utilisation de pochoirs, ou la proportionnalité entre longueurs barres et mesures qu’elles représentent, alors que le but est de suggérer une relation arithmétique entre mesures. Ou encore utiliser une méthodologie dénuée de sens pour résoudre des problèmes [7] [14], comme souligner dans l’énoncé les éléments utiles à la résolution du problème, alors que tant que le problème n’est pas résolu, il n’est pas toujours possible de savoir ce qui sera utile. Ou encore s’entêter à utiliser une représentation en barres dans un problème atypique qui ne relève pas de ce type de représentation. Parfois, on découpe en tâches isolées la résolution de problème, par exemple associer un énoncé à un type de schéma, ou associer des énoncés relevant d’un même modèle, ou associer un calcul à un schéma. Savoir convertir d’un registre à un autre, ou recoder sémantiquement un énoncé, évoqués précédemment, sont des compétences intéressantes mais elles ne doivent pas minorer la compétence de résolution complète d’un problème.

Conclusion

Les représentations en barres : une possibilité d’encourager les pratiques réflexives pour développer les raisonnements heuristiques et de preuve, dans un dispositif évolutif et pérenne.

Nous avons montré que les représentations en barres, comme tout autre registre de représentation, possèdent des avantages et des inconvénients. Et c’est justement parce que tous les registres ne sont pas obligatoirement congruents [10] qu’il est intéressant de savoir convertir d’un registre à l’autre. Mais nous souhaitons insister sur l’importance du travail sur la compétence «raisonner». Les élèves développent des questionnements heuristiques⁴ et des arguments pour justifier les réponses à ces questionnements. Les élèves essaient de reconnaître des problèmes basiques ou de décomposer le problème initial en problèmes basiques, en s’aidant éventuellement de représentations, en justifiant les reconnaissances et les décompositions. Si les élèves n’y arrivent pas, notamment dans le cadre de problèmes atypiques, il faudra construire un nouveau modèle, qui sera peut-être singulier au problème à résoudre. Une fois un modèle adopté, l’élève traite le modèle (pour les problèmes arithmétiques à l’aide du calcul) pour trouver une solution au problème. Ensuite, des raisonnement de preuve valident le choix du modèle et des traitements du modèle. Donc, ce qui est essentiel dans l’utilisation des représentations en barres, c’est la position réflexive de l’élève, par rapport à cette utilisation. Cette position n’est d’ailleurs pas spécifique aux représentations en barres.

Par rapport à la compétence communiquer, le schéma en barres peut être un outil de médiation entre différents registres de représentation. Un élève qui a des difficultés à comprendre un énoncé écrit, va pouvoir travailler sur une représentation en barres davantage visuelle que l’énoncé écrit. Dans le registre de la langue orale, les justifications, basées sur cette représentation en barre, permettront de traduire les relations arithmétiques entre nombres dans le registre préalgébrique, avec l’écriture d’un calcul entre nombres, parmi lesquels un nombre sera inconnu. Le schéma en barre peut donc apparaître comme un registre de représentation pouvant aider au passage du registre de l’écrit en langue naturelle au registre préalgébrique.

Ces représentations peuvent être installées dès la grande section maternelle, à partir de manipulation, jusqu’au cycle 4 où elles facilitent l’entrée dans l’algèbre [21]. Pour mesurer l’efficacité de ces représentations, il reste à ouvrir les chantiers d’observations des pratiques [9], de témoignages [15], de la recherche [16] [19] [21] et des évaluations (DEPP, TIMSS, PISA [22]). Il est souhaitable que les choix à effectuer (règles de représentation, catégories basiques retenues, progression dans les représentations, formes écrites et orales de l’institutionnalisation, procédures et aides privilégiées) soient argumentés à partir d’analyses des pratiques ou de résultats de la recherche consistants. Les dispositifs de type groupe IREM, ou de type lesson study [13] en lien avec les référents mathématiques de circonscriptions du rapport Torossian-Villani pourraient également être d’excellents dispositifs d’étude de cette efficacité.

Références

Bloch, I. (2018). Texte pour la mission mathématique. ARDM. Au fil des maths, 528, revue numérique. APMEP.
Bosch, M., Gascón, J. (2006). 25 years of didactic transposition. ICMI Bulletin, 58, 1-2-3, 51-64.
Centre Alain Savary (2018). Catégorisation des problèmes en mathématiques., un enjeu langagier majeur. Institut Français de l’Education.
Cabassut, R. (2005) Raisonnement plausible versus raisonnement de nécessité : où est la frontière ?, in Actes du XXXIIe Colloque COPIRELEM, 17- 19 mai 2004, Foix, IREM de Toulouse, mai 2005.
Chambris, C. (2008). Relations entre les grandeurs et les nombres dans les mathématiques de l’école primaire. Évolution de l’enseignement au cours du 20e siècle. Connaissances des élèves actuels.Thèse. Université Paris-Diderot. .
Chambris, C. (2017). L’enseignement des maths à l’école et la méthode de Singapour, Bulletin de la CFEM, 44, 13 – 18. .
Coppé, S., Houdement, C. (2002). Réflexions sur les activités concernant la résolution de problèmes à l’école primaire, Grand N. 69, 53-63. .
Durpaire, J.L. (2006). L’enseignement des mathématiques au cycle 3 de l’école primaire. IGEN.Rapport – n° 2006-034. Juin 2006 Ministère de l’Education Nationale..
Durpaire, J.-L., Mégard, M. (coor.) (2008). Le nombre au cycle 2. SCEREN- NDP-CRDP d’Orléans-Tour. .
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics (2006) 61: 103–13. .
Glaeser, G. (1990). Analyse et synthèse. Formation des enseignants en heuristique. Publication de l’APMEP N° 76. .
Graff,O., Calmelet J.-J., Wozniak, V (2011). Situations multiplicatives – Problèmes de multiplication et de division. Canopé – CRDP de Lille.
Hartmann, F., Masselin, B. (2019). Ingénieries de formation en mathématiques : des réalisations inspirées des Lesson Studies. Au Fil des Maths. N° 534.
Houdement, C. (2018). Problèmes arithmétiques basiques : le cœur du problème ?, in Julia Pilet & Céline Vendeira (ed.) (2018) Préactes du séminaire de didactique des mathématiques.ARDM .
Jamet, J.-M. (2019). Résoudre les problèmes avec la modélisation du CE2 au CM2. Hachette Education.
Kaur, B. (2019). The why, what and how of the ‘Model’ method: a tool for representing and visualising relationships when solving whole number arithmetic word problems. ZDM Mathematics Education (2019) 51:151-168. .
Levain, J.P. Vergnaud, G. (1995). La proportionnalité simple et multiple. Grand N, n°56, 55- 67 .
Levain, J.P., Le Borgne, P., & Simard, A. (2006). Schématisation et résolution de problèmes en SEGPA. Revue Française de Pédagogie, 155, 95 – 105. .
Mounier, E., Grapin, N.(2019). Que disent les recherches sur les manuels « Méthode de Singapour » ? Au fil des Maths, n° 532, p.6-13..
Neagoy, M. (2017) La « méthode de Singapour » à l’école primaire. Entretien avec Monica Neagoy, propos recueillis par Jean-Michel Zakhartchouk, 4 avril 2017. .
Ng, S. F., Lee, K. (2009).The Model Method: Singapore Children’s Tool for Representing and Solving Algebraic Word Problems. Journal for Research in Mathematics Education, 2009, Vol. 40, No. 3, 282–313..
OCDE (2014). Trouver des solutions créatives : quelles sont les compétences des jeunes de 15 ans en résolution de problèmes ? PISA à la loupe – 2014/04..
Parzysz, B. (1988). Voir et savoir-la représentation du « perçu » et du « su ». Bulletin de l’APMEP, N° 364, p.339-350.
Petit, S. (2012). Problèmes additifs à transformations et représentations graphiques à l’école.Bulletin de l’APMEP. N° 500. p. 389-400..
Polya, G. (1957). How To Solve It. Princeton University Press, 1957 .
Sander, E. (2018). Une approche interprétative de la résolution de problèmes, in Julia Pilet & Céline Vendeira (ed.) (2018) Préactes du séminaire de didactique des mathématiques. ARDM..
Torossian C., Villani C. (2018). 21 mesures pour l’enseignement des mathématiques. Ministère de l’Education Nationale. France..
Vergnaud,G. (1981). L’enfant, la mathématique et la réalité. Berne : Éditions Peter Lang.
Vergnaud, G. (1989). Psychologie du développement cognitif et didactique des mathematiques un exemple: les structures additives. Petit \(x\), N° 22, pp. 51 à 69..