Des cercles sur des surfaces ?
Chacun connaît le cercle d’Euclide, bien rond, bien lisse, bien convexe, avec son centre et son rayon.
Robert Ferréol nous propose de découvrir des cercles exotiques mais cependant très proches, ayant plusieurs centres ou rayons, éventuellement tangents à eux-mêmes, voire même avec plusieurs composantes connexes.
Robert Ferréol
© APMEP Mars 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Comment définir, et réaliser, un cercle sur une surface quelconque ?
Deux définitions
Nous allons voir que les définitions du cercle auxquelles nous sommes habitués dans le plan peuvent conduire sur des surfaces dans l’espace à des réalisations distinctes !
Éliminons tout d’abord la définition du tracé avec un compas : si on plante la pointe du compas en un point de la surface, il faut déjà, pour tracer un « cercle », que la deuxième branche du compas ne traverse pas la surface ; et si c’est le cas, on obtient l’ensemble des points de la surface situés à une distance en ligne droite de la pointe ; autrement dit l’intersection d’une sphère centrée sur la surface avec cette surface. L’étude des intersections sphère-surface est certes très intéressante, mais nous aimerions nous occuper des cercles vus par des habitants de la surface qui, comme nous sur la terre, seraient suffisamment petits pour ne pas voir que leur surface est courbe…
La définition scolaire (et pas du tout naturelle chez les élèves !) du cercle est : « ensemble des points situés à même distance d’un centre ». On peut la transposer sur une surface, à condition de prendre comme distance la distance géodésique, c’est-à-dire la longueur du plus court chemin inclus dans la surface (ce chemin s’appelle une géodésique) : ce sera notre « définition 1 ». Concrètement, pour obtenir une géodésique ; on tend un fil entre deux points en l’appliquant sur la surface (mais ceci ne fonctionne que si la surface est toujours située du même côté du plan tangent, comme par exemple un ellipsoïde).
Plus mathématiquement, une géodésique est une courbe dont le plan osculateur1 contient la normale2 à la surface.
L’autre définition, qui sera plus naturelle pour les habitants de la surface, est celle d’une courbe à courbure constante (dans un véhicule parcourant la surface en bloquant le volant, on avance en tournant régulièrement vers la droite, ou la gauche). Mais quelle est la définition de cette courbure, dite « courbure géodésique », pour une courbe tracée sur une surface ?
En un point donné, ce sera l’inverse du rayon de la meilleure sphère épousant la courbe, centrée dans le plan tangent à cette courbe. Mais quelle est cette meilleure sphère ? On démontre que c’est la sphère centrée dans le plan tangent à la surface qui contient le cercle osculateur3 à la courbe. Son centre (centre de courbure géodésique) se projette donc dans le plan osculateur à la courbe en le centre de courbure (voir la figure 1).
Figure 1. Vue en coupe dans le plan perpendiculaire à la tangente en un point de la courbe. ↩
Le rayon de courbure \(R_c\) et le rayon de courbure géodésique \(R_{cg}\) (vu par les habitants de la surface) sont donc reliés par la relation \[R_{cg} = \frac{R_c}{\cos(\theta)}\] où \(\theta\) est l’angle entre le plan osculateur à la courbe et le plan tangent à la surface. En prenant les inverses, la courbure \(\gamma\) et la courbure géodésique \(\gamma_g\) sont reliées par \(\gamma_g = \gamma \cos(\theta)\). Prenons un exemple extrême : l’équateur de la terre (ou plus généralement d’un grand cercle d’une sphère). Le cercle osculateur à l’équateur est l’équateur lui-même. Les habitants de l’équateur ont un plan tangent (à la sphère terre) qui est perpendiculaire au plan de l’équateur, donc \(\theta = \dfrac{\pi}{2}\) et ils voient donc l’équateur avec une courbure nulle ; la courbure réelle de l’équateur est non nulle (c’est l’inverse du rayon de la terre), mais sa courbure géodésique est nulle ; d’ailleurs si une route suit l’équateur, ne sera-t-elle pas rectiligne ?
La sphère
Commençons justement par la sphère. C’est le seul cas où les cercles géodésiques sont des cercles « normaux » ; mais on va voir qu’ils ont \(4\) rayons possibles ! Considérons le cercle parallèle de colatitude \(\theta\) d’une sphère de rayon \(a\) (voir la figure 2) ; en tant que cercle « normal » il a pour rayon \(a \sin(\theta)\). Avec la définition 1, il a deux centres, les pôles nord et sud \(N\) et \(S\), et donc deux rayons \(a\theta\) et \(a(\pi – \theta)\). Avec la définition 2, son centre \(\Omega\) est le point du plan tangent à la sphère en un point \(M\) du cercle qui se projette sur le plan du cercle au centre « normal » de ce cercle, et son rayon est donc \(a \tan(\theta)\).
Figure 2. Cas de la sphère. ↩
L’équateur, qui a \(a\) pour rayon habituel, a donc \(\dfrac{\pi}{2}a \) pour rayon avec la définition 1, et \(\infty\) avec la définition 2 (c’est une géodésique, comme on l’a vu plus haut).
Les cylindres
Une catégorie de surfaces où les cercles géodésiques sont faciles à déterminer est formée par les cylindres, pas seulement de révolution. Si vous prenez une feuille de papier cartonné rectangulaire où est tracé un cercle, la posez verticalement sur une table, et forcez la base à suivre une courbe donnée, le cercle courbé tracé sur la feuille sera un cercle géodésique de la feuille-cylindre. Simple à faire avec du carton, moins simple mathématiquement !
Pour que les distances soient conservées dans le cylindre, il faut paramétrer la courbe de base par son abscisse curviligne \[\begin{cases}
x &= f(s) \\
y &= g(s)
\end{cases}\] et dans le cylindre \[\begin{cases}
x & = f(s) \\
y & = g(s) \\
z & = z
\end{cases}\] les points sont repérés par leurs coordonnées dites « géodésiques » \(s\) et \(z\). Pour obtenir un cercle géodésique de centre \((0\, ;\,0\, ;\,0)\) et de rayon \(r\), il suffit de poser \(s = r \cos(\theta)\), \(z = r \sin (\theta)\), d’où la paramétrisation de ce cercle (\(r\) fixé, \(theta\) variable) :
\[\label{eq :1}
\begin{cases}
x &= f (r \cos(\theta))\\
y &= g (r \cos(\theta))\\
z &= r \sin(\theta)
\end{cases}\]
Par exemple, pour le cylindre de révolution de rayon \(a\), on a \(f(s)=a\cos\left(\dfrac{s}{a}\right)\), \(g(s)=a\sin\left(\dfrac{s}{a}\right)\) d’où la paramétrisation du cercle géodésique :
\[\begin{cases}
x &= a \cos \left(\dfrac{r}{a}\cos(\theta)\right)\\
y &= a \sin \left(\dfrac{r}{a}\cos(\theta)\right)\\
z &= r \sin(\theta)
\end{cases}\]
La figure 3 a été obtenue en demandant à de tracer la surface paramétrée en \(u\) et \(v\) :
\[\begin{cases}
x &= \cos \left(u\cos(v)\right)\\
y &= \sin \left(u\cos(v)\right)\\
z &= u\sin(v)
\end{cases}\]
en faisant apparaître les lignes obtenues à \(u\) et \(v\) constants. On voit alors bien apparaître les cercles géodésiques centrés en \(O\) ainsi que les géodésiques issues de \(O\).


Figure 3. Cercles géodésiques, et géodésiques issues du centre. ↩
Dès que le diamètre du cercle géodésique est supérieur à la circonférence du cylindre, le « cercle » se recoupe lui-même, et arrive même un moment où il passe par son centre (figure 4) !
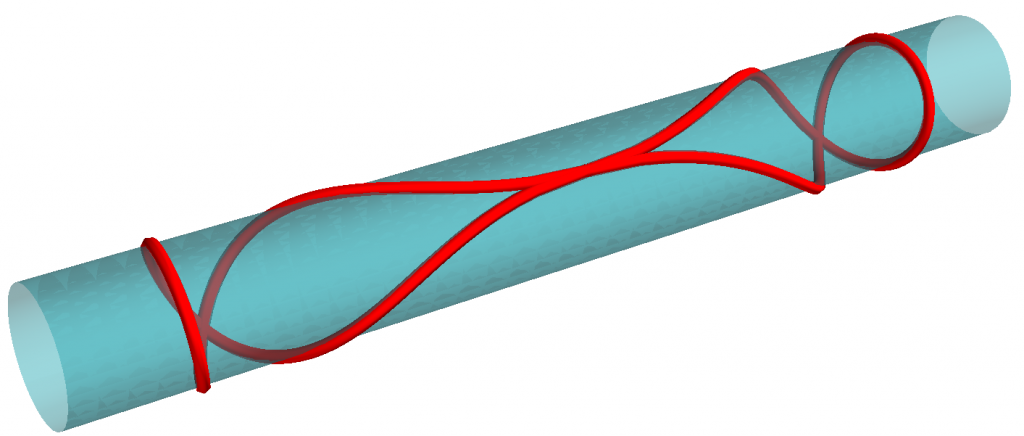
Figure 4. Cercle géodésique sur un cylindre. ↩
Malheureusement peu de courbes ont une abscisse curviligne qui se calcule à l’aide des fonctions usuelles… J’aurais aimé tracer des cercles sur un cylindre de base une sinusoïde, mais comme son abscisse curviligne n’est pas sympathique, vous aurez droit à un cylindre de base une arche de cycloïde (figure 5).
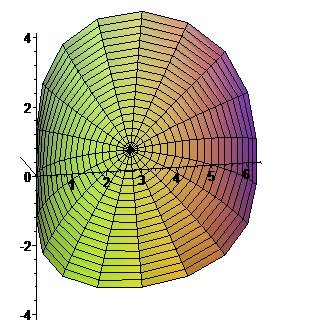
Figure 5. Cercle géodésique sur un cylindre de base une arche de cycloïde. ↩
Tous calculs faits, la surface est paramétrée en \(u\) et \(v\) par : \[\begin{cases}
x &= \arccos( u \cos v) – u \cos \left(v \sqrt{1 – u^2 \cos^2 v}\right) \\
y &= 1 – u^2 \cos^2 v \\
z &= 2u \sin v
\end{cases}\]
Les surfaces développables
Les cylindres, avec les cônes, sont des cas particuliers de surfaces dites « développables », des surfaces réglées4 telles que le plan tangent est toujours le même le long d’une génératrice.
Lorsqu’on les pose sur un plan, elles peuvent rouler sans glisser sur ce plan, et les cercles géodésiques (par la définition 1 ou la définition 2) sont les courbes dont la trace sur le plan est un cercle habituel.
Voici la paramétrisation du cercle géodésique de rayon \(r\), de centre situé à une distance \(a\) du sommet d’un cône de demi-angle au sommet \(\alpha\) (variable \(t\)) :
\[\begin{cases}
x &= \left|a+ r\text{e}^{\text{i} t}\right| \sin (\alpha) \cos
\left(\dfrac{\arg(a+r\text{e}^{\text{i} t})}{\sin(\alpha)}\right) \\
y &= \left|a+ r\text{e}^{\text{i} t}\right| \sin (\alpha) \sin
\left(\dfrac{\arg(a+r\text{e}^{\text{i} t})}{\sin(\alpha)}\right) \\
z &= \left|a+ r\text{e}^{\text{i} t}\right| \cos (\alpha)
\end{cases} ;\] la figure 6 a été tracée par Alain Esculier à partir de cette formule à l’aide du logiciel .

Figure 6. Cercles sur un cône. ↩
Mais vous pouvez courber une feuille de papier cartonné (sans pli) de sorte qu’elle ne soit ni un cylindre, ni un cône. Les cercles que vous aurez tracés au préalable seront des cercles géodésiques de cette surface développable.
C’est ce que j’ai fait avec ces dessous d’assiettes rapportés du Mexique (figure 7) !

Figure 7. ↩
Dans les exemples précédents, on sous-entendait l’existence d’un plan tangent en tout point. Mais on peut aussi tracer des cercles sur des polyèdres. Pour des cercles de rayon pas trop grand, on peut développer l’un de leurs patrons, tracer un cercle et reconstituer le polyèdre. Voici par exemple, des cercles géodésiques centrés au sommet d’un cube dont on remarque qu’ils ont une longueur égale au \(\dfrac{3}{4}\) de leur longueur habituelle, en tous cas tant que le rayon est inférieur au côté du cube (figure 8).
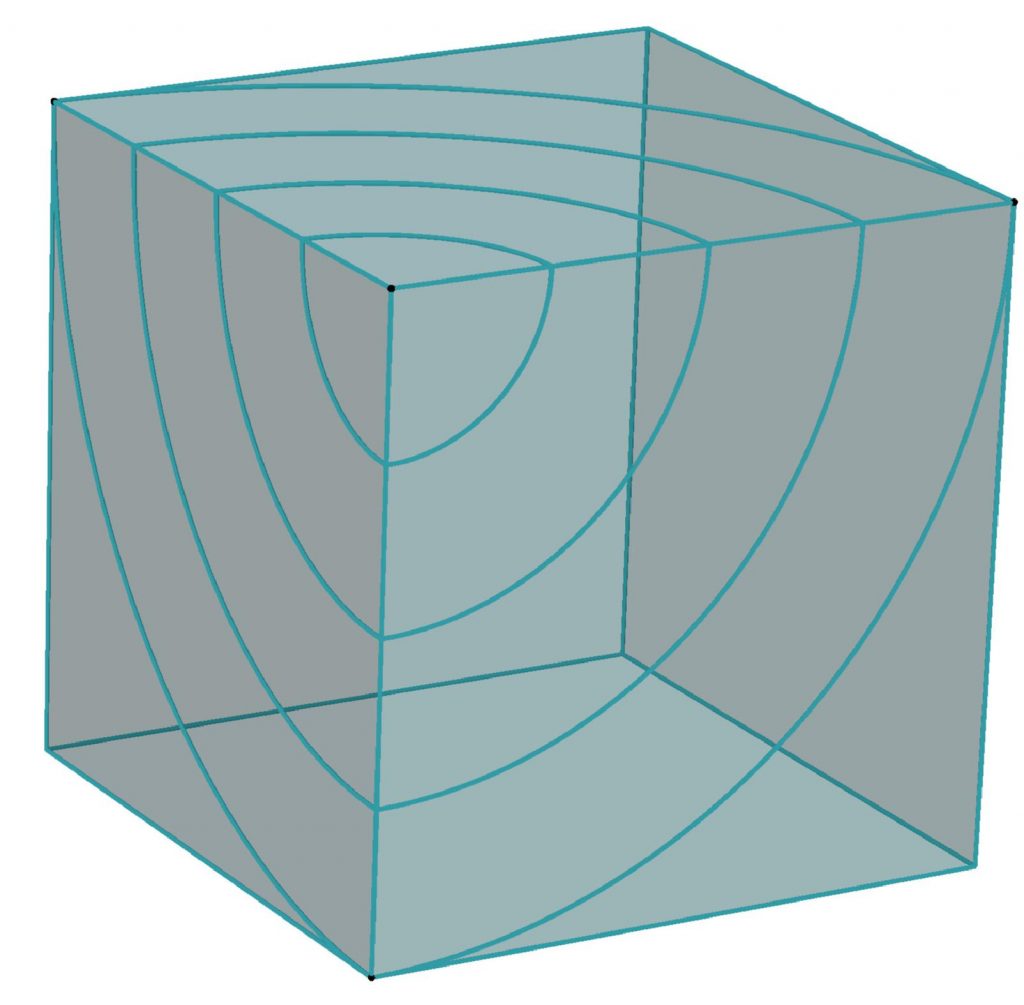
Figure 8. Cercles sur un cube. ↩
Pour des cercles de rayons plus grands ou centrés en un point quelconque du cube, cela se complique nettement avec des possibilités de « cercles » de même centre qui se croisent ou qui ne se ferment pas. Si des lecteurs veulent étudier la question, il y aura une synthèse des résultats dans le prochain numéro…
Les surfaces à courbure totale constante
Quelques points théoriques :
-
D’après le théorème dit « de Meusnier », les surfaces présentent en chaque point deux cercles de courbure5 principaux orthogonaux indiquant chacun les extremums \(\gamma_1\) et \(\gamma_2\) de la courbure des sections normales de la surface. La courbure totale (ou de Gauss) est alors le produit \(\gamma_1 \gamma_2\).
-
Une surface est dite applicable sur une autre si pour tout point de la première il existe une bijection d’un voisinage de ce point (dans la surface) sur une partie de la deuxième qui conserve la distance géodésique.
-
Beltrami a montré en 1868 que les surfaces à courbure totale constante donnée sont applicables entre elles (et en particulier à une sphère si la courbure est strictement positive, à une pseudo-sphère (voir plus loin) si elle est strictement négative, et à un plan si elle est nulle).
-
Whittemore a démontré en 1901 que les deux définitions des cercles géodésiques coïncident pour les surfaces à courbure totale constante.
On en déduit que les cercles géodésiques des surfaces à courbure totale constante sont les courbes qui deviennent des cercles classiques quand on applique la surface à :
-
un plan quand la courbure totale est nulle (surfaces développables déjà considérées) ;
-
une sphère de rayon \(R\) quand la courbure totale est \(\dfrac{1}{R^2}\) ;
-
une pseudo-sphère de pseudo-rayon \(R\) quand la courbure totale est \(-\dfrac{1}{R^2}\cdotp\)
La pseudo-sphère a été définie par Beltrami en 1868 dans sa recherche d’une surface à courbure totale constante négative simple : c’est en effet la seule surface de révolution à courbure totale constante négative dont la paramétrisation fait intervenir les fonctions usuelles. Voir plus de détails sur ![]() .
.
Voici une figure qui a été réalisée par Yves Martin à l’aide du logiciel , montrant un triangle formé de segments de géodésiques (en bleu), avec son cercle circonscrit (en rouge), tracés sur la pseudo-sphère (figure 9 ; ![]() ).
).
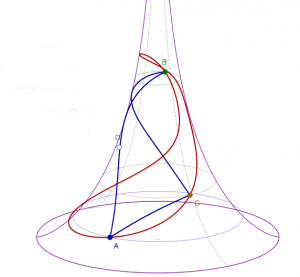
Figure 9. Vue en coupe dans le plan perpendiculaire à la tangente en un point de la courbe. ↩
Contre-exemples à l’équivalence des définitions 1 et 2
Considérons la fonction \(f\) définie par : \[f(x\, ;\,y) = \left((x-1)^2+y^2 -1\right)\left((x+1)^2 + y^2-1\right) ;\] on aura compris qu’elle a été définie pour que la surface associée d’équation \(z = f (x\, ;\,y)\) contienne dans le plan \(z = 0\) les deux cercles horizontaux de centre \(( \pm 1\, ;\ 0\, ;\,0)\) et de rayon \(1\) (figure 10). Attention, un seul cercle n’aurait pas fourni de contre-exemple, car les cercles parallèles d’une surface de révolution sont bien des cercles géodésiques…
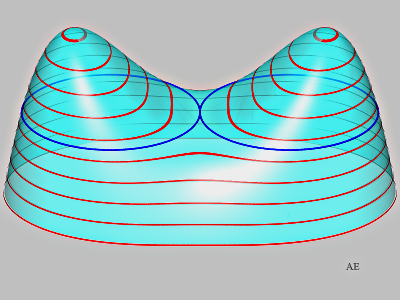
Figure 10. Les cercles sont en bleu, les lignes rouges sont
des lignes de niveau. ↩
Ces deux cercles ont une courbure constante (par définition !) mais n’ont pas une courbure géodésique constante puisque le plan tangent ne fait pas un angle constant avec le plan des cercles (visuellement, et par le calcul) : la définition 2 n’est donc pas vérifiée.
Visuellement la définition 1 n’est pas vérifiée, mais Robert March l’a montré par la méthode suivante. Il a modélisé la surface avec le logiciel et tracé la section du mamelon par le plan de symétrie ; cette section est une géodésique et si le cercle vérifiait la définition 1, son « centre » serait au milieu de cette géodésique. Il a donc tracé les géodésiques issues de ce point, et a vérifié qu’elles n’étaient pas de longueur constante (figure 11).
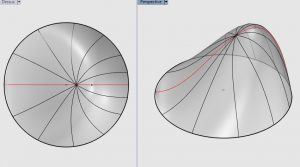
Figure 11. ↩
Donc déjà, un cercle n’a aucune raison d’être un cercle géodésique.
Maintenant, élevons la fonction \(f\) au carré de sorte que le plan tangent soit horizontal le long des cercles (figure 12).
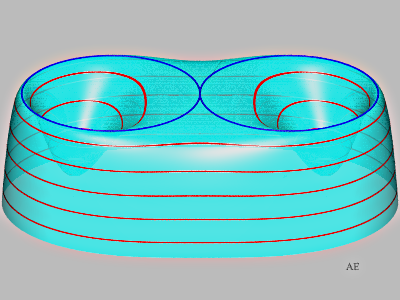
Figure 12. ↩
Le plan tangent fait cette fois un angle constant (nul) avec le plan des cercles, donc ce sont des cercles géodésiques pour la définition 2, et de la même façon que plus haut, pas pour la définition 1\(\ldots
\) Le contre-exemple où la définition 1 est réalisée et non la 2 nous sera donné par le paraboloïde hyperbolique équilatère \(z = xy\). Sont tracées sur les figures 13 et 14, les géodésiques issues de \(O\) et les points à distance géodésique données de \(O\), figurant les cercles géodésiques de la définition 1.
On constate par le calcul que la courbure géodésique n’est pas constante le long de ces « cercles », et que donc la définition 2 n’est pas réalisée.
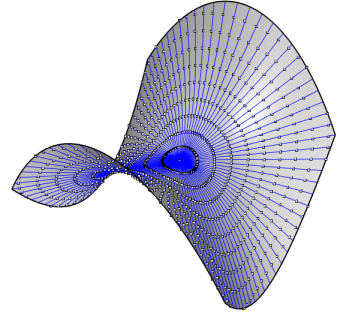
Figure 13. Vue en perspective du paraboloïde hyperbolique avec les géodésiques issues du col, et des points à distance géodésique donnée depuis le col. Cela visualise des cercles géodésiques pour la définition 1 mais pas la 2. ↩
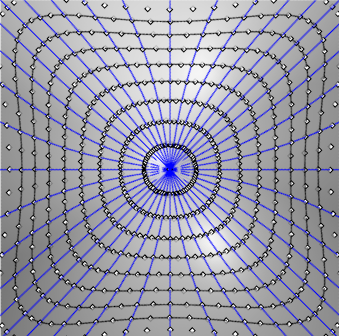
Figure 14. ↩
D’ailleurs, en relisant la démonstration de Whittemore, je me suis persuadé que la condition de constance de la courbure totale est une condition nécessaire et suffisante pour qu’on ait l’équivalence entre les définitions 1 et 2. Les surfaces à courbure constante étant en fait assez rares, on peut dire qu’en général, sur une surface quelconque, si on avance en bifurquant à gauche ou à droite d’un angle constant, il n’existera pas forcément un point situé à distance (géodésique) constante durant notre parcours. Ou qu’inversement si on trace une courbe en tendant un fil planté en un point fixe, la courbure (géodésique) ne sera pas constante…
Voir aussi les notations sur les surfaces sur le site mathcurve ![]() .
.
Références
- Georges Valiron. Équations fonctionnelles et applications. Paris : Masson, 1950.
- J. K. Whittemore. « A Note on Geodesic Circles ». In : Annals of Mathematics 3.1/4 (1901).
 , p. 21-24.
, p. 21-24.
- Wikipédia. Cercle osculateur.
 .
. - Wikipédia. Courbes gauches.
 .
. - Wikipédia. Plan osculateur.
 .
. - Wikipédia. Repère de Frénet.
 .
.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Robert Ferréol est un jeune retraité, ayant enseigné les mathématiques en CPGE, passionné de géométrie et lauréat du prix Anatole Decerf en 2008 pour son site sur les courbes et les surfaces remarquables
mathcurve.com.
-
Plan osculateur à une courbe dans l’espace : limite, lorsque \(t\) tend vers \(t_0\), du plan \(P(t\, ;\,t_0)\) passant par le point de paramètre \(t\) et contenant la tangente à la courbe en \(t_0\) ; intuitivement c’est le meilleur plan épousant la courbe. Cinématiquement, il est défini par le vecteur vitesse et le vecteur accélération.↩
-
Normale en un point d’une surface : droite perpendiculaire au plan tangent passant par le point.↩
-
Cercle osculateur (ou « de courbure ») à une courbe de l’espace en un point de paramètre \(t_0\) : limite, lorsque \(t\) tend vers \(t_0\), du cercle passant par les points de paramètre \(t\) et \(t_0\) et tangent à la courbe en \(t_0\) (cercle situé dans le plan \(P(t\, ;\,t_0 )\) ci-dessus) ; inclus dans le plan osculateur, c’est intuitivement le meilleur cercle épousant la courbe. Son rayon est le rayon de courbure, et l’inverse de ce rayon, la courbure.↩
-
Surface réglée : qui est réunion de droites (les génératrices).↩
-
Cercles de courbure en un point d’une surface : cercles de courbure des sections de la surface par des plans contenant la normale à la surface. La normale étant orientée, leur rayon peut être positif ou négatif, et les courbures correspondantes également.↩

