Au fil des problèmes n° 531
Solutions

Frédéric de Ligt

© APMEP Septembre 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

531-1 Et le triangle équilatéral

En 1978, A. Duijvestijn a découvert un découpage du carré en \(21\) carrés plus petits, tous de tailles différentes (illustration ci-contre où chaque nombre indique la longueur du côté du carré). Il a été démontré depuis que \(21\) est un record indépassable. Plus modestement, est-il possible de partager un triangle équilatéral en triangles équilatéraux plus petits, tous de tailles différentes ?

531-2 Au purgatoire des échecs

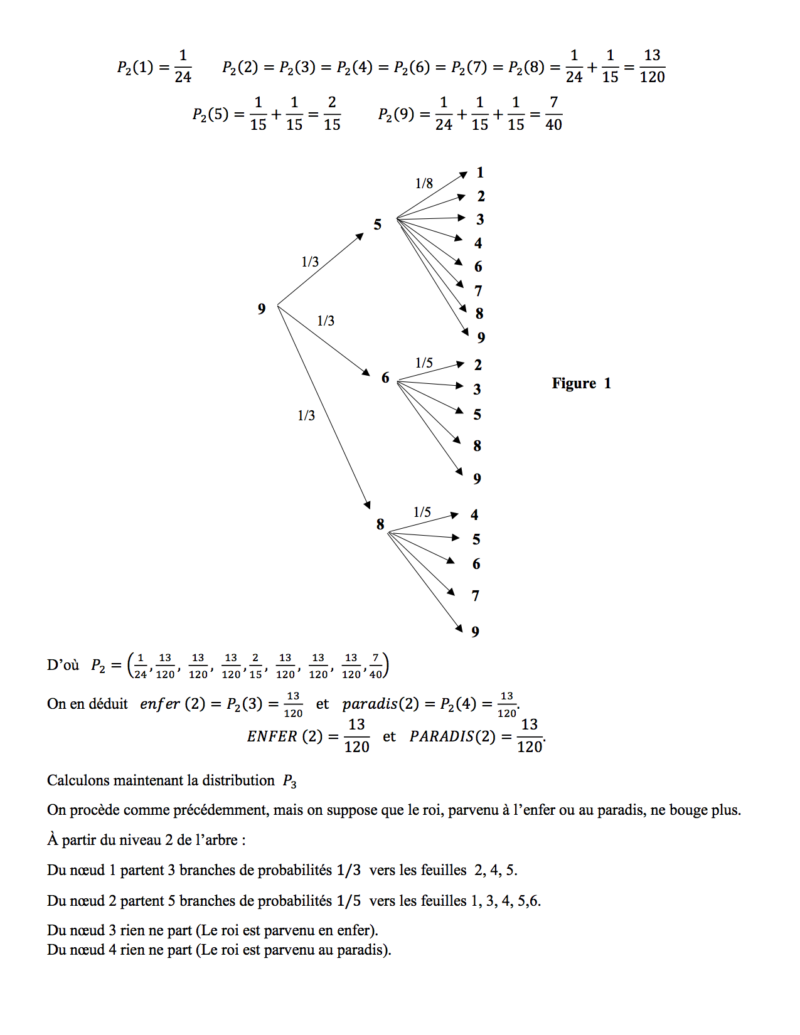
La partie est perdue. Le roi (R) est mort. Il entre maintenant dans le purgatoire des échecs. C’est un endroit qui ressemble à un petit échiquier \(3\times3\). Il y a dessus trois cases particulières: l’entrée du purgatoire où se trouve actuellement le roi, la porte (P) toujours ouverte du paradis blanc et le trou noir de l’enfer (E). Le roi va désormais errer en aveugle d’une case à l’autre, selon sa marche habituelle, en espérant que la chance lui sourira. Est-il plus probable que le roi atteigne le paradis ou qu’il tombe en enfer ?

531-3 \(\,\times\,=\,+\text{ }\)

En additionnant les prix de deux articles (en euro et au centime près), un commerçant a appuyé par erreur sur la touche \(\times\) au lieu de la touche \(+\).
Il a recommencé son calcul. Oh surprise! Il a obtenu exactement le même montant qu’auparavant.
Quels peuvent être les prix possibles de ces deux articles ?

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅