Au fil des problèmes n° 534
Solutions

Frédéric de Ligt

© APMEP Juin 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

534-1 Pour les algorithmophiles (Jean-Christophe Berthonnaud – Angoulême)

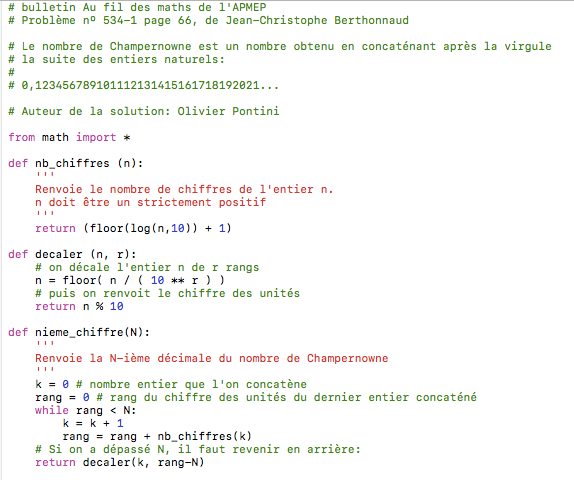
Le nombre de Champernowne est un nombre obtenu en concaténant après la virgule la suite des entiers naturels :

\[
{0,1}234567891011121314151617181920\ldots
\]

C’est un nombre univers puisqu’il est toujours possible d’y trouver n’importe quelle séquence finie de chiffres comme son numéro de sécurité sociale, son numéro de téléphone, le numéro inscrit sur sa carte bancaire, …
Il s’agit de construire un algorithme qui donne la \(n\)-ième décimale de ce nombre, et pourquoi pas ensuite de le programmer en Python.

534-2 One-to-one ? (Michel Lafond – Dijon)

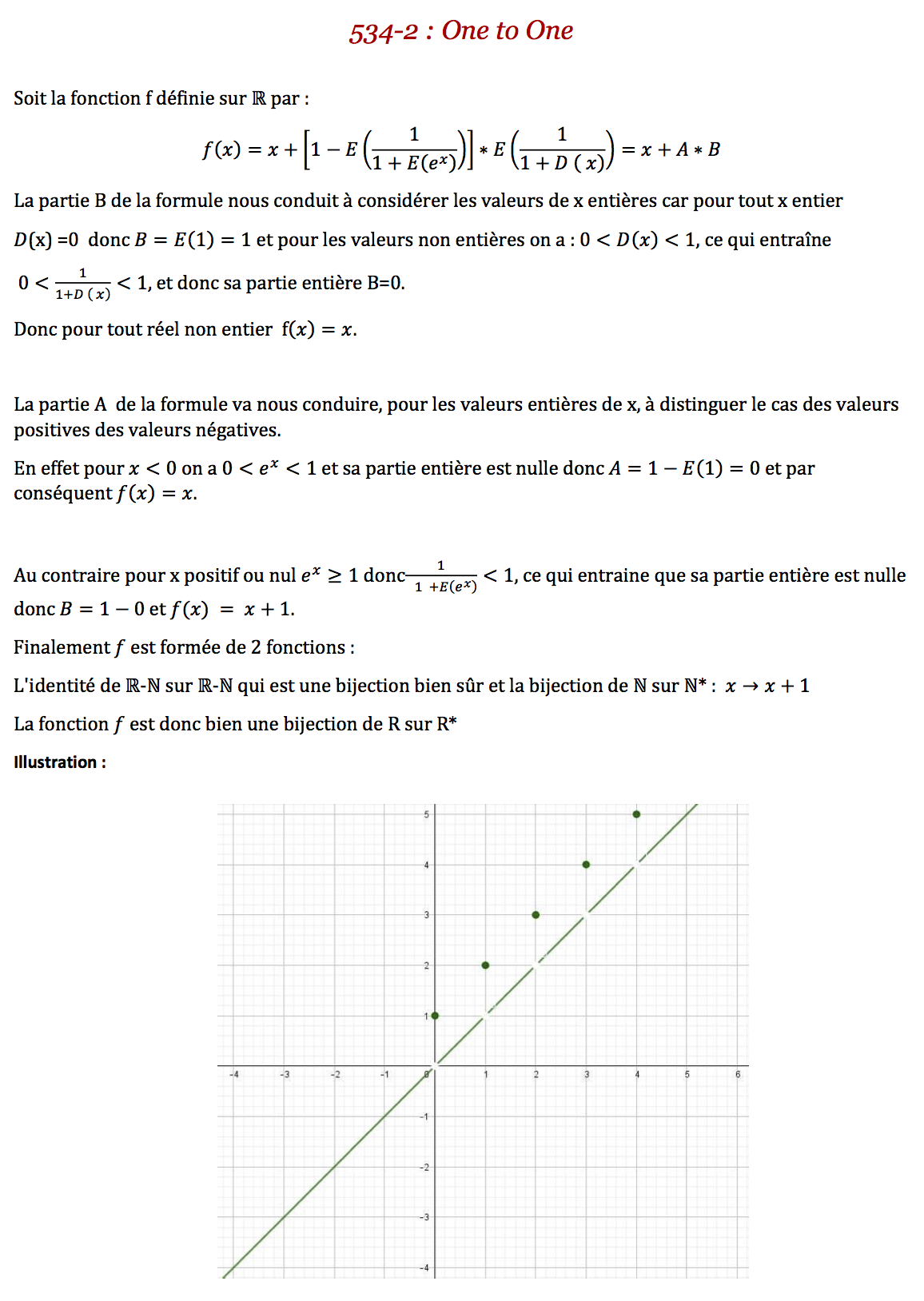
Démontrer que, pour \(x\) réel, si \(\mathrm{E}(x)\), \(\mathrm{D}(x)\), \(\text{e}^x\) désignent respectivement la partie entière de \(x\), la partie décimale de \(x\) et l’exponentielle de \(x\) alors

\[f\ :\ x\longmapsto x + \left[1-\mathrm{E}\left(\dfrac{1}{1+\mathrm{E}(\text{e}^x)}\right)\right]\times\mathrm{E}\left(\dfrac{1}{1+\mathrm{D}(x)}\right)\]

définit une bijection de \(\mathbb{R}\) sur \(\mathbb{R}^*\).

534-3 De bien des façons bis (Denis Roussillat – Vénissieux)

Il s’agit de trouver des méthodes, de niveau collège jusqu’à licence, pour montrer que, si \(a\), \(b\) et \(c\) sont trois nombres réels, \(a^2 + b^2
+ c^2 = ab + bc + ca\) si et seulement si \(a=b=c\).

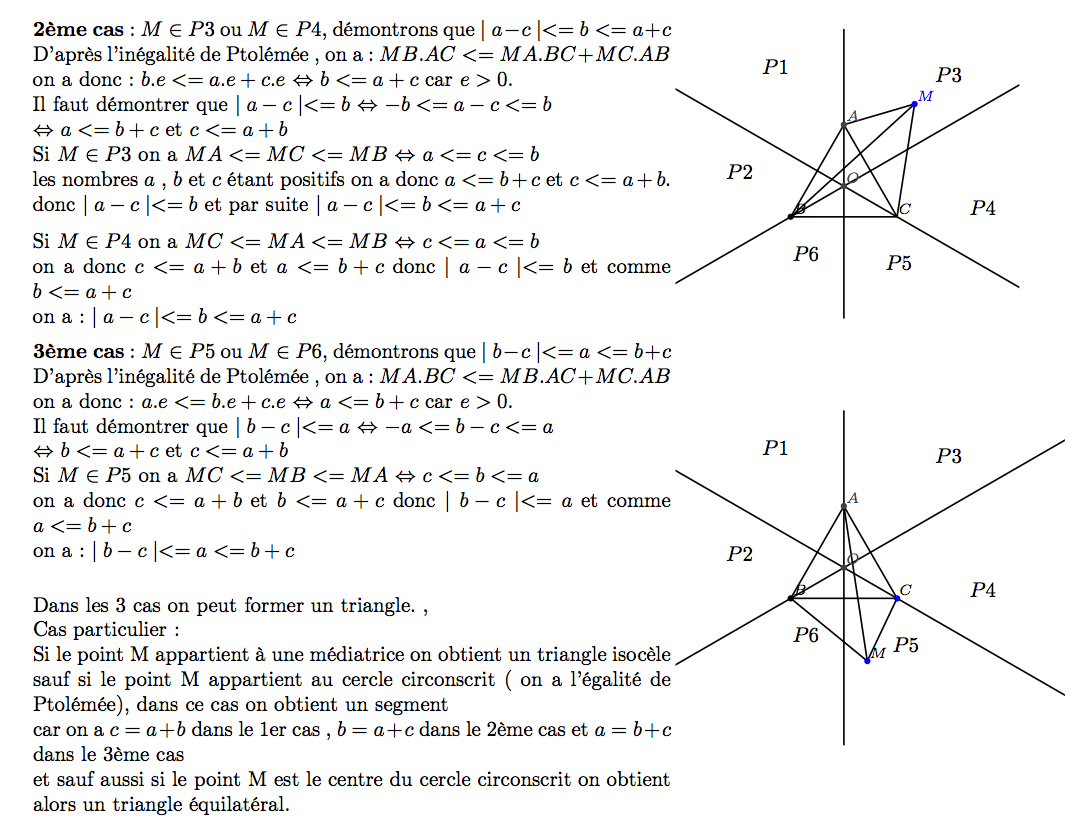
534-4 Encore une propriété du triangle équilatéral

Avec les trois segments obtenus en reliant un point quelconque du plan aux sommets d’un triangle équilatéral, on peut toujours former un triangle (éventuellement réduit à un segment).