La multiplication : découvertes en DNL
Au lycée, les sections européennes ont comme objectif de renforcer les compétences linguistiques des élèves par une utilisation transdisciplinaire de la langue étrangère tout en se familiarisant avec la culture des pays où cette langue est parlée.
Anne Reyssat partage ici quelques activités mises en œuvre en classe autour de la multiplication et des techniques opératoires.
Anne Reyssat
© APMEP Mars 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Entre 2010 et 2017, j’ai enseigné avec grand plaisir les mathématiques en langue anglaise en section européenne, de la seconde à la terminale. Comme les élèves suivent une option facultative, il s’agit de les intéresser en proposant des problèmes surprenants ou amusants, en résolvant des énigmes, en découvrant des méthodes qu’on n’utilise pas forcément en France. On développe ainsi la culture mathématique, y compris éventuellement du point de vue historique. Une autre finalité de cet enseignement est évidemment d’amener les élèves à s’exprimer en anglais (surtout à l’oral). Ainsi, le choix de situations mathématiques abordables par tous et propices à la discussion orale est essentiel.
Un exemple : une simple soustraction à retenue n’est pas toujours posée de la même façon en France et en pays anglo-saxon .
Pour 135 − 27 (“135 take away 27”) le même problème se pose à tous : on ne peut pas calculer 5 − 7 en restant dans le cadre des entiers naturels mais il n’est pas résolu exactement de la même façon.
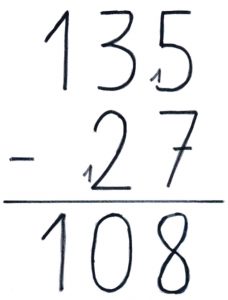
French style.
On choisit d’ajouter 10 au premier terme et de considérer 15 unités. Pour ne pas changer la différence, on ajoute aussi 10 unités (soit 1 dizaine) au deuxième terme (en anglais, “the number you’re taking away”).
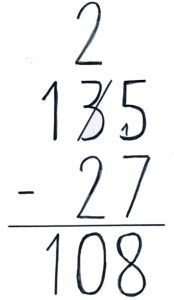
Anglo-Saxon style.
Ici, seul le nombre 135 (“the number you are taking from”) est manipulé. On emprunte (en anglais “to borrow”) une des dizaines de sorte qu’il ne reste que 2 dizaines au lieu de 3, et on ajoute cette dizaine empruntée aux 5 unités pour pouvoir soustraire 15 − 7.
Pour en savoir plus, et voir comment faire si jamais le chiffre des dizaines est un 0, vous pouvez regarder la vidéo “Multi-digit subtraction” ![]() .
.
D’une manière générale, je trouve l’utilisation de films très pertinente en cours de DNL, depuis des vidéos très courtes et très scolaires où il s’agit surtout que les élèves entendent le vocabulaire spécifique prononcé par une personne native, jusqu’à de véritables œuvres cinématographiques où on entend un très bel anglais (britannique ou non) et où on découvre un contexte culturel et un travail artistique.
Lorsque j’ai organisé des sorties au cinéma local (pour voir Comment j’ai détesté les maths, Imitation Game et The man who knew infinity), j’ai observé que les élèves appréciaient de découvrir que les mathématiques puissent donner lieu à une sortie culturelle, et qu’ils prenaient conscience que les enseignants de mathématiques étaient capables de s’intéresser à autre chose qu’à leurs équations ! L’exploitation de ces films en classe a été riche dans les trois cas.
En classe de seconde
En dehors des chiffres et des nombres entiers, les élèves qui débutent la DNL connaissent peu de vocabulaire anglais dans le domaine numérique. Donc, après quelques jeux pour apprendre à dire les nombres décimaux et les signes opératoires, je commence par faire découvrir que les opérations ne sont pas toujours effectuées comme chez nous.
Pour la multiplication, nous partons du problème simple : « si 234 autocars contiennent chacun 52 passagers, combien y a-t-il de passagers en tout ? » avec la consigne de ne pas utiliser la calculatrice et de chercher des méthodes utilisant un tableau.
Bien sûr, la première réaction est de poser l’opération et on apprend alors que « Je retiens un » se dit “I carry 1”.
Avec un peu d’imagination, les élèves inventent le tableau de gauche, remplissent les cases avec les produits 200 × 50 etc., puis additionnent plus ou moins de tête le contenu des cases. C’est une bonne occasion de dire quelques grands nombres en anglais, et surtout de se rendre compte que l’on sait effectuer ces opérations sans calculatrice et expliquer en anglais comment on procède : “I know that 2 times 5 is 10, then I add the three zeroes from 200 and 50 and I get ”.
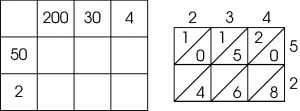
En général, les élèves ne connaissent pas la méthode per gelosia et c’est donc moi qui leur propose la grille de droite, avec la consigne de commencer par la décrire, expliquer comment les cases triangulaires ont été remplies et chercher comment l’utiliser pour retrouver le résultat de la multiplication. Après quelques hauts cris ( « c’est trop dur » ), des élèves observent où se trouvent les nombres 234 et 52, puis comprennent comment les cases triangulaires ont été remplies (“units in the bottom left triangle, tens in the top right triangle”) et enfin découvrent comment en déduire le produit 234 × 52.
Dans mon expérience, les élèves de seconde sont surtout ravis de maîtriser cette nouvelle méthode “how does it work?” et une partie d’entre eux (au moins la moitié, je le crains) se contente d’une intuition sur la place des unités, dizaines, centaines en première, deuxième et troisième diagonales et n’a aucune envie de se poser plus de questions: “why does it work ? ”. Aucune preuve générale n’a été abordée en classe. Cependant, les esprits plus curieux comprennent que, quand on effectue 4 × 5 = 20, on veut dire que 4 × 50 = 200, donc 2 centaines et 0 dizaine, d’où la place du 2 en troisième diagonale. De même 3 × 2 = 6 se réfère au fait que 30 × 2 = 60 donc 6 dizaines en deuxième diagonale et 0 centaine en troisième diagonale. C’est une des situations où j’ai eu l’impression que l’obstacle de la langue empêchait la compréhension et où j’ai parfois donné une explication en français avant de revenir à l’anglais.
L’activité se termine par un temps où la consigne est d’inventer, par groupes de quatre élèves, un problème concret conduisant à une multiplication dont les facteurs contiennent au moins deux chiffres, puis l’exposer à leurs camarades. C’est un élève extérieur à chaque groupe qui doit ensuite effectuer la multiplication avec la méthode per gelosia et exprimer la conclusion en termes concrets. J’essaie d’obtenir qu’un maximum d’élèves prennent la parole grâce à cette activité finale.
Pour faire le lien avec l’algèbre, j’utilise une vidéo très scolaire ![]() où on multiplie 43 × 21 en développant (40 + 3)(20 + 1), ce qu’on appelle en anglais “the FOIL method”. Dans la vie courante, “foil” est une feuille pour envelopper, typiquement “aluminium foil”.
où on multiplie 43 × 21 en développant (40 + 3)(20 + 1), ce qu’on appelle en anglais “the FOIL method”. Dans la vie courante, “foil” est une feuille pour envelopper, typiquement “aluminium foil”.
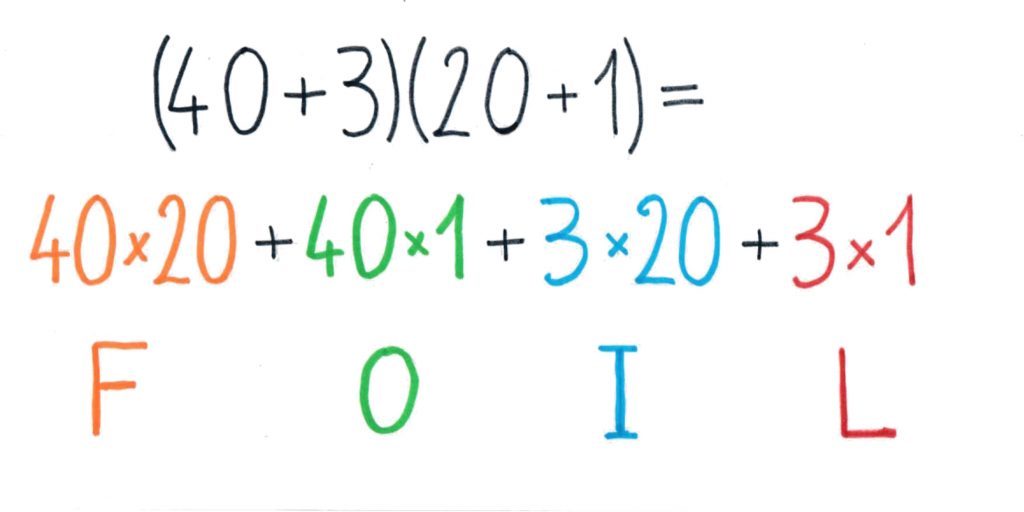
Les initiales désignent les termes à multiplier: F pour “first terms” (les premiers de chaque parenthèse) ; O pour “outside terms” (extérieurs) ; I pour “inside terms” (intérieurs) ; L pour “last terms” (les derniers de chaque parenthèse). On abrège parfois en disant “firsts, outers, inners and lasts”. Bien sûr le calcul avec l’utilisation des zéros est exactement le même qu’avec le premier tableau ci-dessus. Mais on trouve là un bon rappel et un moyen mnémotechnique pour la manière de développer le produit de deux binômes.
Enfin, pour conclure avec une touche humoristique, j’ai pu utiliser l’an dernier le sketch “7 into 28” ![]() d’Abbott et Costello (duo de comiques américains des années 1940-1950) où Costello « prouve » de trois façons fallacieuses que 7 × 13 = 28 par division, multiplication et addition. Si les élèves sont d’abord déconcertés, ils comprennent rapidement que ce n’est pas sérieux et prennent grand plaisir à rejouer le sketch à leurs camarades. On explique ensuite les erreurs commises dans un temps dialogué : il s’agit essentiellement de confusions entre dizaines et unités. En divisant 28 par 7, l’erreur consiste à diviser d’abord le chiffre des unités 8 par 7 et à porter le résultat comme chiffre des dizaines du quotient !
d’Abbott et Costello (duo de comiques américains des années 1940-1950) où Costello « prouve » de trois façons fallacieuses que 7 × 13 = 28 par division, multiplication et addition. Si les élèves sont d’abord déconcertés, ils comprennent rapidement que ce n’est pas sérieux et prennent grand plaisir à rejouer le sketch à leurs camarades. On explique ensuite les erreurs commises dans un temps dialogué : il s’agit essentiellement de confusions entre dizaines et unités. En divisant 28 par 7, l’erreur consiste à diviser d’abord le chiffre des unités 8 par 7 et à porter le résultat comme chiffre des dizaines du quotient !
Dans la multiplication, le résultat de 7 × 1 est considéré comme une unité au lieu d’une dizaine.
Enfin, Costello additionne 13 + 13 + 13 + 13 + 13 + 13 + 13 de la façon suivante. D’abord les unités : trois, six, neuf, douze, quinze, dix-huit, vingt-et-un; puis les dizaines : vingt-deux, vingt-trois, vingt-quatre, vingt-cinq, vingt-six, vingt-sept, vingt-huit !
L’opération de division aussi se prête à des découvertes et à des descriptions en anglais. Par exemple, divisons 68 par 5 :
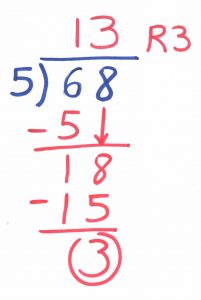
“I put the smaller number (the divisor) on the left ; then next to it, I draw a circular arc like a closing bracket ; then, on the same line, I write the larger number (the dividend) on the right and I draw a horizontal line on top of that last number. The successive subtractions will go beneath the dividend and the result will be written above the dividend”. Remarquez que le résultat se compose de deux nombres : le quotient et le reste !
En classe de terminale : la multiplication éthiopienne
Une de mes activités à succès en terminale consiste à présenter et comprendre des tours de « magie » à explication mathématique, que les élèves prennent toujours grand plaisir à jouer eux-mêmes et qui leur donnent une bonne occasion de s’exprimer en anglais.
Le point de départ est de nouveau une vidéo, réalisée par BBC radio 4 (radio publique généraliste, qui diffuse en particulier des émissions culturelles, scientifiques et historiques) intitulée “Go forth and multiply”, littéralement « avancez et multipliez », expression idiomatique inspirée d’une citation biblique (« Croissez et multipliez-vous ») qui signifie à peu près « allez voir ailleurs si j’y suis ». On peut la visionner à partir de ce lien ![]() , avec un petit défaut et une image hélas de qualité médiocre. Non seulement le contexte historique est décrit, mais une ouverture sur le lien entre la méthode décrite et le fonctionnement des ordinateurs modernes est en plus proposée.
, avec un petit défaut et une image hélas de qualité médiocre. Non seulement le contexte historique est décrit, mais une ouverture sur le lien entre la méthode décrite et le fonctionnement des ordinateurs modernes est en plus proposée.
En demandant aux élèves de repérer des thèmes ou des mots clés dans le film, il est toujours un peu difficile de les amener à sortir du champ mathématique : « puisqu’elle est prof de maths, c’est forcément ces mots-là qu’elle attend, rien d’autre ne va l’intéresser ». La DNL est une merveilleuse occasion pour désenclaver les mathématiques ! Ils citent donc “multiplication, arithmetic, base 2, addition…” et il faut insister pour obtenir “Ethiopia, London, coffee, trade, computer…”.
Je préfère donc demander à des groupes d’élèves de s’intéresser aux lieux, aux objets, aux personnes ou aux situations. S’ils voient d’abord un seul fil conducteur : la multiplication, ils sont heureux ensuite de voir que le thème du café revient comme un leitmotiv tout au long du film. Les élèves de ES apprécient le thème du commerce, tandis que les S sont en général plus sensibles à celui de l’informatique et tous sont épatés par le tour de magie multiplicatif.
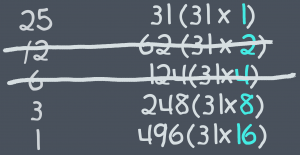
L’exemple ci-dessus montre comment ça marche, “how it works ?”. On prévoit deux colonnes : on place le plus petit nombre en haut de la colonne de gauche et le plus grand en haut de celle de droite. À gauche, on divise par deux en ne gardant que la partie entière du quotient à chaque fois, jusqu’à atteindre un résultat de 1. À droite, on double autant de fois qu’on a divisé à gauche. On barre toutes les lignes qui comportent un nombre pair à gauche et on additionne les nombres qui restent à droite. Comme par enchantement, on obtient le produit des deux nombres choisis.
Maintenant, voyons pourquoi ça marche, “why it works ?”.
On s’aperçoit que 25 = 1 + 8 + 16 = 1 + 23 + 24 si bien que 25 × 31 = 1 × 31 + 23 × 31 + 24 × 31, c’est-à-dire le total des nombres conservés dans la colonne de droite. Il est un peu plus difficile de faire percevoir aux élèves ce qui se passe dans la suite des divisions par 2 et pourquoi les lignes à quotient pair disparaissent.
$$\begin{aligned}
25 & = 2\times12+1\\
& = 2\times(2\times6)+1\\
& =2^2\times(2\times3)+1\\
& = 2^3\times(2+1)+1\\
& = 2^4+2^3+1\end{aligned}$$
À chaque fois qu’un quotient est pair (comme 12 ou 6), on peut le diviser encore par deux et utiliser l’exposant immédiatement supérieur. Au contraire, lorsqu’un quotient est impair (comme 25 ou 3), et qu’on ignore le reste égal à 1 de la division, la puissance de 2 correspondante apparaît dans l’expression du facteur de gauche (celui qu’on divise) sous forme de somme de puissances de 2, de sorte que cette ligne « compte ».
Cette méthode de multiplication est attestée dans l’Égypte ancienne, elle figure notamment dans le papyrus de Rhind qui date du XVIIIe siècle avant Jésus-Christ. Elle permet d’effectuer n’importe quelle multiplication en n’utilisant que les trois compétences : multiplier par deux, diviser par deux et additionner.
La vidéo attire notre attention sur le rôle des puissances de 2 et je suis donc amenée à initier les élèves à la numération en base 2. Pour cela, les élèves étant groupés (comme d’habitude) par tables de 4, je distribue à chaque table une bonne quantité de briques LEGO® (jusqu’à une centaine environ), toutes de la même taille. Je prends soin que certaines tables aient un nombre pair, d’autres un nombre impair de briques, et que certains nombres nécessitent de nombreuses puissances de 2 et d’autres très peu. La consigne est d’accrocher les briques par paires, en laissant éventuellement la brique-reste de la division par 2 de côté. Ensuite, on regroupe les paires par paires, avec éventuellement une paire restante, puis on fait des paires de groupes de 4, de 8, etc. Dans les groupes dont les membres sont soigneux et respectueux des consignes, c’est très efficace, la décomposition du nombre de briques sous forme de puissances de 2 saute littéralement aux yeux.


Dans les groupes qui se comportent de façon moins scolaire, l’activité peut donner lieu à un joyeux désordre : il y a des briques sous les tables, un assemblage de 16 briques se casse en 10 + 6, les élèves forment d’emblée des groupes de 32 briques s’ils sentent qu’ils ont assez de briques et surtout, des groupes se mettent à jouer (oui, les terminales sont contents de jouer particulièrement dans un cours d’option facultative qui a lieu de 16 à 18 heures). Même s’il me semble souvent utile d’accepter un peu de désordre pour laisser la créativité s’exprimer, on finit pas perdre de vue le but recherché : compter les briques selon les puissances de 2, bien voir qu’on a au maximum un lot de 2n briques, toucher du doigt le fait que deux lots de 2n briques, c’est un lot de 2n + 1 briques. J’en profite pour leur faire remarquer que, de même qu’il nous faut dix chiffres pour compter en base 10, il en suffit de deux pour compter en base 2. En dehors des élèves de série S qui suivent la spécialité maths, beaucoup semblent découvrir que l’écriture :
147 = 1 × 102 + 4 × 10 + 7
est basée sur les puissances de 10 ; par suite, il faut du temps pour comprendre l’analogie avec
147 = 1 × 27 + 1 × 24 + 1 × 2 + 1
et accepter l’idée de l’écriture 10010011 pour le même nombre en base 2.
Des prolongements pour se familiariser avec l’utilisation de la base 2 sont possibles : demander d’expliquer ce que signifie « avoir un 1 (ou un 0) comme dernier chiffre », ou bien « avoir 6 chiffres », jouer à poser des additions en base 2, compter jusqu’à 31 sur les doigts d’une seule main.
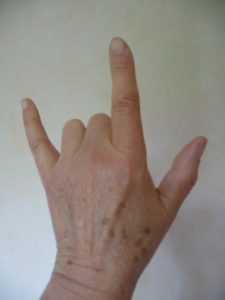
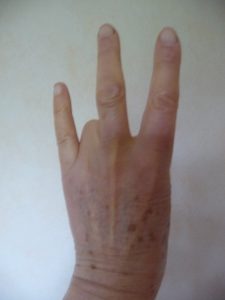
19 et 22.
Les mouvements du pouce, qui se lève et s’abaisse à chaque nombre lorsqu’on compte, permettent de deviner qu’il représente les unités, puis de comprendre le mécanisme.
La question « quels sont les avantages et les inconvénients de l’écriture des nombres en base 2, comparés à ceux de la base 10 ? » conduit à des échanges de réflexions intéressantes.
En voici quelques exemples : « la base 10 est plus facile à comprendre » (les élèves ne sont pas forcément convaincus que c’est parce qu’elle leur est familière) ; « l’écriture des nombres en base 10 est plus courte : 10011, c’est quand même plus encombrant que 19 » ; « la base 2 ne nécessite que l’usage de 2 symboles au lieu de 10 » ; « la base 2 est au cœur de l’informatique ».
Il est certain que, si tous les élèves de bonne volonté sauront appliquer cette méthode de multiplication en utilisant le vocabulaire approprié en anglais, seulement une partie sera capable de montrer sur un exemple la décomposition en base 2 de l’un des facteurs et très rares seront ceux qui auront compris le mécanisme général, sans parler de pouvoir l’expliquer en anglais.
La vidéo met l’accent sur le fait que cette méthode sous-entend l’utilisation de la base deux et donc contient en germe les idées qui conduisent au fonctionnement d’un ordinateur de nos jours. Les élèves sont souvent touchés par ce lien à des millénaires d’écart temporel. Il est intéressant de demander à chaque groupe d’élèves de produire un résumé des points marquants du film en leur donnant un fil conducteur différent pour chaque groupe : le café, le commerce, l’informatique, les lieux, les objets, les personnes. Cela favorise leur expression personnelle.
Ce travail, qui nécessite deux séances de deux heures environ, permet aussi aux élèves d’enrichir le thème « Magic tricks » qui pourra faire partie de la liste de sujets étudiés dans l’année, à fournir pour la deuxième partie de l’épreuve orale spécifique du baccalauréat.
Toutes ces activités illustrent un point qui est central dans mon enseignement de DNL : faire découvrir aux élèves des aspects culturels des mathématiques, sans mettre en jeu des concepts compliqués et en leur donnant l’occasion de s’exprimer.
Je recherche donc des sujets qui permettent une expression riche en anglais (plus que de faire des multiplications sans contexte, en tout cas) tant pour l’anglais généraliste que pour le vocabulaire spécifique. De plus, les élèves regardent sous un autre angle des notions aussi familières que l’écriture des entiers en base 10 et leur multiplication. Au delà de l’apport historique, qui contribue à réintégrer les mathématiques dans la culture générale, je suis convaincue que cet autre regard consolide chez les élèves la compréhension de la numération et des opérations.
Le travail de recherche et de choix de documents et de thèmes à traiter est très intéressant, mais assez lourd. Il a été partagé avec le groupe DNL de l’IREM de Caen ![]() , dont les membres mettent activement en commun les idées et les ressources que chacun a découvertes et d’autres collègues me signalent souvent des documents qui leur semblent adaptés pour les cours de DNL. Que toutes ces personnes en soient remerciées.
, dont les membres mettent activement en commun les idées et les ressources que chacun a découvertes et d’autres collègues me signalent souvent des documents qui leur semblent adaptés pour les cours de DNL. Que toutes ces personnes en soient remerciées.
Anne Reyssat, nouvellement retraitée, a enseigné les mathématiques en DNL (Discipline Non Linguistique) en section européenne anglais au lycée Salvador Allende d’Hérouville-Saint-Clair (Calvados).
