La multiplication en CE1
Dans cet article, Christine Choquet rend compte d’une activité menée dans une classe de CE1, autour d’une situation de modélisation de la multiplication inspirée du thé des maîtresses, activité tirée de l’ouvrage [5].
Christine Choquet
© APMEP Mars 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Introduction
À la rentrée 2016, les programmes de mathématiques du cycle 2 de l’école primaire insistent sur le développement chez tous les élèves de six compétences mathématiques ([7] p. 76). Par ailleurs, ils renforcent l’idée que les quatre opérations (addition, soustraction, multiplication, division) sont étudiées à partir de problèmes qui contribuent à leur donner du sens, en particulier des problèmes portant sur des grandeurs ou sur leurs mesures ([7] p. 75).
Pour cela, les professeurs des écoles sont encouragés à proposer aux élèves des problèmes issus de situations de la vie quotidienne et notamment des problèmes relevant des structures multiplicatives, de partages ou de groupements (multiplication/division).
Cet article propose un moyen de répondre à ces instructions officielles : la recherche et la résolution en classe de CE1 d’un problème inspiré de la situation le thé des maîtresses. Celui-ci nécessite, pour le résoudre, des recherches avec tâtonnements, il implique également de représenter la situation et/ou de la modéliser afin d’amener les élèves à réaliser qu’elle relève d’une situation multiplicative.
Le premier paragraphe est l’occasion de revenir, à travers quelques résultats de la recherche, sur l’enseignement de la multiplication au cycle 2 afin de justifier de l’intérêt de la situation choisie. Nous présentons ensuite une analyse des deux séances dédiées à ce problème, de leur mise en œuvre, des productions des élèves avant de conclure sur les réussites et les difficultés de cette classe face à de telles situations.
L’approche du sens de la multiplication dans la recherche
La construction du sens de la multiplication est amorcée en classe de CP (Cours Préparatoire) puis consolidée en CE1 (première année du Cours Élémentaire), l’approche privilégiée étant la recherche/résolution de problèmes relevant de l’addition réitérée ou de produit de mesures ([3] p. 69).
Cette dernière approche peut être abordée dans un premier temps en cherchant à déterminer le nombre de cases d’un damier [1] . Les élèves, lors d’une phase de recherche, constatent que ce nombre ne dépend que du nombre de lignes (L) et du nombre de colonnes (C), ce qui justifie que l’écriture L × C désigne le nombre de cases du damier. Il s’agirait de montrer ainsi aux élèves de CP/CE1, lors de manipulations et en utilisant le langage nouveau pour eux de la multiplication, que toute étude de grilles peut se traduire en symboles n × p et réciproquement l’utilisation des symboles renvoie aux grilles ([1] p. 16).
Les études liées à cette approche, réalisées depuis les années quatre-vingts par plusieurs auteurs[2][4] , amènent à la privilégier encore aujourd’hui dans les classes de cycle 2 mais nécessitent également de la questionner [5]. Elles montrent en particulier que la multiplication de deux entiers peut être définie de plusieurs façons mathématiquement équivalentes, mais principalement comme le nombre de cases d’objets rangés en un nombre de lignes et de colonnes déterminé par le multiplicande et le multiplicateur : les deux nombres comptent des ensembles de même nombre d’objets ( [4]p. 25). De plus, pour des élèves de CP/CE1 qui rencontrent pour les premières fois le signe × , cette définition règle le problème de la commutativité avant même l’écriture “a × b” puisqu’il s’agit du produit de deux grandeurs de même nature. En effet, le nombre de cases d’une grille est indépendant de son orientation comme de la façon de la percevoir et de la parcourir. Un quadrillage de a lignes sur b colonnes représente le même nombre de carreaux que a colonnes sur b lignes ou que b colonnes sur a lignes. Son usage conduit alors à avoir indifféremment une réitération de a éléments ou de b éléments indépendamment de toute convention sur un sens d’écriture ou un sens de lecture de l’expression mathématique […] ([6] p. 16).
Cependant, des limites à l’approche de la multiplication par le dénombrement d’objets disposés selon des configurations rectangulaires sont repérées et incitent des auteurs à questionner son usage ([5] et [3]). Il est estimé que cette approche est lourde et coûteuse en temps en CE1 et suscite des difficultés, notamment si le professeur des écoles y a recours non seulement pour donner du sens à la multiplication mais également pour justifier et enseigner la technique opératoire de la multiplication ([5] p. 244). Des difficultés ont en effet été relevées lors de l’évaluation des classes de CE2 de l’année 2000. Les élèves devaient calculer mentalement le produit 13 × 2 et la consigne était de dicter 13 × 2 (sans indication à l’enseignant sur les mots à prononcer). Ce calcul a été énoncé de trois manières différentes mais néanmoins valides : treize fois deux, deux fois treize et treize multiplié par deux et selon la traduction orale choisie, les réussites des élèves n’ont pas été identiques.
Par ailleurs, lors de la résolution d’un problème, l’écriture d’un produit est à expliciter aux élèves. En effet, pour résoudre le problème suivant : un enseignant distribue deux stylos à chaque élève. Il y a treize élèves. Combien a-t-il distribué de stylos en tout ?, les élèves peuvent rapidement le traduire par 2 + 2 + 2 + 2 + 2 + ⋯ autrement dit par treize fois deux. Mais l’introduction de l’écriture avec le signe × (ici 2 × 13) n’est pas aussi immédiate pour tous les élèves, elle demande un temps d’explication et peut constituer une difficulté même si elle est explicitement reliée par l’enseignant, à ce moment-là, aux activités centrées sur des configurations rectangulaires mettant en avant la propriété de commutativité (pour justifier que 2 × 13 et 13 × 2 sont deux écritures équivalentes et signifier alors que pour calculer 2 × 13, on a le choix et on peut poser 13 × 2). De ce fait, une introduction à la multiplication en deux temps semble préconisée :
-
proposer d’abord quelques activités permettant aux élèves d’appréhender le sens premier de la multiplication sur la base de différentes écritures additives répétées sans utiliser le signe × mais en utilisant seulement le mot fois ;
-
puis, dans un deuxième temps, introduire le signe × en travaillant avec des configurations rectangulaires et aborder simultanément la notion de commutativité [3].
D’après nos observations en classe et le travail que nous menons lors de formations initiale ou continue, ces deux temps de découverte de la multiplication (mobilisant soit des additions réitérées, soit des configurations rectangulaires) semblent être, pour les professeurs, délicats à relier explicitement afin de permettre à tous les élèves d’appréhender la notion de multiplication.
Dans les paragraphes suivants, au regard des éléments précédents, nous présentons les enjeux des deux séances prévues par l’enseignant puis analysons leur mise en œuvre ainsi que les productions des élèves de CE1.
Présentation de l’énoncé proposé en classe
L’énoncé proposé aux élèves est issu de la situation le thé des maîtresses ([5] p. 94) :
Chaque jour, les maîtresses d’une école utilisent 14 sucres pour le thé qu’elles boivent pendant la récréation. Combien de jours va durer la boîte de sucres?
Du matériel est prévu par les auteurs : pour la classe, sur le bureau de l’enseignant, un paquet d’un kilogramme de sucre en morceaux (ouvert afin de distinguer 14 rangées de 4 sucres et 3 étages) et pour chaque enfant, une copie de représentations de différents paquets. Dans l’ouvrage [5], ce problème est le 7ème d’un chapitre consacré aux problèmes pour apprendre à chercher. Il s’agit d’atteindre deux objectifs prioritaires: savoir décomposer un problème en sous-problèmes et savoir interpréter à chaque étape de la résolution ce qu’on a obtenu et ce qu’il reste à faire pour terminer le problème (Ibid., p. 94). Du point de vue des procédures, il est notamment attendu des élèves qu’ils considèrent le nombre de rangées (puisqu’une rangée représente un jour) ou qu’ils cherchent le nombre total de sucres par dénombrement des sucres (addition un à un, par 4, par 14 ou multiplication 4 × 14, 4 × 3) puis déterminent ensuite le nombre de jours (quotient).
La lecture des documents de préparation de l’enseignant observé révèle que celui-ci s’est approprié la situation et a fait des choix quelque peu différents afin d’atteindre des objectifs en lien avec les instructions officielles en vigueur. Celui-ci prévoit un paquet de sucres mais le dissimule tout d’abord à la classe, il envisage de ne le montrer qu’après un temps de recherche des élèves afin de valider certaines réponses et/ou d’aider les élèves en difficultés face au problème. Il décide en fait de seulement projeter une photographie du paquet ouvert et de distribuer une copie de cette photographie à chaque élève. Les élèves n’auront donc pas face à eux la vraie boîte.
Le professeur a fait ces choix en lien avec les objectifs fixés pour ses deux séances, qui diffèrent de ceux de l’ouvrage [5] : il vise le développement des compétences chercher, représenter et modéliser ainsi qu’un lien avec la modélisation d’une situation multiplicative, tout cela afin de donner du sens à la multiplication. Il attend de ses élèves qu’ils mettent au point une démarche de résolution après avoir identifié le problème et s’être représenté la situation : soit un dénombrement (un à un ou par paquets de 14), soit un calcul (additions successives de paquets de 14, multiplication du nombre de rangées par le nombre d’étages).
Il envisage de conclure ces deux séances en insistant sur la démarche la plus efficace d’après lui pour des élèves de cet âge : le recours à la multiplication du nombre de rangées par le nombre d’étages.
Mise en œuvre des deux séances
Les deux séances ont lieu en fin de premier trimestre de l’année scolaire. Les 23 élèves de la classe de CE1 observée sont amenés toutes les semaines à travailler en petits groupes à la recherche/résolution de problèmes mathématiques.
Séance 1:
Phase de découverte ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5 min
Premiers essais individuels ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅10 min
Première mise en commun ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅10 min
Séance 2:
Recherche en groupes de quatre ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅20 min
Deuxième mise en commun ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅30 min
Synthèse ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅8 min
L’organisation des deux séances montre qu’un temps significatif est laissé aux recherches des élèves : 10 minutes lors de la séance 1 et 20 minutes lors de la séance 2.
Une mise en commun lors de chaque séance permet à la classe de faire le point régulièrement : sur les premières idées des élèves lors de la séance 1 puis sur les différentes productions lors de la séance 2.
Enfin, huit minutes lors de la séance 2 sont consacrées à une synthèse mettant en avant les différentes démarches de résolution envisageables, la vraie boîte de sucres est alors utilisée pour les expliquer à tous et les valider en vérifiant concrètement, par une manipulation des sucres, le résultat trouvé. L’enseignant a ensuite expliqué à la classe que, pour résoudre certains problèmes en mathématiques, plusieurs procédures peuvent exister. Il a surtout insisté sur celle qui semble être la plus efficace et qui utilise la multiplication : une rangée contient 14 sucres et il y a 4 rangées sur trois étages (14 × 4 × 3 donne le nombre de sucres d’une boîte ou 4 × 3 donne le nombre de jours cherché).
Étude des productions des élèves
Lors de la séance 2 avant la deuxième mise en commun, l’enseignant réussit à hiérarchiser les productions des élèves. Cette hiérarchisation lui permet d’une part de ne pas tout montrer à la classe (ce qui serait une perte de temps) et d’autre part de faire un choix dans l’ordre de présentation des solutions proposées par les élèves. Elle lui permet également de mettre en avant le fait que des démarches différentes sont envisageables.
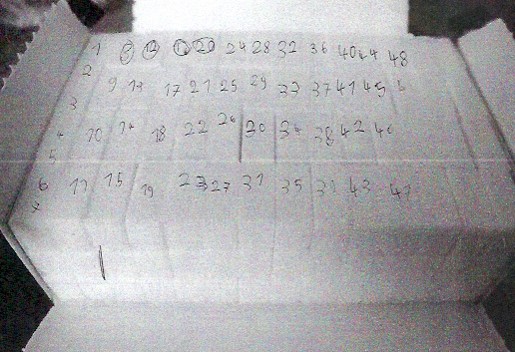
Production 1.
18 élèves sur 23 mettent en œuvre la procédure 1 : ils cherchent le nombre total de sucres en dénombrant un à un (et en marquant les sucres comptés). La plupart d’entre eux n’aboutit pas au résultat, notamment parce qu’ils ne comptent que les sucres visibles et ne pensent pas aux sucres cachés.
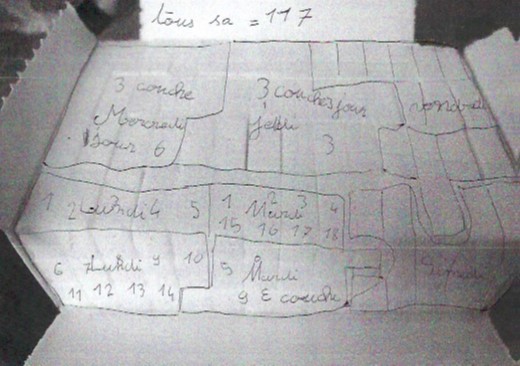
Production 2.
3 élèves sur 23 choisissent de faire des paquets de 14 sucres qu’ils représentent. Ces paquets ne sont pas tracés selon les rangées et les trois élèves ne pensent pas aux sucres cachés, ils ne tiennent compte que de ceux qu’ils voient.

Production 3.
2 élèves sur 23 adoptent cette stratégie. Ils se représentent tous les sucres, visibles et cachés selon trois étages.
Résultats des analyses
Plusieurs résultats découlent de l’analyse de ces deux séances, certains concernant la pratique de l’enseignant et d’autres les réussites et difficultés des élèves de cette classe.
L’analyse a priori du problème réalisée par l’enseignant avec l’aide des informations fournies dans l’ouvrage [5] lui permet de préciser les objectifs visés et de faire des choix cohérents quant à la mise en œuvre. En effet, souhaitant développer chez tous les élèves les compétences représenter et modéliser, la photographie distribuée aux élèves est un choix pertinent contrairement aux représentations proposées dans l’ouvrage [5]. Cette préparation lui permet également d’anticiper les différentes productions possibles des élèves et d’en prévoir une hiérarchisation afin d’organiser une deuxième mise en commun efficace, sans perte de temps et ciblée sur les objectifs fixés pour les deux séances.
L’observation des deux séances et l’analyse des productions des élèves permettent de constater que ceux-ci sont tous capables de comprendre l’enjeu du problème, de chercher et de s’engager dans une démarche personnelle de résolution. Ils éprouvent néanmoins des difficultés pour représenter et/ou modéliser la situation. En effet, la majorité des élèves (21 sur 23) n’a pas compris que des sucres étaient cachés, ils ont appliqué leur procédure seulement sur les sucres visibles sur la photographie. 
Conclusion
Nous avons présenté une activité menée en CE1 inspirée de la situation le thé des maîtresses[5]. La situation quelque peu transformée par l’enseignant lui permet de viser deux objectifs principaux : développer trois des six compétences mathématiques (chercher, représenter et modéliser) et présenter une modélisation de la multiplication afin de donner du sens notamment à l’écriture a × b.
Les résultats des analyses montrent qu’il est tout à fait possible de jumeler l’enseignement de la multiplication avec le développement de compétences mathématiques tout en ne perdant pas de vue les éventuelles difficultés pour des élèves de CE1 dans le cas de la représentation et de la modélisation de situations multiplicatives. Cette étude fournit en cela une piste permettant d’organiser pour les élèves une rencontre avec le monde fabuleux du calcul sachant que mathématiques et calcul sont indissociables ([2] p. 38). Elle permet également au-delà de cette situation d’insister sur l’intérêt pour un enseignant de réaliser une analyse a priori de l’énoncé afin de fixer précisément les objectifs d’apprentissage et d’anticiper au mieux la mise en œuvre des séances permettant de les atteindre.
Christine Choquet est maître de conférences à l’ÉSPÉ de l’Académie de Nantes. Elle intervient dans la formation des futurs professeurs des écoles.
Références
- APMEP. La multiplication des naturels à l’école élémentaire. ici Elem Math II. 1976.↩
- Michèle Artigue. « L’enseignement du calcul aujourd’hui : problèmes, défis et perspectives ». In : Repères IREM 54 ici (2004), p. 23-39.↩
- Valérie Bistos et Nicole Matulik. « Problèmes de multiplication et de division au cycle 2 ». ici In : Scéren, CNDP, (2012).↩
- Guy Brousseau. « Le calcul humain des multiplications et des divisions de nombres naturels ». ici In : Grand N 85 (2010), p. 13-41.↩
- Jacques Colomb et Roland Charnay. Apprentissages numériques et résolution de problèmes, CE1. Hatier, Collection ERMEL, 2005.↩
- APMEP Commission Premier degré. « 5 fois 3 est-il égal à 3 × 5 ? » ici In : Bulletin Vert 457 (2005).↩
- Bulletin officiel de l’éducation nationale. « Programme d’enseignement du cycle des apprentissages fondamentaux (cycle 2) ». ici In : 2015.↩

