Une bonne pratique consiste à encapsuler le calcul de la factorielle de \(n\) dans une fonction fac à un paramètre, qui prendra \(n\) comme argument et retournera en résultat sa factorielle. Une fonction se voit alors comme une boîte noire (un circuit virtuel) prenant zéro, une ou plusieurs entrées et retournant zéro, un ou plusieurs résultats². En voici une définition :

Dans cette optique, programmer consiste à construire de telles boîtes noires fonctionnelles et à les connecter pour résoudre un problème. Un peu à la manière d’un électronicien qui construit un circuit imprimé à partir de composants.

Le matheux habitué à définir la factorielle par récurrence : \[n !=\begin{cases}
1 &\text{si $n = 0$}\\
(n-1) !\times n &\text{si $n > 0$}
\end{cases}\] sera sans doute heurté par la nécessité de passer par une boucle for étrangère à la pensée mathématique pure. Peut-on coder telle quelle la définition ci-dessus en Python ?

La récurrence

Dans le programme de Première spécialité maths, les aspects calculatoires sont mis en avant, ce qui est une bonne chose pour tout le monde (du scientifique au simple praticien du calcul), et l’introduction du thème algorithmique et programmation, enseigné dans le cadre du cours de mathématiques, était attendu depuis des lustres. Mais les activités autour de la démonstration et plus généralement de la rigueur — remplacée par un large appel à l’intuition — m’ont paru manquer d’assurance, notamment dans le cours d’analyse.

Prenons l’exemple de la récurrence. Celle-ci est hors-programme en Première, aussi bien en maths qu’en programmation. Pourquoi avoir choisi d’enseigner les suites définies par récurrence sans aborder, simplement mais franchement, le principe de récurrence, dans sa double articulation : démontrer et construire, en profitant de la symbiose entre le cours de mathématiques et celui d’algorithmique ?

Les exemples fournis dans les livres de maths de Première (pour ne citer que ce niveau) utilisent essentiellement la boucle for. Cela est pertinent dans le cadre d’un cours de physique, où le déroulement temporel et pas à pas d’un algorithme se comprend. Mais dans un contexte de mathématiques, il me paraît intéressant d’insister sur les concepts de fonction (ce que demandent d’ailleurs les instructions officielles) et de récurrence (mise étrangement de côté). Je laisse aux matheux le soin de se battre (ou pas) pour faire émerger la récurrence comme technique de démonstration en Première dans le cadre du travail sur la preuve, qui me semble tardif. J’ai souvent eu l’occasion d’entendre les plaintes des professeurs de mathématiques en Licence sur la difficulté des étudiants à rédiger une démonstration simple en 2 voire 3 année. Ayant étudié dans les années 1970, on me taxera peut-être de nostalgique : j’assume.

Il existe des dizaines de langages autres que Python, mais tous se rattachent à une ou plusieurs manières majeures de programmer. Un langage de programmation est un véhicule de la pensée : il permet d’exprimer des idées et de les organiser à travers une méthodologie qui lui est propre. Les langages impératifs s’appuient sur les variables et les instructions qui vont les modifier, dont la conditionnelle et la boucle ; Python en fait partie. Les langages orientés objets permettent de construire un monde d’objets communiquant par envois de messages. Les langages fonctionnels mettent en avant le concept de fonction et remplacent la boucle par la récurrence³.

Ces trois paradigmes de programmation ne sont pas les seuls et Python utilise les deux premiers en s’autorisant quelques incursions dans le troisième, gage d’une certaine souplesse. Cela permet au programmeur de choisir celui qui lui paraît le plus adapté à une tâche. Ça calcule et c’est propre (à la preuve de correction près).

Arrêtons-nous un peu sur le modèle fonctionnel, celui des modifications temporaires de mémoire issues de la substitution \(x=a\), \(y=b\) des arguments \(a\) et \(b\) aux paramètres \(x\), \(y\) d’une fonction \(f\), produisant la valeur de sortie \(f(a,b)\). Que les dites fonctions puissent être composées n’étonnera personne, ni qu’une fonction fasse appel à elle-même ! La définition par récurrence de la fonction \(n \mapsto
n !\) serait :

Ce programme est plus adapté à la machine qu’à l’humain car il nécessite de descendre jusqu’au cas de base avant de commencer à calculer, donc de mettre en mémoire les multiplications en attente.

\[\begin{aligned}
\mathtt{facr}(3)& \\
& \leadsto \mathtt{facr}(2) \times 3\\
& \leadsto (\mathtt{facr}(1) \times 2) \times 3\\
& \leadsto ((\mathtt{facr}(0) \times 1) \times 2) \times 3\\
& \leadsto ((1 \times 1) \times 2) \times 3\\
& \leadsto (1 \times 2) \times 3\\
& \leadsto 2 \times 3\\
& \leadsto \fbox{6}\end{aligned}\] A contrario, avec une boucle for, les calculs se font pas à pas avec une quantité de mémoire réduite.

Le professeur de mathématiques ne dit pas autre chose lorsqu’il écrit \(u_0=-4,~ u_{n+1} = 2u_n+3\). Programmer le calcul du terme général \(u_n\) avec une boucle for permettra de l’obtenir :

Il me paraît tout à fait naturel de programmer par récurrence la définition de cette suite qui est définie par récurrence, c’est la moindre des choses. Et la justification informatique du calcul est au même niveau que la justification mathématique de la définition (une suite est une fonction). Mais attention, en programmation, on passe de \(n-1\) à \(n\) et jamais de \(n\) à \(n+1\), ce serait peut-être l’occasion pour nous matheux de nous mettre à jour ?

Cela fonctionne, et cela explosera si \(n\) dépasse une certaine limite (à cause des calculs en attente, dont le nombre est borné). Ce sera l’occasion d’expliquer la limitation des machines pour calculer et de justifier l’écriture d’une boucle plus efficace, ce qui n’est pas toujours faisable facilement. L’élégance de la définition originale est conservée et souvent suffisante. Et nous savons tous que le travail sur l’élégance n’est pas un luxe pour former un jeune aux mathématiques.

La récurrence en programmation a longtemps été considérée comme la cerise sur le gâteau. Elle est désormais tenue comme fondamentale, notamment dans la conception des algorithmes, quitte à les programmer avec une boucle ou toute autre optimisation par la suite si besoin.

La récurrence terminale

Les programmeurs, exploitant quotidiennement divers paradigmes de calcul, programment aussi certaines fonctions par récurrence. Mais ils savent quelque chose sur la récurrence qui a échappé pendant un siècle aux mathématiciens lorsqu’ils disent que la seconde version de la fonction u ci-dessus n’est pas une boucle. Non parce qu’elle n’utilise pas le mot for ou while, mais parce que lorsque la fonction u s’est invoquée elle-même pour obtenir le résultat de l’hypothèse de récurrence u(n-1), il reste autre chose à faire : il faut continuer le calcul en multipliant ce résultat par \({2}\) puis rajouter \({3}\). \[\begin{aligned}
\mathtt{u}(3)& \\
& \leadsto \mathtt{u}(2) \times 2+3\\
& \leadsto (\mathtt{u}(1) \times 2+3) \times 2+3\\
& \leadsto ((\mathtt{u}(0) \times 2+3) \times 2+3) \times 2+3\\
& \leadsto ((-4 \times 2+3) \times 2+3) \times 2+3\\
& \leadsto (-5 \times 2+3) \times 2+3\\
& \leadsto -7 \times 2+3\\
& \leadsto \fbox{$-11$}\end{aligned}\]

Comment ? Se pourrait-il qu’il ne reste rien à faire ? Mais oui, déjà dans un exemple bien connu : le PGCD «à la Euclide». Ce dernier nous a appris dans ses Éléments que le PGCD des entiers naturels \(a\) et \(b\) n’était autre que le PGCD de \(b\) et de \(a\,\,\text{modulo}\,\,b\). Le passage de \(b\) à \(a\,\,\text{modulo}\,\,b\) convergeant vers \(b=0\), l’algorithme s’écrit en Python, où modulo est l’opérateur % :

Après que la fonction pgcd s’est invoquée elle-même, il ne reste plus rien d’autre à faire, on dit que la récurrence est terminale. Formidable élégance de cet algorithme ! En réfléchissant un peu, on s’aperçoit que le rôle de la fonction pgcd consiste simplement à transformer le couple \((a, b)\) en le couple \((b, a\%b)\) jusqu’à ce que \(b\) devienne nul. \[\begin{aligned}
pgcd(12,30)& \\
& \leadsto pgcd(30,12) \\
& \leadsto pgcd(12,6) \\
& \leadsto pgcd(6,0) \\
& \leadsto \fbox{6}\end{aligned}\]

Aussitôt vu, aussitôt programmé avec une boucle, puisqu’au fond il semble se comporter comme une boucle ! Cette fois, le nombre de tours de boucle n’est pas connu⁴ et nous utiliserons la seconde boucle de Python nommée while (tant que).

Sinon, en se privant de la belle affectation entre couples offerte par Python et utilisée ci-dessus :

La dichotomie

Il m’arrive de voir, dans des ouvrages traitant d’algorithmes, des descriptions brutales avec une boucle for par exemple, qui sentent l’astuce à plein nez et demandent une réflexion avant de se convaincre de leur correction. Prenons le cas de la multiplication égyptienne. Je lis dans une page web d’un centre de formation :

Lorsqu’on utilise cette méthode égyptienne pour multiplier deux nombres \(a\) et \(b\) avec du papier et un crayon, on construit deux colonnes de nombres dont la première ligne est constituée des deux nombres \(a\) et \(b\). Les lignes suivantes sont obtenues dans la colonne de gauche en multipliant par deux le nombre précédent, et dans la colonne de droite en le divisant par deux (quotient entier //). On stoppe lorsque le nombre de droite vaut \(1\). Le produit \(a \times b\) est alors égal à la somme des nombres de la colonne de gauche dont le nombre correspondant à droite est impair.

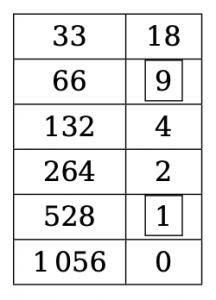
Méthode claire, testons-la avec \(a={33}\) et \(b={18}\).

Le tableau ci-dessous donne bien \(33\times 18=528+66=594,\)

avec uniquement des additions (\(a+a\) au lieu de \(2a\)) ainsi que des divisions par 2.

L’algorithme semble fonctionner : je peux le mettre en machine. Faire l’addition \(528+66\) à la fin m’imposerait de gérer la liste des lignes, je la ferai donc au fur et à mesure en gérant une variable résultat res en troisième colonne. Pour mon propos, je vous laisse le faire car en vérité j’ai autre chose en tête : la compréhension de cet algorithme. En l’observant attentivement, nous pouvons le saisir. Lorsque \(b\) est pair, la ligne suivante aura le même produit \(ab\). Lorsque \(b\) est impair, le produit diminuera de \(a\) car \(b\) // \(2\) — le quotient entier — est en réalité \((b-1)/2\) donc le nouveau produit sera \(2\times a\times (b-1) / 2 =
ab-a\), il faudra donc rajouter \(a\). Ce raisonnement vaut ce qu’il vaut. Est-il vraiment mathématique ? Sans doute, dans l’esprit des Anciens, qui décrivaient les calculs faits à la main pour convaincre le lecteur. Cela ne vaut pas un bon raisonnement algébrique, n’est-ce pas ?

Autre exemple de dichotomie : le calcul d’une puissance \(x^n\), où \(n\) est un entier naturel. Combien d’étudiants ai-je vu sécher sur un calcul par boucle et dichotomique de \(x^n\), donc en divisant à chaque tour de boucle l’exposant \(n\) par \({2}\) ? Pourtant un raisonnement par récurrence découpe immédiatement l’algorithme en trois cas. Prenons comme hypothèse de récurrence : pour tout \(y\), je sais calculer \(y^{n//2}\). \[\begin{aligned}
x^0 & =1\\
x^n & =(x\times x)^{n//2}\qquad\text{si $n$ est pair $> 0$}\\
x^n & =(x\times x)^{n//2}\times x\quad\text{si $n$ est impair}\end{aligned}\]

Difficile de faire plus concis. Mathématiquement clair, pas de problème pour prouver sa correction (par récurrence). La décroissance rapide de l’exposant \(n\), gros avantage de la dichotomie⁵, n’impose pas ici une version avec une boucle, mais cherchons-la pour le plaisir (ou parce que la récurrence est hélas hors-programme)… Je résiste à la tentation de refaire le coup de la multiplication égyptienne, en bricolant une boucle qui fera ce calcul. Je vous propose plutôt de bien regarder la structure de la fonction puis_dicho, notamment les lignes (2) et (3). La ligne (2) se comporte comme une boucle puisque il n’y a plus rien à faire après l’appel à puis_dicho. Ce n’est pas le cas de la ligne (3) : il restera à multiplier par x. Pouvons-nous forcer ces deux lignes à avoir la même forme ? Oui, elle calculent toutes les deux une puissance puis_dicho(…) multipliée par un nombre : 1 ou x. Introduisons donc la fonction auxiliaire et cherchons une définition intrinsèque de la fonction \(f\) n’utilisant ni l’opérateur puissance ** de Python ni la fonction puis_dicho.

• Si \(b=0\), utilisons (1) :

  \(f(a,0,c) = a^0 \times c = c\)

• sinon si \(b\) est pair, utilisons (2) :

  \(f(a,b,c) = a^b \times c = (a\times a)^{b//2} \times c\)

  \(\phantom{f(a,b,c)}= f(a\times a,b//2,c)\)

• sinon c’est que \(b\) est impair, utilisons (3) :

  \(f(a,b,c) = a^b \times c = ((a\times a)^{b//2} \times a) \times c\)

  \(\phantom{f(a,b,c)}= a^b \times c = (a\times a)^{b//2} \times (a \times c)\)

  \(\phantom{f(a,b,c)}= f(a\times a,b//2,a \times c)\)

D’où la définition par récurrence de \(f\) :

Nous voilà bien avancés, me direz-vous ? Ah, mais cette fois, il n’y a plus rien à faire après l’appel à f en lignes (2’) et (3’). La récurrence est terminale, elle peut être transformée à vue en une boucle, que nous rédigeons en fusionnant les deux fonctions précédentes.

Je vous laisse sur cette transformation de programme. L’euréka vient de la généralisation de la forme du résultat. Les matheux connaissent bien la puissance de la généralisation. Ici, pour calculer \(a^b\), nous nous sommes ramenés au calcul de \(a^b \times c\) : vous avez dit bizarre ?

Une telle généralisation n’est pas toujours aussi facile mais le fait de pouvoir calculer un programme ne vaut-il pas le détour ? Vous pourrez faire la même chose avec la multiplication égyptienne en vous inspirant de la récurrence :

\(a \times b = (a+a)\times \dfrac{b}{2}\)

et en suivant le même chemin pour obtenir une déduction mathématiquement saine de l’algorithme égyptien…

P.-S. Je me suis inspiré de la solution en ligne de l’exercice 11.19 de mon livre :
Python. Apprentissage actif. Pour l’étudiant et le futur enseignant (Ellipses, 2020) .

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Jean-Paul Roy a commencé sa carrière par six années d’enseignement en lycée durant lesquelles, dans le cadre d’un travail avec l’IREM de Paris, il a expérimenté un enseignement de la programmation en Terminale, avec les langages Lisp, Logo, Pascal et Prolog. Il a poursuivi dans cette voie en étant mis à disposition d’un centre de formation des enseignants du Secondaire à l’université Paris 6 jusqu’en 1991 où il a pris un poste de PRAG (PRofesseur AGrégé) au département informatique de l’université de Nice. Il est retraité depuis 2017.