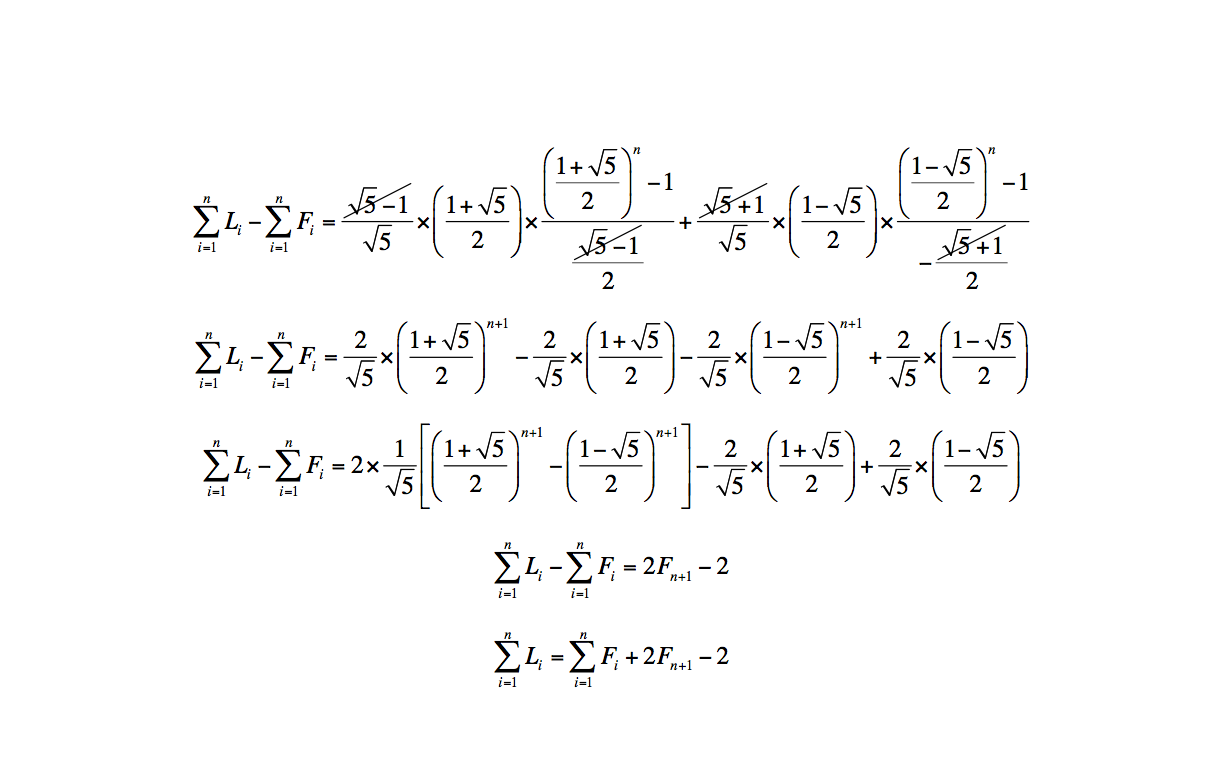Au fil des problèmes n° 535
Solutions

Frédéric de Ligt

© APMEP Septembre 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

535-1 Binero

Vous connaissez peut-être le Binero, ce jeu est de la même famille que le sudoku.

Il s’agit de remplir une grille incomplète, en général de dimensions \(6\times6\) à \(14\times14\), avec les quatre contraintes suivantes :

• la grille ne doit comporter que des 0 et des 1 ;

• chaque ligne et chaque colonne doit contenir autant de 0 que de 1 ;

• sur chaque ligne et chaque colonne, il n’y a pas plus de deux nombres identiques à la suite ;

• il n’y a pas deux lignes ou deux colonnes identiques.

Combien de lignes différentes de longueur \(2n\) existe-t-il ?

Avant	Après

535-2 Triangulation numérique

Le \(n\)-ième nombre triangulaire \(\Delta_n\) s’obtient en ajoutant \(n\) au précédent et donc est la somme des entiers de 1 à \(n\). On a \(\Delta_1 = 1\) ; \(\Delta_2 = 3\) ; \(\Delta_3 = 6\) ; \(\Delta_4 = 10\) ; \(\Delta_5 = 15\) ; …

Par exemple, il est possible d’écrire 7 comme une combinaison des cinq premiers nombres triangulaires avec des coefficients valant \(+1\) ou \(-1\) :

\[\begin{aligned}
7& = -1-3+6-10+15\\
& = (-1)\Delta_1+(-1)\Delta_2 + (+1)\Delta_3+(-1)\Delta_4 +(+1)\Delta_5.
\end{aligned}\]

Plus généralement, il faudrait montrer que pour tout entier relatif \(N\) il existe un entier naturel \(n\) tel que \(N\) peut s’écrire comme une combinaison à coefficients \(+1\) ou \(-1\) des \(n\) premiers nombres triangulaires.

535-3 Avec Fibonacci et Lucas (Vincent Thill-Migennes)

On définit les suites \((F_n)\) et \((L_n)\) de Fibonacci et de Lucas par les relations de récurrence : \[F_{n +2} = F_{n +1} + F_n\text{ avec }F_1 = F_2 = 1\quad ;\quad
L_{n +2} = L_{n +1} + L_n\text{ avec }L_1 = 1\text{ et }L_2 = 3.\] Montrer que \(\displaystyle\sum_{i=1}^{n} L_i = \sum_{i=1}^{n} F_i + 2 F_{n+1}-2\).

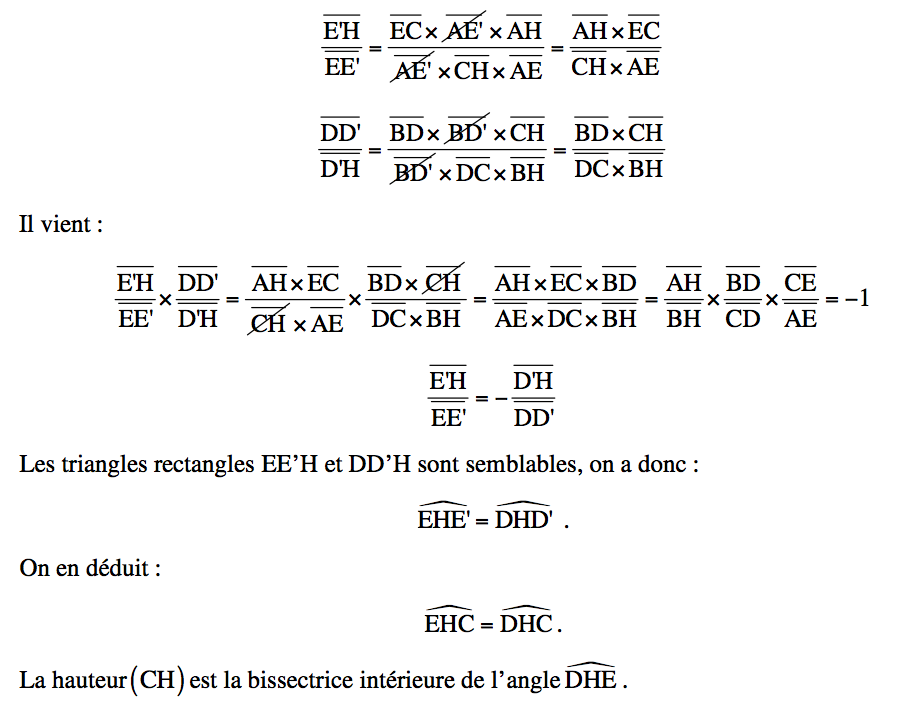
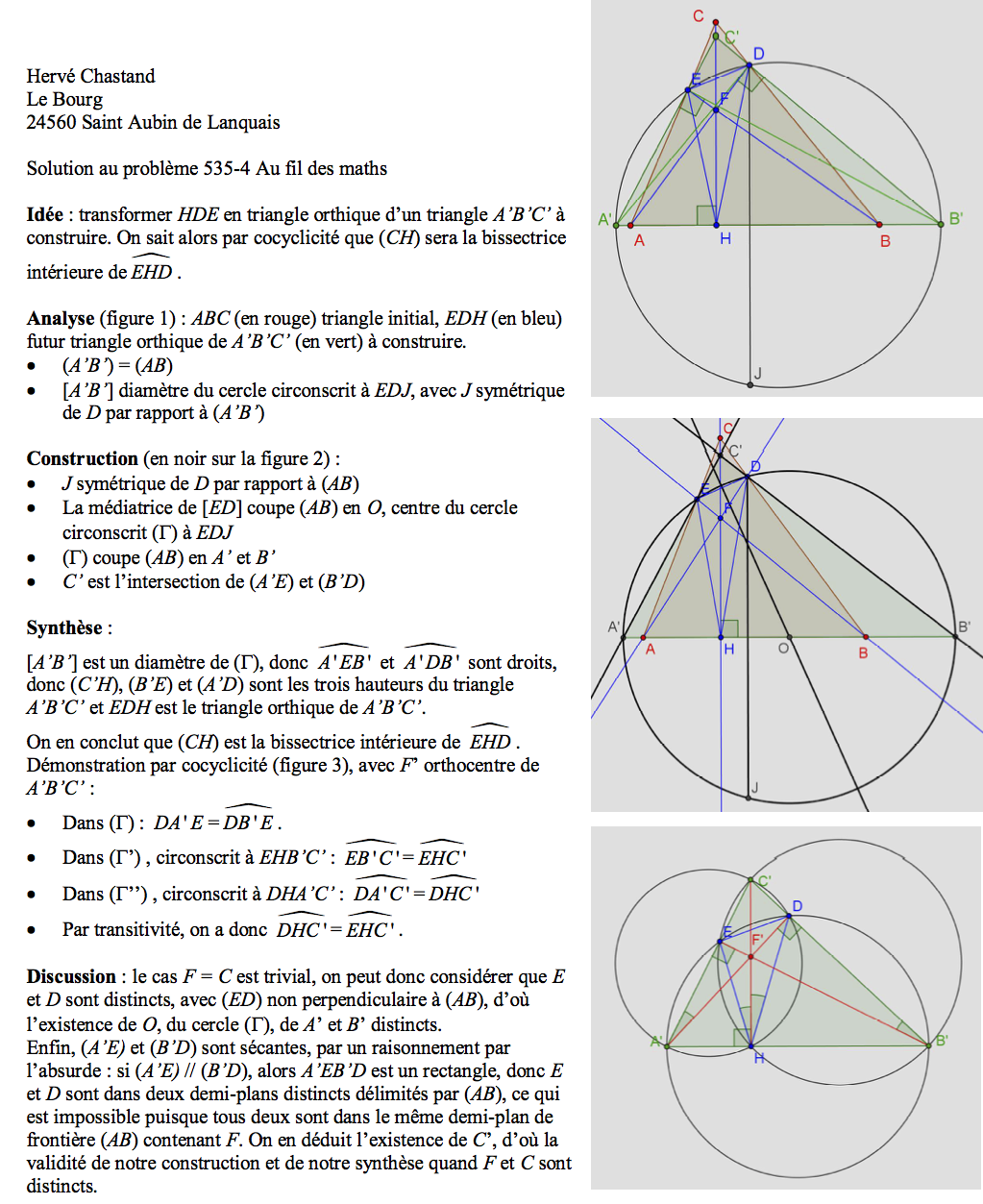
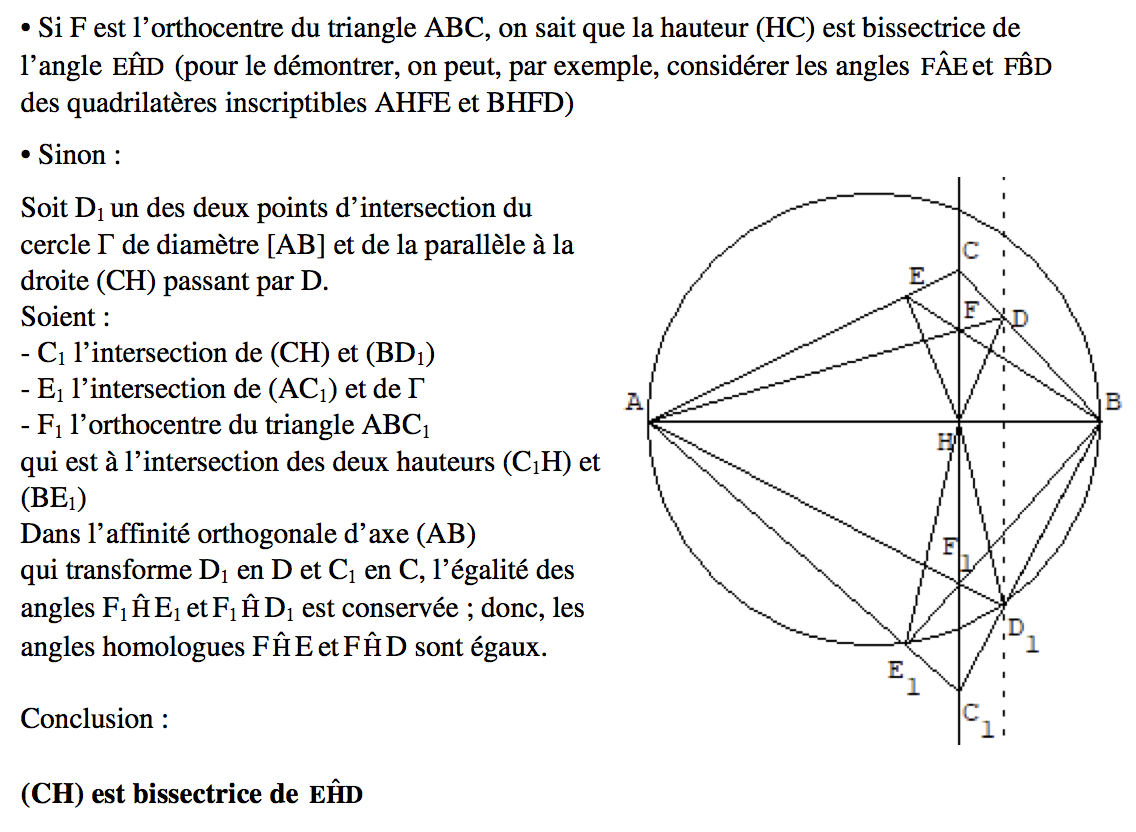
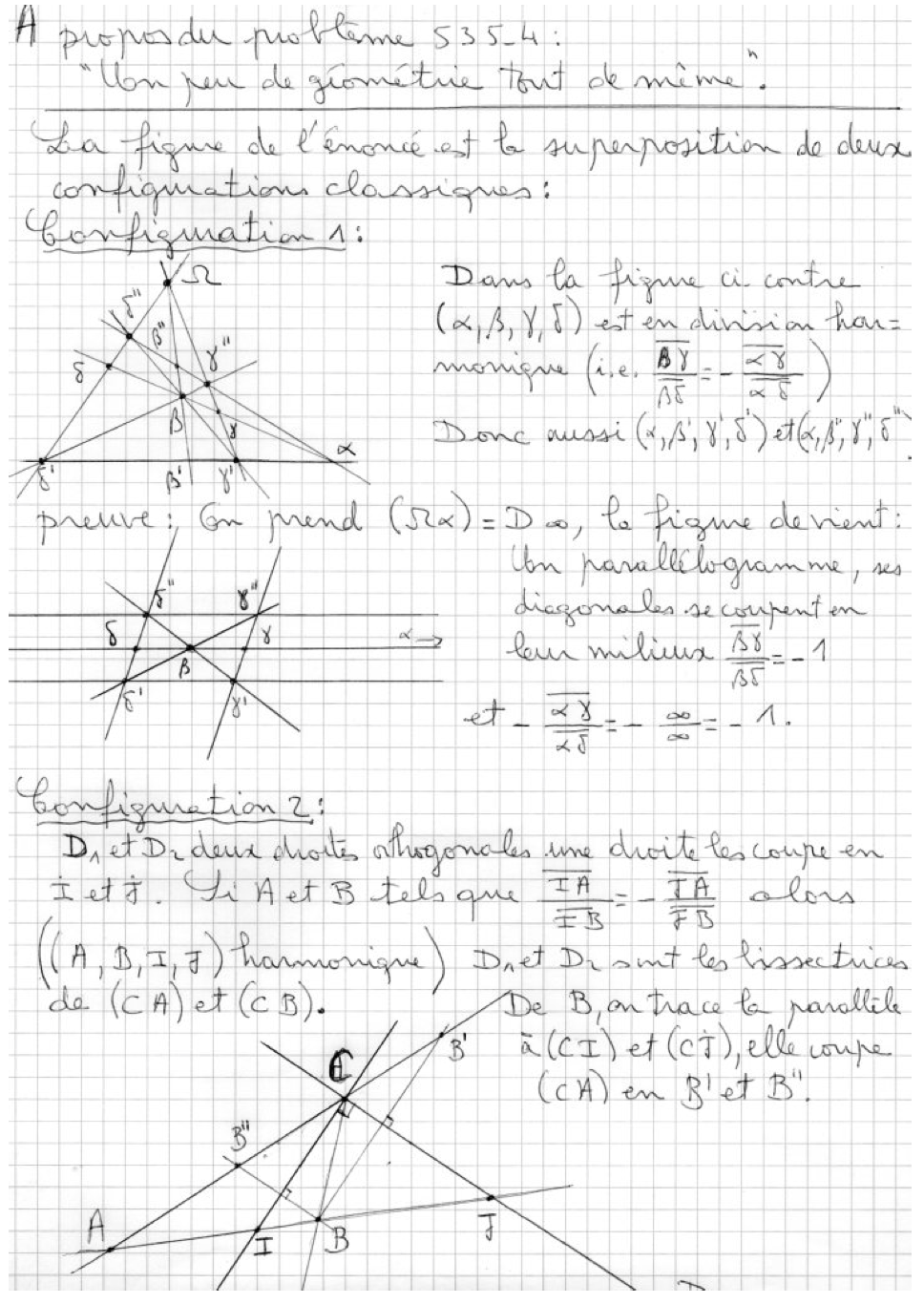
535-4 Un peu de géométrie tout de même

0.6 \(\mathsf{ABC}\) est un triangle, \(\mathsf{H}\) est le pied de la hauteur issue de \(\mathsf{C}\), \(\mathsf{E}\) est un point du côté \(\mathsf{[AC]}\) et \(\mathsf{D}\) un point du côté \(\mathsf{[BC]}\) tels que les segments \(\mathsf{[EB]}\) et \(\mathsf{[DA]}\) se coupent sur la hauteur \(\mathsf{(CH)}\) en un point \(\mathsf{F}\).

Montrer que la hauteur \(\mathsf{(CH)}\) se trouve alors être aussi la bissectrice intérieure de l’angle \(\widehat{\mathsf{EHD}}\).

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅