Élémentaire, mon cher Euclide !

Nous sommes tous des enfants d’Euclide. Depuis l’Antiquité, l’enseignement de la géométrie élémentaire s’est défini par rapport à lui, qu’on l’ait porté sur les autels ou qu’on l’ait honni. Pierre Legrand, dans cet article, voudrait donner une description sommaire de ce phénomène unique dans l’histoire des mathématiques.

Pierre Legrand

© APMEP Décembre 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Portrait d’Euclide par Juste de Gand peint vers 1474 ; le géomètre est par erreur identifié à Euclide de Mégare, selon une confusion courante à l’époque entre ce dernier et l’auteur des Éléments.

Alors, pour me sauver du doute, J’ouvre un Euclide avec amour. Il propose, il prouve ; et j’écoute, Et je suis inondé de jour. L’évidence, éclair de l’étude Jaillit et me laisse enchanté ! Je savoure la certitude, Mon seul vrai bonheur, ma santé ! Sully PRUDHOMME, Stances et poèmes (1865)

Ces vers d’un poète oublié de nos jours, mais qui fut très célèbre¹, montrent à quel point les Éléments d’Euclide ont pu être considérés comme l’archétype du raisonnement scientifique.

Si maintenant encore un sondage était organisé pour nommer le plus illustre mathématicien de tous les temps, il y a de fortes chances pour qu’une majorité avance le nom d’Euclide.

Je n’en veux pour preuve que cette citation de Pierre Desproges, tirée de son Manuel de savoir-vivre à l’usage des rustres et des malpolis (p. 97) :

« Je citerai celui qui, à mon humble avis, est le roi des cons. J’ai nommé le célèbre mathématicien Euclide qui affirme sans rire, je cite : La ligne droite est le plus court chemin d’un point à un autre. Quelle connerie ! Chacun sait en effet que la ligne droite NE PEUT ÊTRE le plus court chemin d’un point à un autre. SAUF, évidemment, si les deux points sont bien en face l’un de l’autre. »

Un « plus court chemin » qui a fait du chemin

Le problème, dans cette déclaration de Desproges, n’est pas son opinion sur Euclide, qui après tout était son affaire. C’est que la phrase qu’il incrimine ne figure nulle part dans les Éléments. La définition de la droite qu’on y trouve en première page est tout autre. En voici deux traductions :

• « La ligne droicte est celle qui est également comprise & estendue entre ses points. » (Denis Henrion, 1632).

• « La ligne droite est celle qui est tout également interposée entre ses points. » (François Peyrard, 1804, [3]).

Joignons-y pour le plaisir une traduction latine du  siècle : Recta linea est quae ex aequo inter sua signa sita est.

Quelle qu’en soit la formulation, la phrase n’a pas grand sens, mais elle en a largement autant que la définition donnée par Platon dans le § 137 du Parménide : « N’appelle-t-on pas […] droit ce dont le milieu est en avant des deux extrémités ? »²

En fait, Euclide était piégé : faute de disposer d’une axiomatique solide (qui n’arriva que deux mille ans plus tard), la construction impeccable qu’il rêvait de faire ne pouvait que reposer sur une base inconsistante.

Dans son ouvrage, l’idée de « plus court chemin » ne figure qu’indirectement via l’inégalité triangulaire, à laquelle il ne semble pas attacher d’importance spéciale. C’est la proposition 20 du livre I :

Deux côtés d’un triangle quelconque, de quelque manière qu’ils soient pris, sont plus grands que le côté restant.

La difficulté qu’Euclide n’avait pas perçue, Archimède l’a en revanche fort bien vue. Dans l’introduction de son traité De la sphère et du cylindre, il ne cherche pas à définir la droite et se contente d’énoncer un postulat (parmi plusieurs) :

J’admets les choses suivantes :

1. La droite est la plus courte des lignes ayant les mêmes extrémités.

Par la suite, on ne sait trop à quelle époque (mais sans doute dès l’Antiquité), cette propriété admise est devenue définition, y compris dans beaucoup d’éditions d’Euclide. On la trouve par exemple dans la première édition imprimée des Éléments, publiée en 1482 par Erhard Ratdolt : « Linea recta est ab uno puncto ad alium bravissimo extensio ».

La consécration définitive de ce point de vue est venue des Éléments de géométrie de Legendre (1794) [6], qui furent tout au long du  siècle le traité de référence. La formule magique, « La ligne droite est le plus court chemin d’un point à un autre », figure à la première page du texte. On la voit aussi dans les Élémens de géométrie de Lacroix (1799), principaux concurrents de ceux de Legendre. Elle a été reprise dans la grande majorité des manuels scolaires du XIX siècle et du début du XX^e. Citons cependant une bien jolie variante qui aurait ravi Pierre Desproges. Elle est tirée d’un Abrégé de géométrie pratique datant de 1840 : « Qu’est-ce qu’une ligne droite ? C’est celle dont tous les points qui la composent sont dans la même direction. »

Exception notable, en 1843, Eugène Catalan, dans ses Éléments de géométrie, n’hésitait pas à écrire : « Cette proposition : La ligne droite est le plus court chemin d’un point à un autre, ne définit rien ». À sa suite, les Leçons de géométrie élémentaire de Jacques Hadamard (1898) [4] font preuve d’une sage prudence :

La plus simple des lignes est la ligne droite, dont un fil tendu nous offre l’image. La notion de ligne droite est claire par elle-même ; pour la faire entrer dans nos raisonnements, nous considérerons la ligne droite comme définie par ses propriétés évidentes […].

Une autre histoire au long cours l’axiome d’Euclide

« Par un point pris hors d’une droite, on ne peut mener qu’une parallèle à cette droite. » Cet énoncé que l’on trouve par exemple tel quel dans le manuel d’Hadamard et que nous appelons l’axiome d’Euclide est presque aussi célèbre que le plus court chemin. Il a pourtant un problème : il est ambigu. Veut-il dire qu’on peut mener une parallèle et une seule, ou bien qu’on ne peut pas en mener plus d’une ?

En fait, depuis Euclide, tous les traités de géométrie (y compris celui d’Hadamard) distinguent bien ce qui est un théorème, l’existence d’au moins une parallèle, et ce qui est un axiome, l’unicité de cette parallèle.

Voici ce que cela donne chez Euclide³ :

Si une droite tombant sur deux droites fait les angles intérieurs plus petits que deux droits, les deux droites prolongées à l’infini se rencontreront du côté où les angles sont plus petits que deux droits.

Si une droite tombant sur deux autres droites [. . .] fait les angles intérieurs et placés du même côté égaux à deux droits, ces deux droites seront parallèles.

Signalons au passage que le mot « axiome », αξιωμα en grec, n’est pas utilisé par les mathématiciens antiques. Euclide emploie le mot αιτημα, demande ou requête (en un sens quelque peu juridique), dont l’équivalent latin est postulatum. On a longtemps parlé du « postulat d’Euclide », la forme « postulat » n’étant arrivée dans le français mathématique qu’au XVIII^e siècle. Et si le manuel d’Hadamard emploie le terme « axiome », il signale encore « postulat ».

La présentation faite par Euclide est restée très longtemps en usage : on la retrouve encore dans la Géométrie de Legendre ([6]) et dans celle de Lacroix, avec une différence : Legendre croit démontrer l’axiome, Lacroix a des scrupules, qu’il formule joliment : « C’est dans la difficulté de prouver immédiatement cette proposition, que réside l’imperfection de la théorie des parallèles. »

À la même époque, en 1795, les Elements of Geometry de John Playfair donnent pour la première fois une formulation proche de celle qui nous est familière :

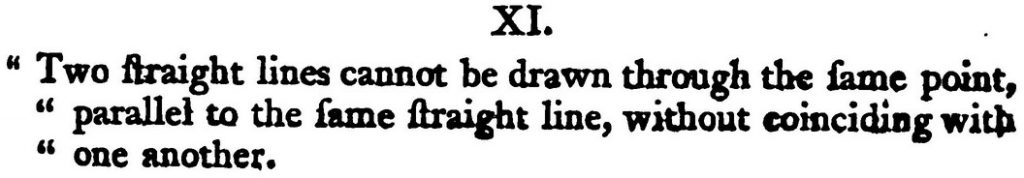On ne peut faire passer par le même point deux droites parallèles à la même droite sans qu’elles coïncident.

Notons qu’en toute modestie nationale les Britanniques, toujours fair-play, ne parlent pas d’axiome d’Euclide, mais de Playfair’s axiom.

Un culte bimillénaire

Pendant plus de deux mille ans, les Éléments furent la référence majeure des mathématiques de base, géométrie et arithmétique. Certains sont allés jusqu’à affirmer que ce livre est, après le Bible et le Coran, celui qui a connu la plus large diffusion. C’est manifestement faux, car les tirages des traités mathématiques n’ont jamais rien eu de commun avec ceux des Tintin ou des Astérix.

Si l’on compte en nombre d’éditions et non en nombre d’exemplaires, il est à peu près sûr, en revanche, qu’aucun autre ouvrage, hors la Bible, n’a connu un aussi interminable succès : des manuscrits en quantité, puis des centaines (on a parlé de plus d’un millier) d’éditions imprimées, parfois fidèles et souvent infidèles.

Comme le dit Charles Bossut dans son Histoire générale des mathématiques (1810) :

Jamais livre de science n’a eu un succès comparable à celui des Éléments d’Euclide. Ils ont été enseignés successivement, pendant plusieurs siècles, dans toutes les écoles de mathématiques, traduits et commentés dans toutes les langues : preuve certaine de leur excellence.

Il s’agit là d’un phénomène quasi religieux : la démarche d’Euclide était considérée comme un cheminement obligatoire. C’est ainsi que dans la Vie de monsieur Pascal, écrite par sa sœur Gilberte Périer, celle-ci raconte qu’à l’âge de douze ans il redécouvrit tout seul les fondements de la géométrie et « en vint jusqu’à la trente-deuxième proposition⁴ du premier livre d’Euclide ».

Ce respect mystique pour les Éléments a persisté jusqu’à nos jours. Nicolas Bourbaki lui-même y est allé de sa génuflexion :

ce qui était une démonstration pour Euclide en est toujours une à nos yeux ; et, aux époques où la notion a menacé de s’en perdre et où de ce fait la mathématique s’est trouvée en danger, c’est chez les Grecs qu’on en a recherché les modèles.

Éléments de mathématique,
livre I, Introduction

Les hérétiques

Cet aspect de livre saint que revêtent les Éléments a un inconvénient majeur : dans tout culte la tentation des exégèses aventureuses, voire des hérésies, n’est jamais loin. Et plus longtemps dure le culte, plus le phénomène s’amplifie. La définition de la droite et l’axiome des parallèles sont loin d’être les seuls cas où traducteurs et commentateurs ont pris des libertés avec la pensée du maître.

L’Histoire des mathématiques de Jean-Étienne Montucla (1758) n’est pas tendre pour ces déviations :

En vain divers Géomètres, à qui l’arrangement d’Euclide a déplu, ont tâché de le réformer, sans porter atteinte à la force des démonstrations. Leurs efforts impuissans ont fait voir combien il est difficile de substituer à la chaîne formée par l’ancien Géomètre, une autre aussi ferme & aussi solide.

Un demi-siècle plus tard, Lagrange et Delambre5 furent encore plus sévères dans le rapport (voir ci-contre) qu’ils présentèrent le 19 mars 1804 à l’Académie des Sciences. Mais les « étranges libertés » dont parle leur rapport ne vont en fait pas très loin. Il s’agit presque toujours de modifications de détail laissant intactes la structure et la démarche de l’œuvre.

Les premiers iconoclastes

De temps à autre des voix discordantes se sont cependant fait entendre. La première contestation marquante est venue des messieurs de Port-Royal, grands amis de Pascal. La logique, ou l’art de penser (1662) [1], d’Antoine Arnauld et Pierre Nicole⁶, contient dans sa quatrième partie un chapitre VIII, « De quelques défauts qui se rencontrent d’ordinaire dans la méthode des géomètres », qui est une attaque en règle contre la démarche d’Euclide. Les défauts en question sont au nombre de cinq :

Défaut 1 : « Avoir plus de soin de la certitude que de l’évidence et de convaincre l’esprit que de l’éclairer. »↩ Défaut 2 : « Prouver des choses qui n’ont pas besoin de preuve ».↩ Défaut 3 : « Démonstration par l’impossibilité ».↩ Défaut 4 : « Démonstrations tirées par des voies trop éloignées ».↩ Défaut 5 : « N’avoir aucun soin du vray ordre de la nature ».↩

Les défauts 2 et 3 semblent une mauvaise querelle : le besoin de preuve est chose assez subjective, et la démonstration par l’absurde chose fort naturelle. En revanche, les autres critiques sont pleinement justifiées.

Le défaut 1 apparaît dès les premières pages des Éléments : ceux-ci débutent en fanfare par l’accumulation de trente-cinq définitions. En outre, Euclide ne dit jamais où il va ni pourquoi il procède comme il le fait.

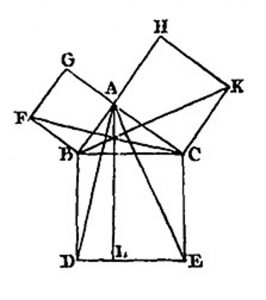
Pour se convaincre du défaut 4, il suffit de penser à la démonstration du théorème de Pythagore (livre I, proposition 47), le fameux pont aux ânes7 dont la célébrissime figure (figure 45 de l’édition Peyrard, ci-contre) fut le cauchemar de générations de collégiens.
Quant au défaut 5, je laisse parler Arnauld et Nicole :

Arnauld voulut prêcher d’exemple. Il publia anonymement, en 1667, ses Nouveaux Élémens de Géométrie. Ils connurent un certain succès, furent réédités en 1683 mais sombrèrent ensuite assez vite dans l’oubli.

Le premier concurrent sérieux

Alexis Clairaut, dont on a dit qu’il avait appris à lire dans les Éléments d’Euclide, publia en 1741, à l’âge de vingt-huit ans, des Élémens de géométrie [2] qui sont en quelque sorte un anti-Euclide. Il suffit pour le voir de comparer, par exemple, sa démonstration du théorème de Pythagore à celle d’Euclide⁸.

La page de titre (ci-contre) de la première partie du livre donne bien son esprit : faire naturel et concret quitte à sacrifier la rigueur. C’est ainsi, par exemple, que quatre pages sont consacrées à l’usage du rapporteur. Un exemple tout à fait typique de sa façon de faire est son introduction des parallèles : Dans la construction des ouvrages, comme des remparts, des canaux, des rues, etc. on a besoin de mener des lignes parallèles, c’est-à-dire des lignes dont la position soit telle que leurs intervalles aient partout pour mesure des perpendiculaires de même longueur. Il ne s’agit donc en aucune façon de bâtir un édifice irréprochable, mais de rendre le lecteur capable d’utiliser de façon autonome un certain nombre de notions simples.

Le livre fit du bruit : au moins cinq éditions en anglais et en allemand, trois en italien et en espagnol, deux en polonais et en suédois. En France, il fut utilisé par certains manuels scolaires, sous une forme plus ou moins adaptée, jusque vers les années 1860.

Mais cette pédagogie nouvelle était trop révolutionnaire pour supplanter l’ancienne et Euclide resta le modèle dominant.

L’héritier légitime

Ce que je viens de dire est inexact. Si le modèle dominant tout au long du  siècle et au début du resta euclidien, la référence suprême ne fut plus les Éléments d’Euclide, mais les Éléments de géométrie de Legendre   [6] apparus en 1794.

L’ambition de Legendre, à la différence de celle de Clairaut, n’était aucunement pédagogique. Il s’agissait, en reprenant la démarche d’Euclide, de la corriger pour la rendre irréprochablement rigoureuse.

L’organisation de l’ouvrage est calquée sur celle de son vénérable prédécesseur : division en livres (il y en a huit), chaque livre comportant un lot de définitions suivi d’une kyrielle de propositions. Comme Euclide, Legendre n’explique aucunement sa démarche. Il s’est évidemment heurté aux mêmes problèmes que son maître et notamment à l’axiome des parallèles. Legendre croyait fermement qu’on pouvait le démontrer et, au fil des éditions, il en a donné plusieurs preuves aussi ingénieuses que fausses. La correction formelle du livre et sa fidélité au cheminement euclidien eurent leur récompense : douze éditions du vivant de l’auteur et de nombreuses traductions. En outre l’ouvrage inspira plusieurs générations de manuels, phénomène qui dura, avec quelques accommodements, jusqu’au début du siècle.

Un début d’émancipation

Dans les programmes scolaires, la première rupture avec la tradition euclidienne vint par la réforme de 1902-1905, celle qui donna aux études scientifiques une dignité égale à celle des études littéraires.

Pour la géométrie dans les grandes classes, deux changements majeurs : introduction des transformations (translation, rotation, symétrie…) et, en terminale, introduction des vecteurs. Mais surtout, au niveau de ce qui est maintenant le collège, le point de vue officiel formulé dans les instructions du 27 juillet 1905 était plus proche de Clairaut que d’Euclide :

L’enseignement de la géométrie doit être essentiellement concret ; il a pour but de classer et de préciser les notions acquises par l’expérience journalière, d’en déduire d’autres plus cachées et de montrer leurs applications aux problèmes qui se posent dans la pratique.

Cette révolution ne se fit pas sans mal, et dès 1920 se produisit un retour en arrière. Les choses continuèrent ensuite cahin-caha jusqu’aux années 1960.

À bas Euclide

L’apostrophe « À bas Euclide ! » fut lancée par Jean Dieudonné (ci-contre) en novembre 1959, lors du colloque international de Royaumont qui fut à l’origine de la réforme des « mathématiques modernes » (entamée en 1968, progressivement abandonnée à partir de 1975). L’idée de Dieudonné n’était pas d’attaquer la démarche ou les méthodes du grand ancêtre, mais de contester la part excessive donnée par les programmes de l’époque à la géométrie et notamment à « des joujoux artificiels comme les triangles ».

Paradoxalement, la réforme des « mathématiques modernes » qu’il appelait de ses vœux fut un retour aux ambitions et aux méthodes d’Euclide : construire la géométrie sur des bases irréprochables, quitte à sacrifier l’intelligibilité immédiate et même l’intelligibilité tout court (définition de la droite comme un ensemble muni d’un lot de bijections ad hoc, définition d’un vecteur comme classe d’équivalence de bipoints, définition d’un angle comme classe d’équivalence de couples de demi-droites¹⁰, etc.).

N’oublions pas en outre que Dieudonné était l’un des membres les plus actifs du groupe Bourbaki, dont l’œuvre majeure porte le titre d’Éléments de mathématique et adopte le même type de plan qu’Euclide : pour chaque livre du traité une liste de définitions suivie d’un chapelet de théorèmes¹¹.

Le véritable « À bas Euclide ! » figure dans un ouvrage posthume du philosophe et historien des sciences Imre Lakatos (1922-1974), Preuves et réfutations ([5] pp. 181 et 183) :

Euclide a été le mauvais génie particulièrement de l’histoire et de l’enseignement des mathématiques, tant au niveau propédeutique qu’à celui de la création.

Lakatos appuie cette mise au pilori sur une argumentation qui n’est pas plus tendre :

La méthodologie euclidienne a développé un certain style de présentation obligatoire auquel je ferai référence par l’expression « style déductiviste ». Dans ce style on commence par une liste précautionneuse d’axiomes, de lemmes ou de définitions. Les axiomes et les définitions paraissent fréquemment artificiels et d’une complication déroutante. On ne dit jamais comment ces complications sont nées. La liste d’axiomes et de définitions est suivie de théorèmes soigneusement mis en mots, encombrés de conditions pesantes ; il semble impossible que quiconque ait jamais pu les inventer. Le théorème est suivi de la preuve.

L’étudiant en mathématiques est obligé, dans le rituel euclidien, de suivre ce tour de prestidigitation sans poser de questions sur le contexte ni sur la façon dont est réalisé l’escamotage.

Le cercle se referme : cet éreintement pourrait tout aussi bien s’appliquer aux Éléments de Bourbaki qu’à ceux d’Euclide.

Post-scriptum

Quelques esprits chagrins pourront s’étonner que j’aie réussi à parler longuement de l’œuvre d’Euclide sans dire un mot de l’homme lui-même. Le fait est qu’on ne sait rien sur lui. Ce que l’on trouve de plus précis se réduit à quelques lignes de Proclus¹² (qui vécut sept ou huit siècles après le grand géomètre, donc peut difficilement être considéré comme un témoin direct).

Euclide […] a mis en ordre divers travaux d’Eudoxe, amélioré ceux de Théétète, et aussi donné des démonstrations irréfutables pour ce que ses prédécesseurs n’avaient pas assez rigoureusement prouvé.

Proclus affirme ensuite qu’Euclide vivait au temps de Ptolémée I, donc au  siècle avant notre ère, et ajoute ceci :

On dit que Ptolémée demanda un jour à Euclide s’il n’existait pas en géométrie une voie plus courte que celle des Éléments, et il répondit qu’il n’y avait pas de voie royale en géométrie.

Beau sujet de méditation…

Bibliographie

1. Antoine Arnauld et Pierre Nicole. La Logique, ou l’Art de penser.  1664. ↩

2. Alexis Claude Clairaut. Élémens de géométrie.  1741. ↩

3. Euclide. Les élémens de géométrie d’Euclide. Trad. par François Peyrard. 1804. ↩

4. Jacques Hadamard. Leçons de géométrie élémentaire.  Armand Colin, 1898. ↩

5. Imre Lakatos. Preuves et réfutations. Hermann, 1984. ↩

6. Adrien-Marie Legendre. Éléments de géométrie.  1794. ↩

7. Jean Mawhin. Euclide revu par Legendre, ou des Éléments aux Éléments de Géométrie.  Cet article fournit quantité de détails intéressants. 2012.

8. Paul Tannery. La géométrie grecque. 1887. ↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Pierre Legrand a depuis longtemps un rôle actif au sein de l’APMEP, il a écrit de nombreux articles dans le Bulletin Vert.

---