Le cercle — peut-on en faire toute une histoire ?

Inspiré par notre fil rouge, Henry Plane a fouillé sa bibliothèque pour retrouver quelques archives évoquant le cercle. De petits trésors à (re)découvrir.

Henry Plane

© APMEP Décembre 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Cercle, disque, circonférence, rond, voire roue, cirque…Il faut constater que, dans un dictionnaire, chacun de ces mots fait appel aux autres. Et que fait le géomètre depuis qu’il a pris de l’importance lorsqu’on a su que la Terre était ronde ?…

Nous nous contenterons, dans cet article, de quelques échos sur le sujet, depuis quatre siècles, c’est-à-dire depuis la première traduction en français des livres dits d’Euclide : le Mardelé en 1620.

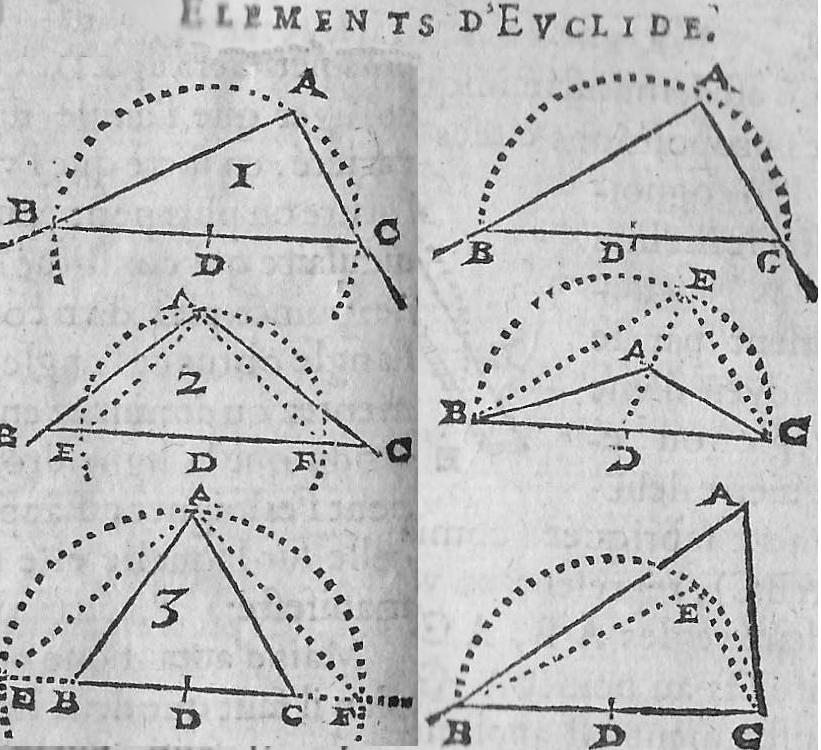
C’est le « Livre Troisième » qui est consacré au cercle, en voici le début :

On remarque, dès les premières pages de l’ouvrage, des figures où apparaissent des cercles.

En effet, sous une forme ou une autre, on dispose de l’outil compas :

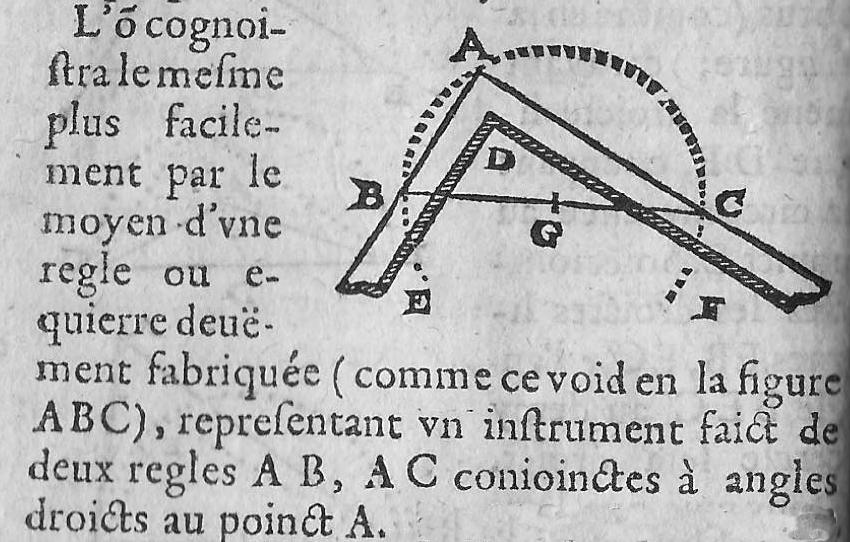
On constatera ensuite que les ouvrages du siècle vont s’écarter de l’ordre euclidien. Descartes ne s’attarde pas sur \(xx+yy\), Pascal étudie les « lignes du quart de cercle ».

Les « Éléments de géométrie » de Pardies (1671), qui eurent un grand succès à la cour de Pékin, montrent un ordre totalement différent.

Ainsi dès le début :

On parlera de tangente plus tard …

Viète, quant à lui, montre que les ressources des astronomes relatives aux triangles sphériques étaient supérieures à celles utilisées pour les triangles rectilignes. Si le « nombre utile aux sages » est connu avec une précision suffisante, les opérations qui l’entourent sont longues et lourdes à effectuer. Qui reconnaîtrait dans une équation du 45ème degré le sinus d’un arc de \(8\) degrés, comme le fit notre Vendéen ?

Pourtant, arpenteurs et artilleurs de l’époque auraient bien eu besoin de calculer avec des angles de diverses valeurs. Ils seront mis à l’aise par une découverte dans un autre domaine : ce sont Neper, avec les logarithmes, Briggs et Vlacq, avec les tables de sinus et de tangentes, qui vont simplifier les calculs. Les utilisations vont être fulgurantes dans toutes les branches des mathématiques. Euler et J. Bernoulli en témoignent dès le début du siècle.

Au passage nous noterons que, si les mesures des arcs de cercle, puis des angles, sont exprimées selon un système hérité de Babylone (\(90\) degrés de \(60\) minutes), celles des sinus vont imposer le système décimal plus d’un siècle avant le décret de la Convention en 1790.

Certes le cercle fait partie des coniques, florissantes au siècle, mais les ouvrages de géométrie sont, à présent, souvent publiés conjointement à ceux d’algèbre voire de trigonométrie : Clairaut, Bézout, Bossut… Il ne s’agit pas de « convaincre des sophistes obstinés » mais de s’adresser à un public voulant acquérir un certain capital de connaissances. L’époque, témoin des Lumières, pense à former des jeunes pour un monde nouveau. Plus on avancera dans ce siècle, plus on pensera à établir des programmes d’enseignement. Ce sera, en particulier, l’œuvre des organismes nationaux créés à la Révolution, avec Lacroix, Monge ou Legendre.

La géométrie y apportera sa rigueur et ses techniques. Ne vient-on pas de découvrir que tout ce qui se faisait avec la règle pouvait se faire avec le compas seul, c’est-à-dire avec des cercles !

Bonaparte a rapporté de sa campagne d’Italie le moyen de retrouver, grâce à Mascheroni, le centre perdu d’un cercle, au seul compas !

On veut déterminer le centre \(O\) du cercle \(\gamma\) (rouge).

Soit \(A\) un point arbitraire de \(\gamma\) et un cercle \(\gamma_1\) (cyan) de centre \(A\) sécant avec \(\gamma\) en \(B\) et \(C\).

Soit \(D\) l’autre point d’intersection des cercles \(\gamma_2\) et \(\gamma_3\) (pointillés) de centres respectifs \(B\) et \(C\) et passant par \(A\). Soit \(\gamma_4\)  (magenta) le cercle de centre \(D\) passant par \(A\).

Soit \(E\) et \(F\) les points d’intersection de \(\gamma_4\) et \(\gamma_1\). Le centre \(O\) cherché est le deuxième point d’intersection des cercles \(\gamma_5\) et \(\gamma_6\) (noirs) de centres respectifs \(E\) et \(F\) et passant par \(A\).

Peut-on dire que le XIX^e siècle a été celui du cercle ?

Glanons : le triangle, ou trois droites coplanaires, est muni d’un cercle circonscrit, d’un cercle inscrit, de trois cercles exinscrits, d’un cercle d’au moins neuf points… On en ajoutera.

Deux sécantes issues d’un même point : le géomètre y voyait des segments aux rapports inversement proportionnels, on y retiendra désormais un produit constant : la puissance d’un point par rapport au cercle, génératrice de l’inversion.

Avec deux cercles viendront les familles à points communs, à points de base…

Si un angle de grandeur constante, dont chaque côté passe par un point fixe, fait souvent souvenir d’Apollonius, d’autres figures avec cercles feront appel à de grands Anciens pour être distinguées.

\(\mathbb{C}\) entrera dans le jeu avec le plan complexe : \(z=a+\text{i} b\) mais aussi \(\rho \text{e}^{\text{i}\theta}\).

Survolons toujours : Edmond Rostand chantera au soleil « les ronds si beaux par terre ».

Puisque nous arrivons au XX^e siècle, seulement quelques extraits curieux de livres.

Méray, professeur à la faculté des sciences de Dijon, avait une conception de l’enseignement de la géométrie qui lui valut, entre autres, des démêlés avec la Direction de l’Instruction Publique. Le cercle n’arrivait qu’au chapitre 16, après l’espace (édition de 1903).

Les nombres en gras sont des renvois aux autres paragraphes du cours pour définir les termes utilisés.

La librairie Delagrave éditait une « géométrie » (programmes de 1909) destinée aux écoles primaires supérieures de jeunes filles avec des exemples à portée de la main.

Larousse n’édite pas que des dictionnaires. On pouvait trouver dans cette librairie un « Précis à l’usage de la classe de 5^e A et B » (programmes de 1930).

Cette page, et sa note de bas de page, n’ont que 80 ans !

Au XXI^e siècle… C’est à nous d’entrer en piste, circulaire comme au cirque ?

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Henry Plane, professeur de mathématiques retraité, est un membre actif de l’APMEP. Il appartient au groupe M:ATH (Mathématiques : Approche par des Textes Historiques) de l’IREM de Paris VII.