Le Grand Rampant
À l’occasion de la fête de la science 2018, le public parisien a pu découvrir le Grand Rampant, spectaculaire objet mobile, et son créateur Ulysse Lacoste, sous la verrière du Palais de la découverte. Pour ceux qui n’y étaient pas, cet article nous les présente et nous montre comment mathématique, art et mouvement peuvent se combiner pour créer un instant féérique.
Claudie Asselain-Missenard
© APMEP Mars 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Ulysse Lacoste est grand. Ulysse Lacoste est sympathique. Ulysse Lacoste est sculpteur. Il aime les objets. Il aime les sciences. Il aime le mouvement. Il réalise de ses mains des sculptures à la fois simples et belles, basées sur des formes géométriques élémentaires destinées à être en mouvement.
Il en fait des modèles à différentes échelles, certains suffisamment grands pour qu’un humain puisse s’y loger. Il nous montre la science et l’art en interaction, dans ces objets en mouvement où la matière et le corps humain s’allient dans un équilibre/déséquilibre maîtrisé, totalement surprenant et parfaitement esthétique.
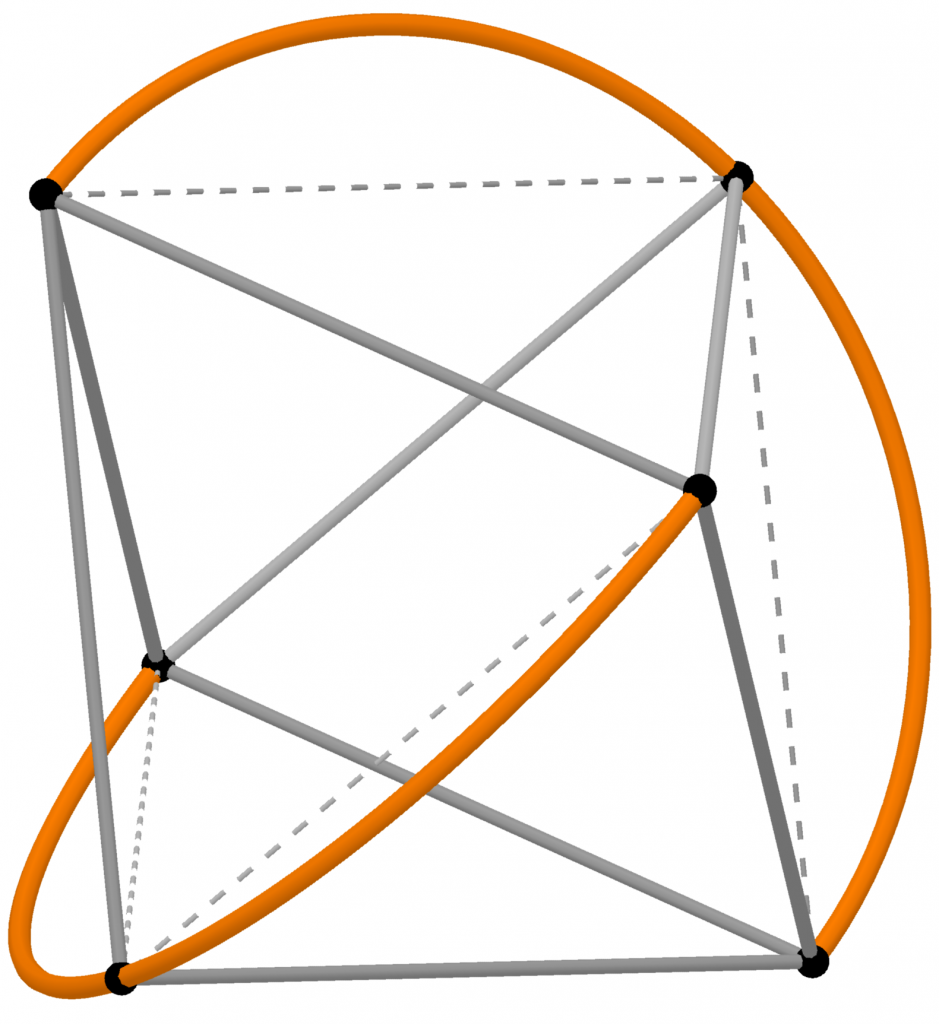
Sur le plan des mathématiques, le Grand Rampant est simple : imaginez un carré dans un plan horizontal, muni de ses deux diagonales. Tracez dans le demi-plan vertical du dessus le demi-cercle ayant pour diamètre la première diagonale. Tracez dans le demi-plan vertical du dessous le demi-cercle ayant pour diamètre la seconde diagonale. Les deux demi-cercles se trouvent donc dans des plans perpendiculaires entre eux, et perpendiculaires au plan du carré. L’objet peut aussi être vu comme les moitiés de deux grands cercles d’une même sphère, situés dans des plans perpendiculaires.
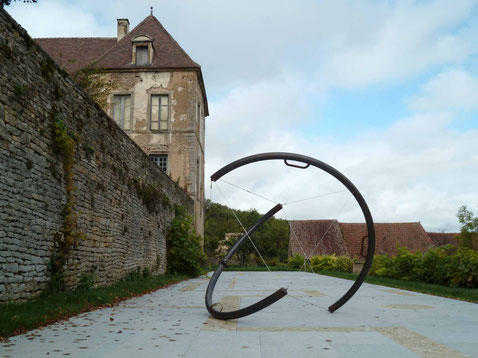 |
 |
Le Grand Rampant
Si conceptuellement le Grand Rampant est relativement simple, sa construction, elle, n’a pas dû être aisée ! Surtout pour le modèle réalisé à échelle humaine. Les demi-cercles sont des tubes en acier d’une dizaine de centimètres de diamètre, et ce qui est surprenant : huit haubans tendus suffisent à assurer la rigidité de l’ensemble ! Lorsqu’une structure avec un squelette est maintenue par la tension de filins, on parle en architecture ou en bio-mécanique de tenségrité. Comme indiqué sur la figure, ces câbles sont huit des douze arêtes d’un octaèdre régulier. Les demi-cercles sont munis de 2 poignées ou de 2 cale-pieds, de telle sorte qu’un humain (de la taille d’Ulysse) puisse se tenir dans l’objet et le mettre en mouvement. Le Grand Rampant utilisé par Ulysse au Palais de la découverte mesure 2,40 m de diamètre. Vous pouvez admirer divers Rampant (petits et grands) en mouvement sur le site de l’artiste 1.

Ulysse Lacoste en mouvement dans le Palais de la découverte.
La trace au sol de l’objet en mouvement a été marquée à la craie. À chaque instant, la sculpture prend appui sur l’extrémité du diamètre d’un des demi-cercles et sur un point de l’autre demi-cercle. Quand l’objet roule, les points de contact avec le sol sont donc les extrémités des génératrices d’un demi-cône. Puis les rôles s’échangent, et c’est le deuxième demi-cône dont les génératrices sont posées sur le sol. La trace obtenue dessine alors le patron de l’enveloppe convexe du Grand Rampant qui s’appelle un sphéricône.

Démonstration au Palais de la découverte.
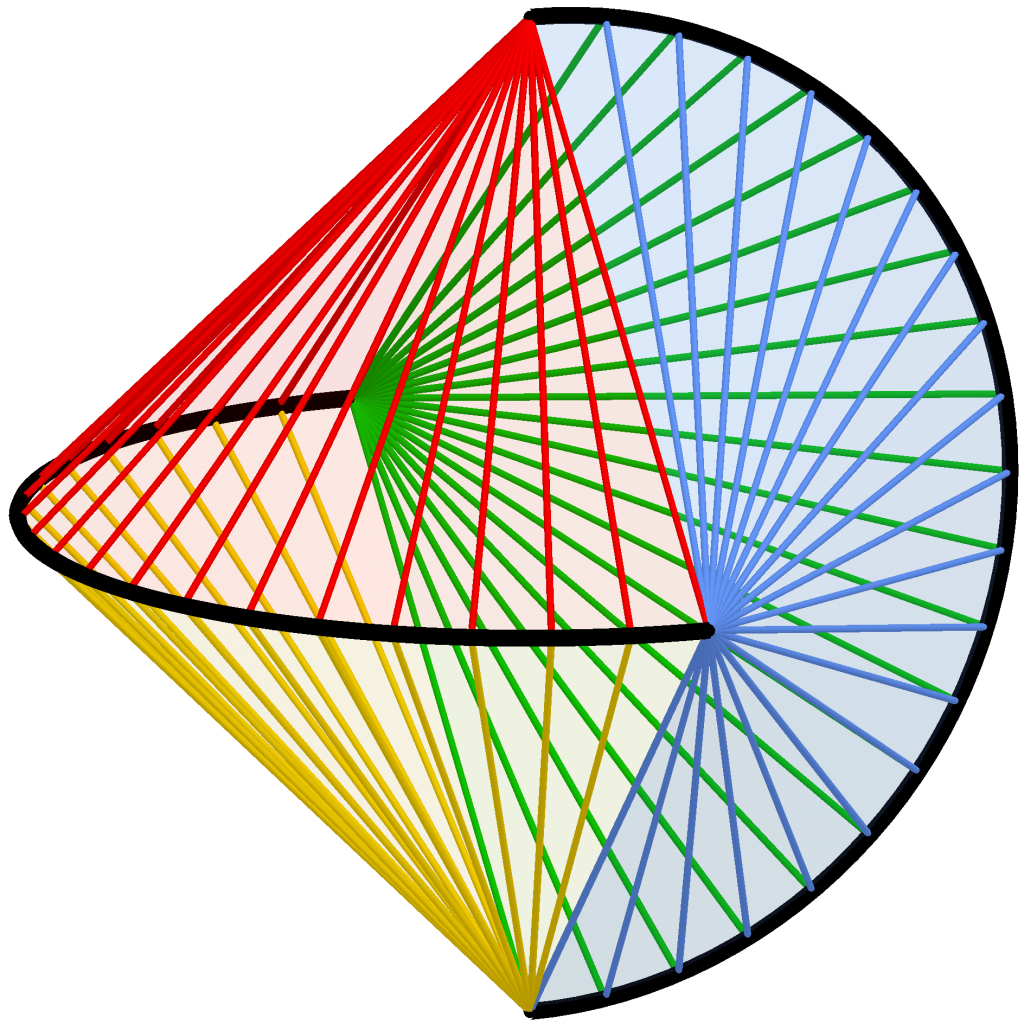
Le sphéricône et les demi-cônes.
La trace au sol est donc une esthétique succession d’arcs de cercles composant une sorte de feston. Penchons-nous d’un peu plus près sur ce feston. Pourquoi des arcs de cercles ?
Nommons \(T_1\) et \(T_2\) les deux tubes et \(D_1\) et \(D_2\) leurs diamètres. \(D_1\) et \(D_2\) sont les diagonales du carré de base et \(c\) le côté du carré. Chaque diamètre est perpendiculaire au plan de l’autre demi-cercle, et passe par son centre. Chacune de ses extrémités est donc à une même distance \(c\) de tout point de l’autre demi-cercle. Quand le mobile se déplace, l’extrémité d’un des demi-cercles est fixe, la trace au sol est donc composée d’arcs de cercle de rayon \(c\).
Quel est leur angle au centre ? Le tube roule sans glisser sur le sol. La longueur de la trace laissée est la longueur du tube, soit \(L = \pi c
\dfrac{\sqrt{2}}{2}\cdotp\) L’angle au centre \(\beta\) satisfait \(c \beta = \pi c
\dfrac{\sqrt{2}}{2}\), d’où \(\beta = \pi \dfrac{\sqrt{2}}{2}\cdotp\) Converti en degré, \(\beta\) vaut environ 127°.
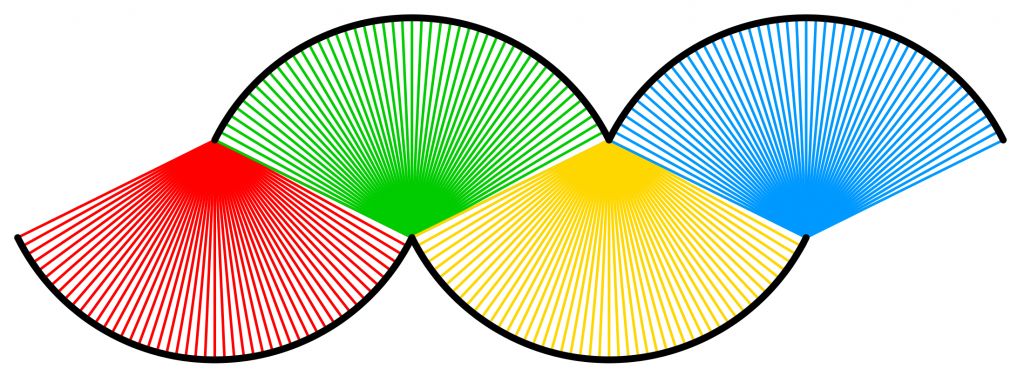
Trace des demi-cônes.
Je ne prétends pas que la pratique de l’objet soit aisée. Elle est en tout cas spectaculaire. Ulysse porte un casque, et se trouve alternativement la tête vers le bas, en appui sur le demi-cercle des mains et sur une position tête en haut, en appui sur le demi-cercle des pieds. Il prétend cependant que le maniement s’acquiert assez facilement et qu’il n’a pas été victime d’accident majeur en pratiquant son Grand Rampant.
À l’issue de la démonstration, Ulysse Lacoste proposait, en co-animation avec Robin Jamet, médiateur de mathématiques du Palais, un atelier de découverte de son art, où il a montré des maquettes et d’autres modèles de sculptures dont il nous a décrit la genèse.

D’autres objets surprenants.
Les sculptures mobiles ne sont qu’une partie du travail de cet artiste, créatif dans de nombreux domaines et qui pratique bien d’autres formes d’art. Mais, par le lien très fort qu’elles entretiennent avec la physique et la géométrie, elles en constituent un aspect auquel, en tant que professeurs de mathématiques, nous ne saurions rester indifférents !
Remarques : la version numérique de l’article vous permettra de mieux percevoir l’objet grâce aux figures animées réalisées par Vincent Pantaloni sous GeoGebra 3D ![]() . Les photos prises au Palais de la découverte sont de Roger Mansuy, les figures GeoGebra de l’article sont également de Vincent Pantaloni.
. Les photos prises au Palais de la découverte sont de Roger Mansuy, les figures GeoGebra de l’article sont également de Vincent Pantaloni.
-
 . ↩
. ↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Claudie Asselain-Missenard a pris une retraite méritée après de nombreuses années en poste dans l’académie de Versailles, puis celle de Paris. Membre active de l’APMEP, elle a co-dirigé la revue PLOT.

Une réflexion sur « Le Grand Rampant »
Les commentaires sont fermés.